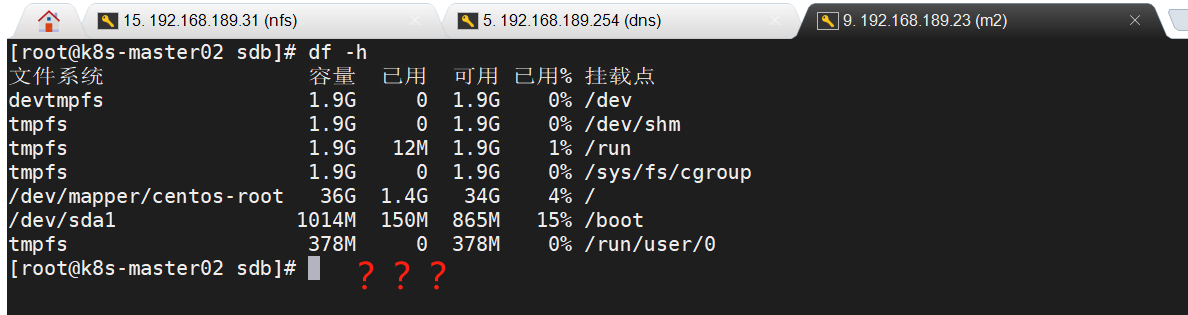
图的邻接矩阵存储
- 1)邻接矩阵表示法
- 相关概念
- 实现基础框架
- Graph_matrix
- 构造函数
- 实现基础操作
- 获取某一顶点的下标
- 添加边
- 打印邻接矩阵
- 2)BFS广度优先遍历
- 3)DFS深度优先遍历
- 4)最小生成树之克鲁斯卡尔算法
- 5)最小生成树之普里姆算法
- 6)单源最短路径之迪杰斯特拉算法
- 7)单源最短路径之贝尔曼福特算法
- 8)多源最短路径之弗洛伊德算法
1)邻接矩阵表示法
相关概念
- 如下图所示:适合存储稠密图,==O(1)==时间复杂度内判断两个顶点间的连接关系,并得到权值
实现基础框架
Graph_matrix
template <class V, class W, W MAX_W=INT_MAX, bool Direction = false>
//模板参数依次为:顶点、权重、是否有向
struct Graph_matrix{
public:
Graph_matrix() = default;
private:
vector<V> _vertex;
unordered_map<V, int> _indexMap; //顶点与下标的映射关系
vector<vector<W>> _matrix; //用顶点下标表示边的关系
};
构造函数
- 初始化_vertex顶点表,并记录顶点与下标的映射关系;初始化_matrix边矩阵
Graph_matrix(const V* _array, size_t n){
//初始化_vertex,记录各顶点与下标的映射关系
_vertex.reserve(n);
for (size_t i = 0; i < n; i++){
_vertex.push_back(_array[i]);
_indexMap[_array[i]] = i;
}
//初始化邻接矩阵
_matrix.resize(n);
for (size_t i = 0; i < n; i++){
_matrix[i].resize(n);
for (size_t j = 0; j < n; j++){
_matrix[i][j] = MAX_W;
}
}
}
实现基础操作
获取某一顶点的下标
size_t getVertexIndex(const V& v){
auto ret = _indexMap.find(v);
if (ret != _indexMap.end()){
return ret->second;
}
else{
return -1;
}
}
添加边
void addEdge(const V& src, const V& dst, const W& w){
int srcindex = getVertexIndex(src);
int dstindex = getVertexIndex(dst);
_matrix[srci][dsti] = w;
//无向图要处理对称的地方
if (Direction == false){
_matrix[dsti][srci] = w;
}
}
打印邻接矩阵
void print(){
for (auto e : _indexMap){
cout << e.first << "->" << e.second << endl;
}
cout << " ";
for (size_t i = 0; i < _vertex.size(); i++){
cout << i << " ";
}
cout << endl;
for (size_t i = 0; i < _matrix.size(); i++){
cout << i << " ";
for (size_t j = 0; j < _matrix[0].size(); j++){
if (_matrix[i][j] == MAX_W){
cout << "* ";
}
else{
cout << _matrix[i][j] << " ";
}
}
cout << endl;
}
}
2)BFS广度优先遍历
- 利用层次遍历 + 标记已访问过的顶点(已入队列)
//从某一顶点开始广度优先搜索
void BFS(const V& src){
size_t n = _vertex.size();
vector<bool> visited(n, false); //标记访问过的顶点
queue<V> qu;
int srci = getVertexIndex(src);
qu.push(srci);
visited[srci] = true;
while (!qu.empty()){
int cur = qu.front();
qu.pop();
cout << cur << "-> ";
for (size_t i = 0; i < n; i++){ //让src的邻接顶点依次入队
if (_matrix[cur][i] != MAX_W && visited[i] == false){
qu.push(i);
visited[i] = true;
}
}
}
}
3)DFS深度优先遍历
- 先访问src顶点并标记,然后找与src相邻且没有被访问过的顶点,递归
//从某一顶点开始深度优先搜索
void _DFS(int srci, vector<bool>& visited){
size_t n = _vertex.size();
cout << srci << "-> ";
visited[srci] = true;
//找与src相邻且没有被访问过的顶点,递归
for (size_t i = 0; i < n; i++){
if (_matrix[srci][i] != MAX_W && visited[i] == false){
_DFS(i, visited);
}
}
}
void DFS(const V& src){
int srci = getVertexIndex(src);
vector<bool> visited(_vertex.size(), false);
_DFS(srci, visited);
}
4)最小生成树之克鲁斯卡尔算法
查看克鲁斯卡尔算法的代码实现
5)最小生成树之普里姆算法
查看普里姆算法的代码实现
6)单源最短路径之迪杰斯特拉算法
查看迪杰斯特拉算法的代码实现
7)单源最短路径之贝尔曼福特算法
查看贝尔曼福特算法的代码实现
8)多源最短路径之弗洛伊德算法
查看弗洛伊德算法的代码实现









![[附源码]java毕业设计领导干部听课评课管理系统](https://img-blog.csdnimg.cn/623dfb74176e44a8915f06a72c96ea2f.png)
![P3205 [HNOI2010]合唱队](https://img-blog.csdnimg.cn/8f520dc1332045f7be8d9aad2709cd7c.png)