$\bullet$ 分类模型中除了贝叶斯决策规则，SVM，最近邻分类器，还有决策树
$\bullet$ 决策树就是选一个属性，根据属性的不同取值，将样本划分为不同的类，不断重复下去，直到终止。在叶子节点处，通过多数投票，赋予一个标签

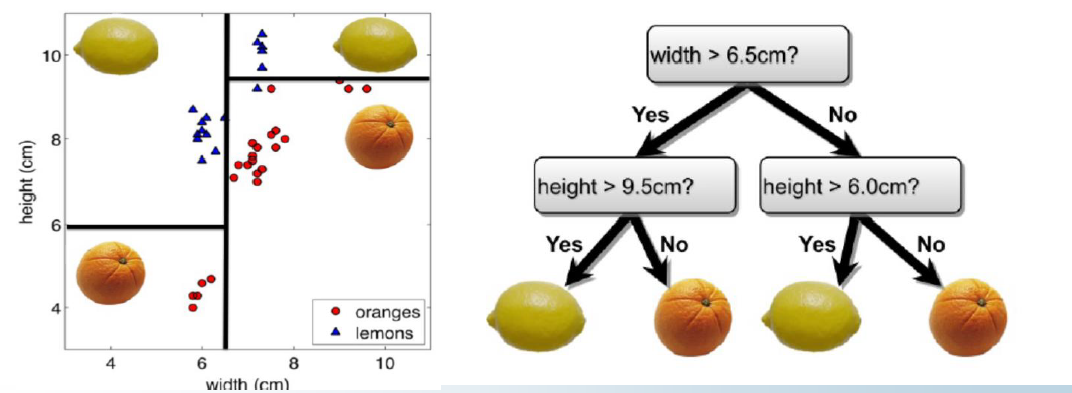
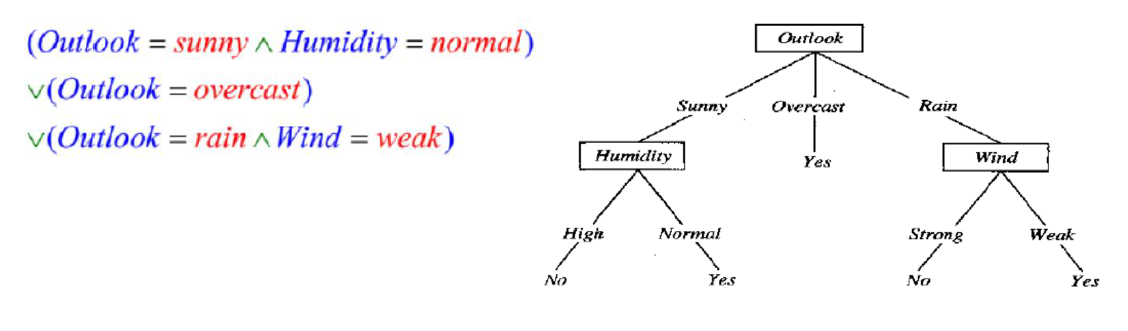
$\bullet$ 对于一个餐馆等餐问题



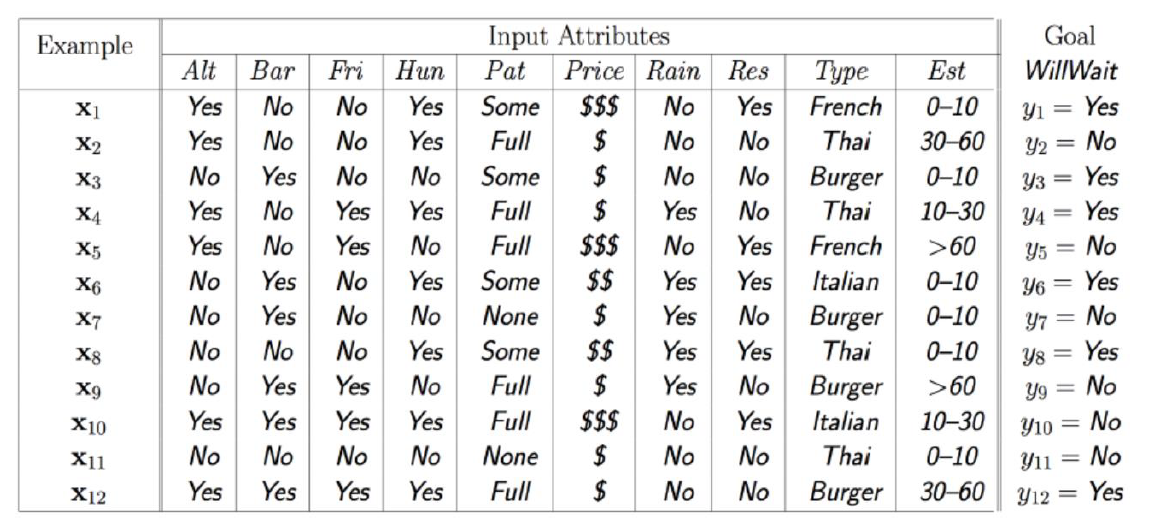
$\bullet$ 离散属性值天然适合分叉，比如对于性别，男女各为一类；而对于连续的属性值，可以考虑选择一些阈值，将连续值划分为多个取值空间，每个空间为一类，如上面的WaitEstimate
$\bullet$ 每个叶子节点就代表一个分类或者决策，也是一个rule
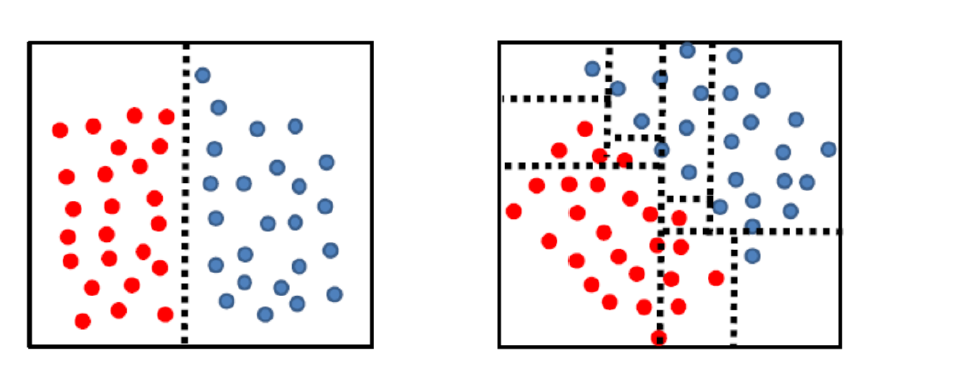
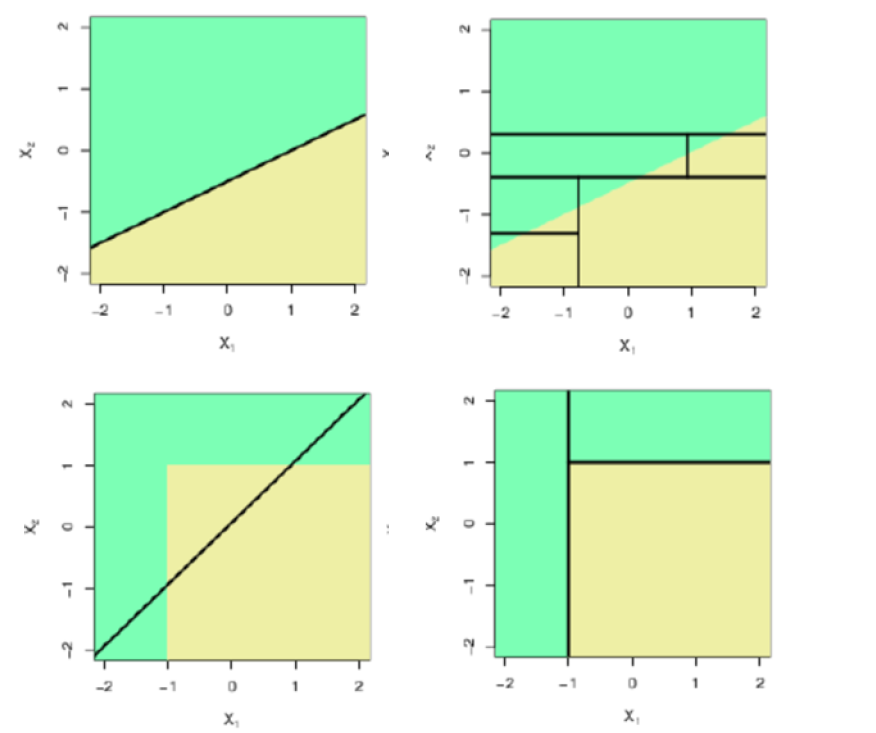
$\bullet$ 决策树将特征空间划分为一个个与坐标轴平行的矩形

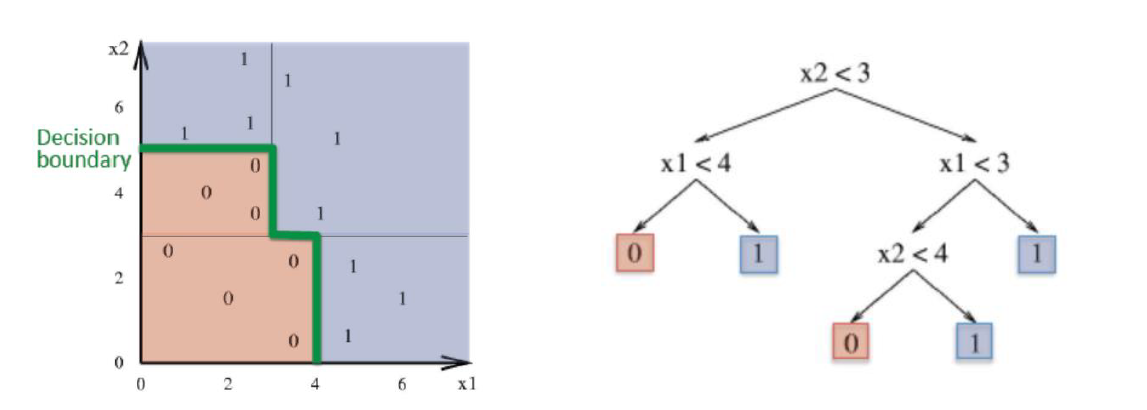
$\bullet$ 决策树的复杂度高度依赖于特征空间中样本的几何形状

$\bullet$ 有些样本用线性分类器很容易，用决策树却很费劲；而有些样本线性不可分，用决策树却几步就完成了。决策树分段线性，合起来就是非线性了。

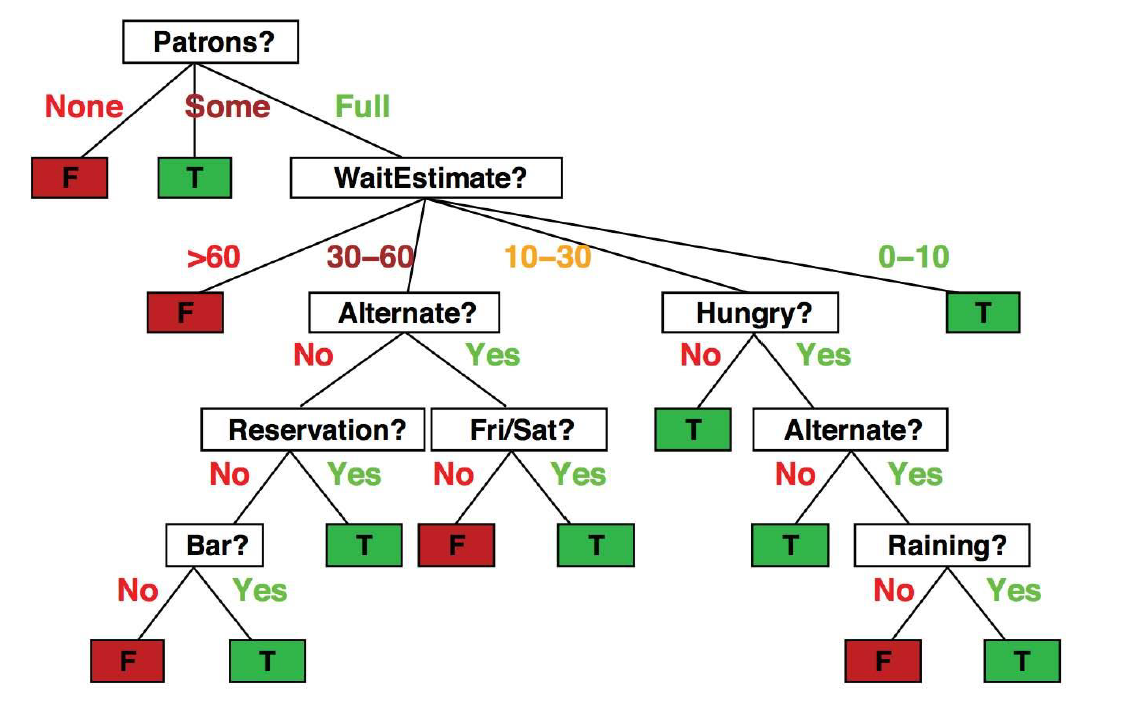
$\bullet$ 每一个叶子 产生一条规则，规则由根到该叶子的路径上所有节点的条件，规则的结论是叶子上标注的结论（决策，分类，判断）决策树规则 代表实例属性值约束的合取（交集）的析取（并集）式。从树根到树叶的每一条路径对应一组属性测试的合取 树本身对应这些合取的析取。下面给出Yes类的rules

$\bullet$ 分类树的叶子节点输出离散值，一般通过多数投票得到；回归树的叶子节点输出连续值，一般通过取均值得到
$\bullet$ 一些优缺点

• 解释性好，也更加符合人的决策方式。深度学习的一个为人诟病的点就是解释不了，你只知道最终分类的结果，但是不知道分类的依据，为什么这么分。在某些领域，如人脸识别，我们只关心是不是人脸，至于怎么分的我们不是很关心；但是如果在医疗诊断领域，机器判断出病人有癌症，但是依据是什么不知道，我们可能就无法接受了。
• 树可以用图来表示，形象直观，更加容易理解
• 构建树相对容易
• 对新样本进行分类时速度很快
• 分类精度比起其他分类器较低

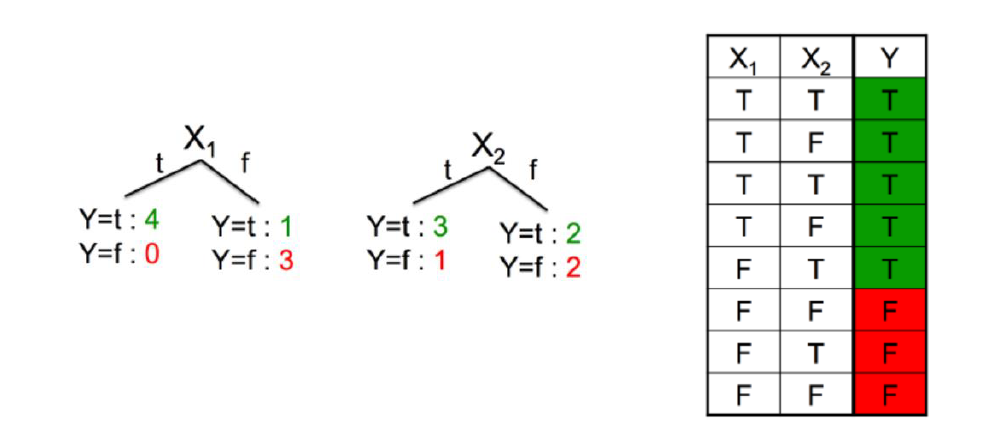
$\bullet$ 构建树的时候，我们关心在每个节点，选择什么样的属性来进行分叉。我们自然希望选一个“好”点的属性，能将样本尽可能地分开，那么如何衡量一个属性好不好呢？

$\bullet$ 直觉告诉我们属性$X_1$更好一些，因为分叉后，不确定性减少了。左边的全是正样本，而右边负样本的概率很大。衡量不确定性可以用熵
$$\begin{gathered} P\left(X=x_i\right)=p_i,i=1,2,\cdots ,n \\ H(X)=-\sum _{i=1}^n{p}_i\log p_i \end{gathered}$$
$\bullet$ 假如随机变量$X$只取两个值$0,1$
$$\begin{gathered} P(X=1)=p,P(X=0)=1-p,0⩽p⩽1 \\ H(p)=-p{\log }_{2}p-(1-p){\log }_2(1-p) \end{gathered}$$

$\bullet$ 可以想象，当一个随机变量取每一个值的概率都相等，其不确定性最大，熵最大
设有随机变量 $(X,Y)$, 其联合概率分布为

条件熵

$$P\left(X=x_i,Y=y_j\right)=p_{ij},i=1,2,\cdots ,n;j=1,2,\cdots ,m$$
条件樀 $H(Y\mid X)$ 表示在已知随机变量 $X$ 的条件下随机变量 $Y$ 的不确定性. 随机变 量 $X$ 给定的条件下随机变量 $Y$ 的条件熵 (conditional entropy) $H(Y\mid X)$, 定义为 $X$ 给定条件下 $Y$ 的条件概率分布的熵对 $X$ 的数学期望
$$\begin{gathered} H(Y\mid X)=\sum _{i=1}^n{p}_{i}H\left(Y\mid X=x_i\right) \\ {p}_i=P\left(X=x_i\right),i=1,2,\cdots ,n \end{gathered}$$
信息增益（information gain）表示得知特征 $X$ 的信息而使得类 $Y$ 的信息的不 确定性减少的程度.

信息增益

定义 (信息增益)： 特征 $A$ 对训练数据集 $D$ 的信息增益 $g(D,A)$, 定义为 集合 $D$ 的经验熵 $H(D)$ 与特征 $A$ 给定条件下 $D$ 的经验条件樀 $H(D\mid A)$ 之差, 即
$$g(D,A)=H(D)-H(D\mid A)$$
一般地, 熵 $H(Y)$ 与条件熵 $H(Y\mid X)$ 之差称为互信息 (mutual information). 决 策树学习中的信息增益等价于训练数据集中类与特征的互信息.

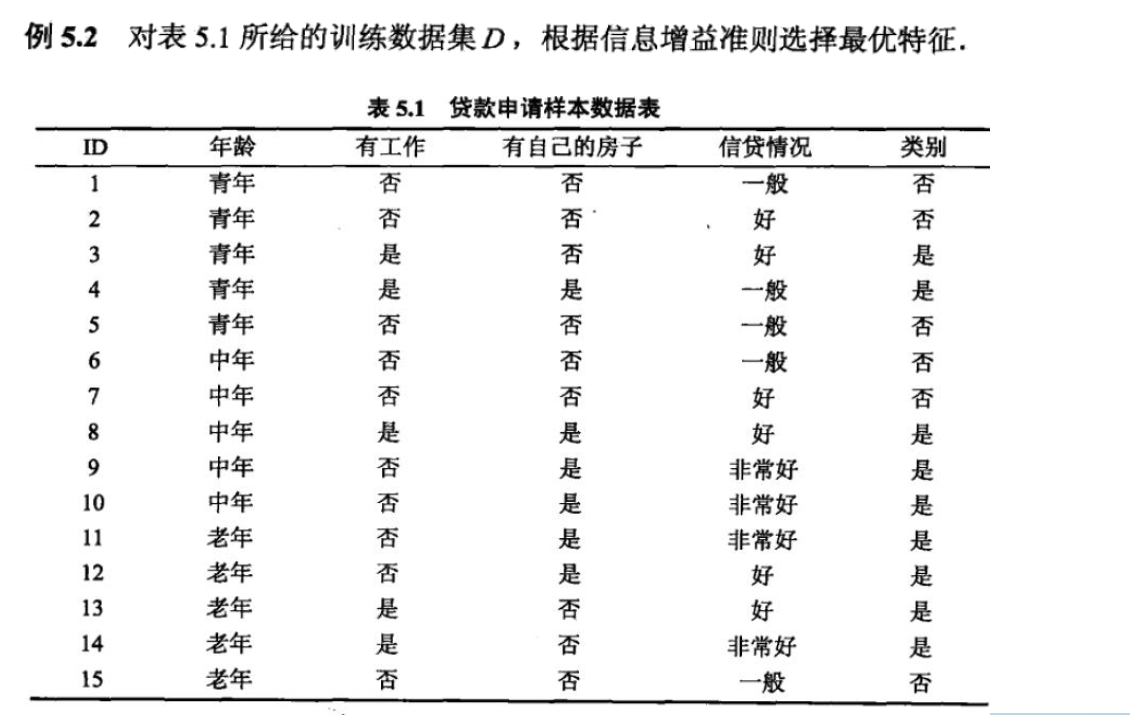
根据信息增益准则的特征选择方法是: 对训练数据集 (或子集) $D$, 计算其 每个特征的信息增益, 并比较它们的大小, 选择信息增益最大的特征.

算法 (信息增益的算法)
输入: 训练数据集 $D$ 和特征 $A$;
输出：特征 $A$ 对训练数据集 $D$ 的信息增益 $g(D,A)$.

1. 计算数据集 $D$ 的经验熵 $H(D)$
   $$H(D)=-\sum _{k=1}^K\frac{\left|C_k\right|}{|D|}{\log }_2\frac{\left|C_k\right|}{|D|}$$

2. 计算特征 $A$ 对数据集 $D$ 的经验条件樀 $H(D\mid A)$
   $$H(D\mid A)=\sum _{i=1}^n\frac{\left|D_i\right|}{|D|}H\left(D_i\right)=-\sum _{i=1}^n\frac{\left|D_i\right|}{|D|}\sum _{k=1}^K\frac{\left|D_{ik}\right|}{\left|D_i\right|}{\log }_2\frac{\left|D_{ik}\right|}{\left|D_i\right|}$$

3. 计算信息增益
   $$g(D,A)=H(D)-H(D\mid A)$$

$\bullet$ $H(D)$代表原来的不确定性，$H(D|A)$代表用属性$A$进行分叉后的不确定性，两个相减就是用属性$A$进行分叉可以减少的不确定性，也叫信息增益。条件熵我是这么理解的，属性将样本分为几个类，每个类都有一个概率（类样本除总样本），每一类都有一个熵（计算方法和$H(D)$一样），条件熵是每个类的熵乘每个类的概率，最后求和