计数质数
描述 :
给定整数 n ,返回 所有小于非负整数 n 的质数的数量 。
题目 :
LeetCode 204.计数质数 :
204. 计数质数

分析 :
解决这个题有一个有效的方法,叫埃氏筛 , 后来又产生了线性筛,奇数筛等改进的方法。
基本思想是如果 x是质数,那么大于 的 xy 的倍数 2x.3x..一定不是质数,因此我们可以从这一点入手。如下图所示:
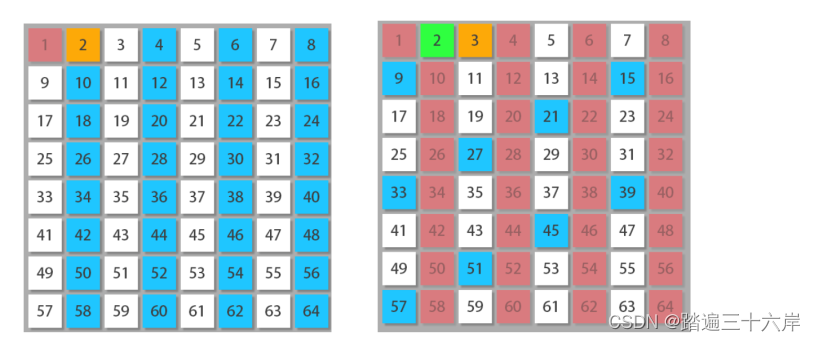
我们先选中数字2,2是素数,然后将2的倍数全部排除 (在数组里将该位置标记为0就行了)
接着我们选中数字3,3是素数,然后将3的倍数全部排除
接着我们选择数字5,5是素数,然后将5的倍数全部排除。
接着我们选择 7,11,13一直到 n,为什么 4、6、8、9 ...不会再选择了呢? 因为我们已经在前面的步骤中,将其变成0了。所以实现代码如下:
解析 :
class Solution {
public int countPrimes(int n) {
if(n <= 1){
return 0;
}
int count = 0;
int[] arr = new int[n];
Arrays.fill(arr,1);
for(int i = 2 ;i < n ;i++){
if(arr[i] == 1){
count++;
if((long) i * i < n){
for(int j = i * i ; j < n;j += i){
arr[j] = 0;
}
}
}
}
return count;
}
}这期就到这里 , 下期见!