两个字符串的最小ASCLL删除和

力扣链接

求 删除字符的ASCLL和的最小值 ⇒ 正难则反 ⇒ 求公共子序列的ASCLL和的最大值

• 两个数组的dp问题 ⇒ 分区间讨论 ⇒ dp[i][j] -- nums1数组的[0, i] 区间 和 nums2数组的[0, j] 区间, 公共子序列的ASCLL和的最大值

• 转态转移方程 — 根据最后一个位置进行讨论
  

• 遍历顺序
  

• 初始化
  需要使用左上角的情况 ⇒ dp表可以多开一行, 多开一列
  但是dp表中使用原 nums1 和 nums2的情况就会出现偏差, 解决方法

  1. 访问nums1 和 nums2里面的情况, 就要 －1
  2. 可以在nums1, nums2前面添加一个 空格 ⇒ 使得dp表中的下标 和 nums1 和 nums2中的下标一致化

  ⇒ 这样初始化就方便很多 , 都初始化为 0

• 返回值— dp[i][j] -- nums1中的[0, i] 区间 以及 nums2中的 [0, j]区间内的所有子序列的组合中, 公共子序列的最大长度 ⇒ 返回 两个数组和 - 2 * dp[m][n]

class Solution {
public:
    int minimumDeleteSum(string s1, string s2) 
    {
        int m = s1.size();
        int n = s2.size();

        vector<vector<int>> dp(m+1, vector<int>(n+1));

        int sum = 0;
        for(auto e : s1)  sum += e;
        for(auto e : s2)  sum += e;
        
        for(int i = 1; i <=  m; i++)
        {
            for(int j = 1; j <= n; j++)
            {
                if(s1[i-1]  == s2[j-1])
                {
                    dp[i][j]  = dp[i-1][j-1] + s1[i-1];
                }
                else
                {
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
                }
            }
        }

        int res  = sum - 2 * dp[m][n];

        return res;
    }
};

---

最长重复子数组

力扣链接

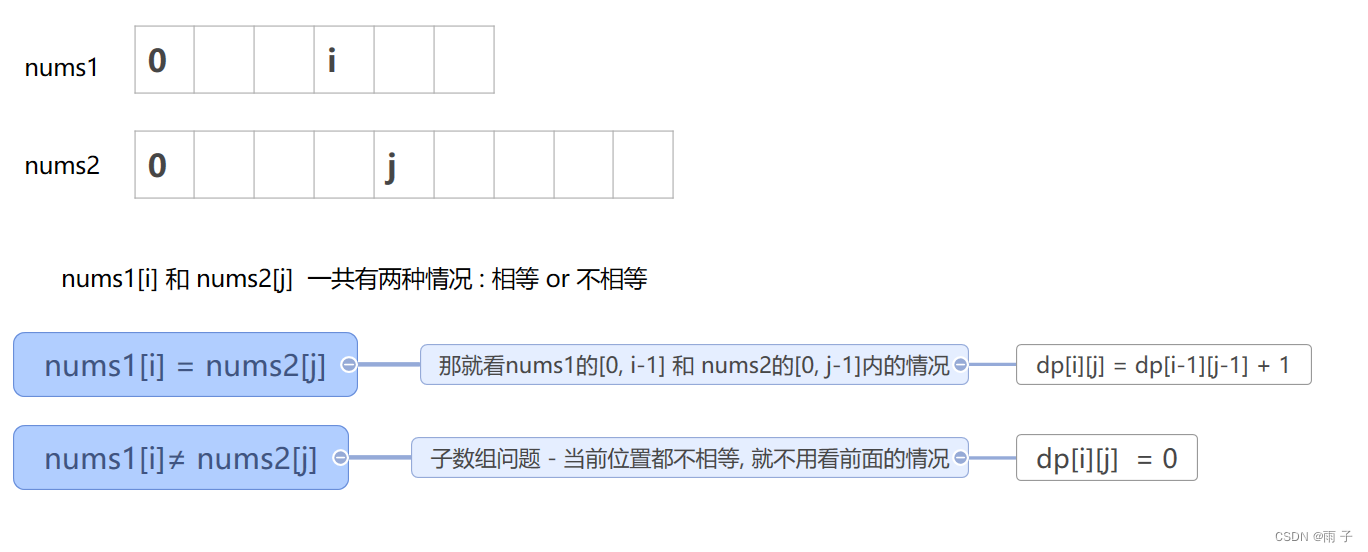
• 两个1数组的dp问题(子数组) — 每个数组的结束位置进行讨论 ⇒ dp[i][j] -- nums1数组中以nums1[i]结尾的子数组中 和 nums2数组中以nums2[j]结尾的子数组中, 公共子数组的最长长度

• 状态转移方程
  

• 遍历顺序
  

• 初始化
  需要使用左上角的情况 ⇒ dp表可以多开一行, 多开一列
  但是dp表中使用原 nums1 和 nums2的情况就会出现偏差, 解决方法

  1. 访问nums1 和 nums2里面的情况, 就要 －1
  2. 可以在nums1, nums2前面添加一个 空格 ⇒ 使得dp表中的下标 和 nums1 和 nums2中的下标一致化

  ⇒ 这样初始化就方便很多 , 都初始化为 0

• 返回结果 — 返回dp表中的最大值

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) 
    {
        int m = nums1.size();
        int n = nums2.size();

        vector<vector<int>> dp(m+1, vector<int>(n+1));

        int res = 0;
        for(int i = 1; i <= m; i++)
        {
            for(int j = 1; j <= n; j++)
            {
                if(nums1[i-1] == nums2[j-1])
                {
                    dp[i][j] = dp[i-1][j-1] + 1;
                }

                res = max(res, dp[i][j]);
            }
        }

        return res;
    }
};

---

云锁断崖无觅处，半山松竹撼秋风. —— 岳飞