目录
- 1.概述
- 1.1.Boyer-Moore 算法介绍
- 1.2.坏字符规则表
- 1.3.好后缀规则表
- 1.4.总结
- 2.代码实现
- 3.应用
更多数据结构与算法的相关知识可以查看数据结构与算法这一专栏。
有关字符串模式匹配的其它算法:
【算法】Brute-Force 算法
【算法】KMP 算法
【算法】Rabin-Karp 算法
1.概述
1.1.Boyer-Moore 算法介绍
(1)Boyer-Moore 算法又称为 Boyer-Moore 字符串搜索算法(下文简称为 BM 算法),由 Robert S. Boyer 和 J Strother Moore 于1977年提出,它是一种高效的字符串匹配算法,用于在一个目标串中查找一个模式串的出现位置。它的核心思想是通过预处理模式串,利用字符比较的不匹配信息来跳过尽可能多的目标字符,从而快速定位可能的匹配位置,以减少比较次数。
(2)BM 算法的主要思想是从模式串(要搜索的字符串)的末尾开始匹配,然后根据不匹配字符在模式串中的位置,跳过一些不必要的比较。具体来说,BM 算法通过预处理模式串,构建两个表:
- 坏字符规则表:用于记录模式串中每个字符的最后出现位置。在匹配过程中,当发生不匹配时,根据坏字符规则表决定将模式串向右滑动
badShift位。 - 好后缀规则表:记录模式串中每个后缀子串的匹配长度。当模式串的后缀子串与主串的某个子串匹配时,可以使用好后缀规则表决定将模式串向右滑动
goodShift位。
当发生不匹配时,模式串向右滑动的位数为 max(badShift, goodShiftf)。下面将具体介绍这两种规则表。
1.2.坏字符规则表
(1)当目标串中的某个字符跟模式串的某个字符不匹配时,我们称目标串中的这个不匹配字符为坏字符,此时模式串需要向右移动 badShift 位,并且 badShift = 当前对比的字符在模式串中的位置 - 坏字符在模式串中最右出现的位置,如果该模式串中不存在该坏字符,那么最右出现的位置设置为 -1。例如,在下图中,从模式串的末尾开始匹配,显然字符 F 与 字符 B 不匹配,因此字符 F 便为坏字符。
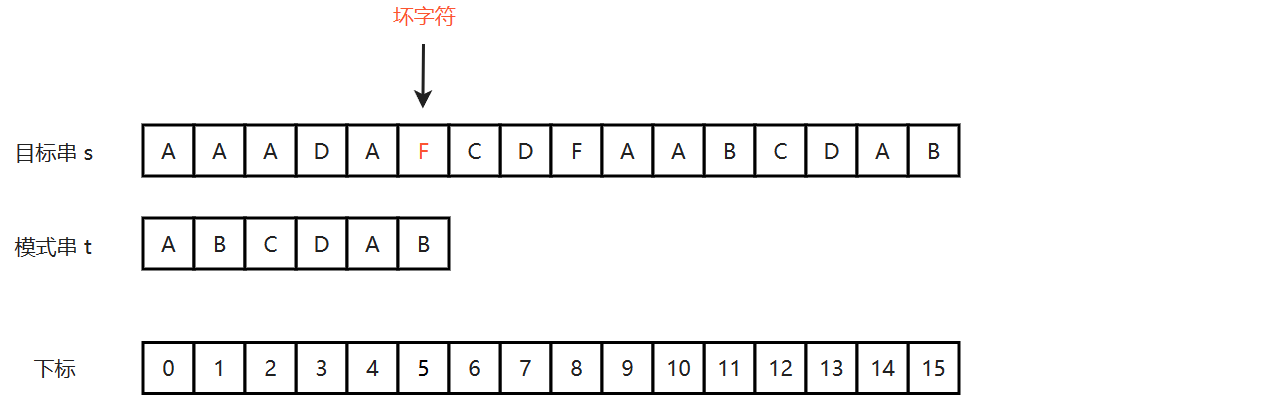
(2)而上面模式串中并没有字符 F,因此由上面的公式可得 badShift = 5 - (-1) = 6,如下图所示:
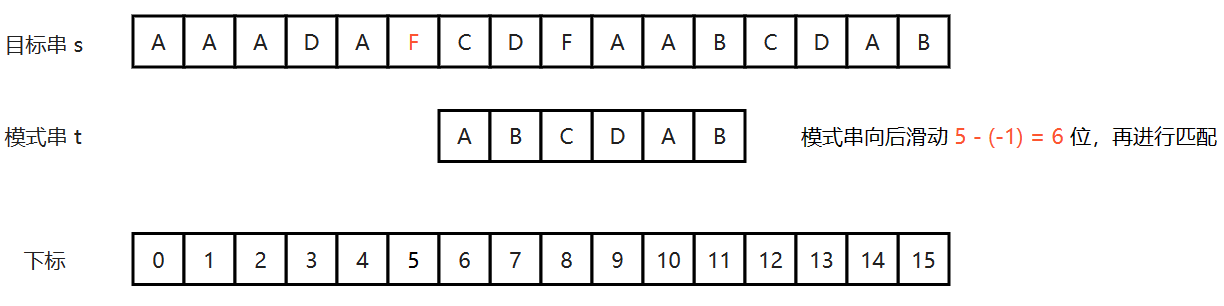
(3)之所以在遇到坏字符时模式串需要向后移动 badShift 位,其原因在于对于当前坏字符来说:
- 如果模式串中没有该坏字符,那么说明模式串中的任何一个字符都不可能与其匹配成功,所以此时模式串的第一个字符应该直接目标串中该坏字符的后一个字符对齐,即上图中模式串中的字符 A 与目标串中的字符 C 对齐,然后再进行匹配;
- 如果模式串中有该坏字符,我们需要选取模式串中最右出现的该坏字符,并且将它们对齐。之所以要选取最右字符,其原因在于防止漏掉正确答案,具体例子如下:



(4)在代码实现中,我们可以用数组来存储模式串中每个字符最右出现的下标,并且模式串中不存在的字符的下标默认为 -1。而坏字符规则表的大小一般为 256,其原因在于在 ASCII 编码中,总共有 256 个字符,每个字符的取值范围是 0 - 255。通过使用 256 大小的坏字符规则表,可以覆盖所有可能的字符。
1.3.好后缀规则表
(1)在 BM 算法中,好后缀是指在模式串中与主串匹配的后缀子串,例如下图中的 “ABC” 即为好后缀。

(2)而好后缀规则表 goodTable 一般用数组表示,其长度等于模式串的长度(记为 m),并且 goodTable[i] 表示好后缀 t[i + 1…m - 1] 的后缀子串能够匹配模式串中的其它最长子串 substring 时,模式串需要移动的位数,我们需要注意:
- 如果是好后缀本身与 substring 匹配,那么对 substring 没有什么限制(当然不能是好后缀本身),但是当存在多个匹配的 substring 时,我们应该选择最右出现的 substring,其理由与上面类似,主要是为了防止漏掉正确答案。
- 如果是好后缀的后缀子串且不是好后缀本身与 substring 匹配,那么 substring 必须是模式串的前缀子串,其原因在于如果 substring 不是前缀子串(它一定是最长的),那么它的前一个字符必然和与其匹配的后缀子串的前一个字符不相等,这样一来滑动到当前位置的模式串就没有匹配的必要了。
例如,上图中好后缀 “ABC” 以及其后缀子串指 “ABC”、“C”、“BC” 这三个字符串,那么显然它们能够匹配模式串的其它最长子串为 “BC”(由于是后缀子串 “BC” 进行匹配的,因此 “BC” 必须是模式串的前缀子串),即 goodTable[3] = 5(此处的下标 3 对应模式串中的字符 D 的下标),如下图所示:

再例如,下图中好后缀 “ABC” 显然可以与模式串中的最长子串 “ABC”(绿色填充部分)匹配,即 goodTable[3] = 3(此处的下标 3 对应模式串中的字符 C 的下标)。


(3)虽然可以直接使用 goodTable 记录遇到好后缀时模式串需要移动的位数(其代码实现如下),但是求解 goodTable 的时间复杂度却达到了 O(n3)(两层 for 循环加上 equals 方法),这样一来效率较低。
public int[] getGoodTable(String t) {
int m = t.length();
int[] goodTable = new int[m];
Arrays.fill(goodTable, m);
for (int i = 1; i < m; i++) {
// suffix 为好后缀 t[i...m - 1]
String suffix = t.substring(i);
// suffix 长度
int suffixLen = m - i;
for (int j = m - 1; j >= m - suffixLen; j--) {
if (j >= suffixLen) {
//判断好后缀本身是否与其它子串匹配
if (t.substring(j - suffixLen, j).equals(suffix)) {
goodTable[m - i - 1] = m - j;
break;
}
} else {
//判断好后缀的后缀子串是否与前缀子串匹配
if (t.substring(0, j).equals(suffix.substring(suffixLen - j))) {
goodTable[m - i - 1] = m - j;
break;
}
}
}
}
return goodTable;
}
(4)实际上,我们可以使用另一种方法将时间复杂度降低到 O(n2),我们可以使用长度为 m 的数组 suffix 来保存每个不同长度的好后缀匹配的其它最长靠右子串的起始位置,以模式串 t = “ABCDABC” 为例:
| 好后缀 | 长度 | suffix | 解释 |
|---|---|---|---|
| C | 1 | suffix[1] = 2 | 长度为 1 的好后缀 C 与起始下标为 2 的子串 C 匹配,并且满足最长和靠右这两个要求 |
| BC | 2 | suffix[2] = 1 | 长度为 2 的好后缀 BC 与起始下标为 1 的子串 BC 匹配,并且满足最长和靠右这两个要求 |
| ABC | 3 | suffix[3] = 0 | 长度为 3 的好后缀 ABC 与起始下标为 0 的子串 BC 匹配,并且满足最长和靠右这两个要求 |
| DABC | 4 | suffix[4] = -1 | 好后缀 DABC 不与任何其它子串匹配,标记为 -1 |
| CDABC | 5 | suffix[5] = -1 | 好后缀 CDABC 不与任何其它子串匹配,标记为 -1 |
| BCDABC | 6 | suffix[6] = -1 | 好后缀 BCDABC 不与任何其它子串匹配,标记为 -1 |
求解数组 suffix 的代码如下,其时间复杂度为 O(n2)。
int m = t.length();
int[] suffix = new int[m];
Arrays.fill(suffix, -1);
for (int i = 0; i < m - 1; i++) {
int j = i;
int k = 0;
while (j >= 0 && t.charAt(j) == t.charAt(m - 1 - k)) {
j--;
k++;
suffix[k] = j + 1;
}
}
(5)如果我们通过数组 suffix 知道了当前好后缀并不能匹配其它子串时,那么如何判断它的后缀子串是否可以与模式串的前缀子串进行匹配呢?其实,解决办法也比较简单:
- 如果
suffix[k] != -1,那么说明当前好后缀t[j + 1...m - 1]可以匹配其它最长靠右子串,并且该子串的起始位置为suffix[k],此时模式串需要向右移动goodShift = j - suffix[k] + 1位,其中 j 与好后缀长度 k 的关系为k = m - 1 - j; - 如果
suffix[k] == -1,那么说明当前好后缀t[j + 1...m - 1]没有可以匹配的其它最长靠右子串,此时,我们需要从该好后缀的最长后缀子串t[r...m - 1]开始遍历(其中r = j + 2),寻找与之匹配的最长前缀。判断方法也比较简单,即判断suffix[m - r]是否为 0 即可:- 如果
suffix[m - r] == 0,则说明该后缀子串与长度为m - r前缀的匹配,此时模式串需要向右移动goodShift = r位; - 如果
suffix[m - r] != 0,则说明该后缀子串与长度为m - r前缀的不匹配,判断下一个后缀子串即可;
- 如果
- 如果上面两种情况都没有匹配成功,则直接返回模式串的长度,具体代码如下所示:
private static int moveByGs(int j, int m, int[] suffix) {
// k 为当前好后缀 t[j + 1...m - 1] 的长度
int k = m - 1 - j;
if (suffix[k] != -1) {
//好后缀可以直接匹配
return j - suffix[k] + 1;
}
//好后缀不能直接匹配,那么寻找与好后缀的后缀子串匹配的模式串的最长前缀
for (int r = j + 2; r <= m - 1; r++) {
//判断后缀子串 t[r...m - 1] 匹配的最长靠右子串的起始位置是否为 0
if (suffix[m - r] == 0) {
return r;
}
}
//上面两种情况都没有匹配成功,则直接返回模式串的长度
return m;
}
1.4.总结
在匹配过程中发生不匹配时,我们可以根据上面计算得到的坏字符规则表和好后缀规则表,来分别计算模式串应该向右滑动的最大位数 badShift 和 goodShift,并且都能保证不会漏掉正确答案。所以在 BM 算法中,每次发生不匹配时,模式串最终向右滑动的位数为 max(badShift, goodShift),即两者之间的最大值。
2.代码实现
(1)BM 算法的代码实现如下:
class BmAlgorithm {
private final static int ASCII_SIZE = 256;
public static int bmSearch(String s, String t) {
int n = s.length();
int m = t.length();
if (m == 0) {
return 0;
}
//坏字符规则表 badTable: 记录模式串中每个字符最后出现的位置
int[] badTable = new int[ASCII_SIZE];
Arrays.fill(badTable, -1);
for (int i = 0; i < t.length(); i++) {
badTable[t.charAt(i)] = i;
}
/*
* 好后缀规则表 goodTable: 用数组 suffix 表示
* suffix[i] 表示长度为 i 的好后缀匹配的最长靠右子串的起始位置
* */
int[] suffix = new int[m];
Arrays.fill(suffix, -1);
for (int i = 0; i < m - 1; i++) {
int j = i;
int k = 0;
while (j >= 0 && t.charAt(j) == t.charAt(m - 1 - k)) {
j--;
k++;
suffix[k] = j + 1;
}
}
int i = 0;
while (i <= n - m) {
//从右往左开始匹配
int j = m - 1;
while (j >= 0 && t.charAt(j) == s.charAt(i + j)) {
j--;
}
if (j < 0) {
//匹配成功
return i;
} else {
//根据坏字符规则计算要移动的位数
int badShift = j - badTable[s.charAt(i + j)];
//根据好字符规则计算要移动的位数
int goodShift = 0;
//如果 j == m - 1,即好后缀为 "",此时需要遵循坏字符规则
if (j < m - 1) {
goodShift = moveByGs(j, m, suffix);
}
i += Math.max(badShift, goodShift);
}
}
//无法匹配
return -1;
}
private static int moveByGs(int j, int m, int[] suffix) {
// k 为当前好后缀 pattern[j + 1...m - 1] 的长度
int k = m - 1 - j;
if (suffix[k] != -1) {
//好后缀可以直接匹配
return j - suffix[k] + 1;
}
//好后缀不能直接匹配,那么寻找与好后缀的后缀子串匹配的模式串的最长前缀
for (int r = j + 2; r <= m - 1; r++) {
//判断后缀子串 pattern[r...m - 1] 匹配的最长靠右子串的起始位置是否为 0
if (suffix[m - r] == 0) {
return r;
}
}
//上面两种情况都没有匹配成功,则直接返回模式串的长度
return m;
}
}
(2)测试代码如下:
class BmAlgorithmTest {
public static void main(String[] args) {
String text = "hello world AABCABC";
String pattern = "ABCDABC";
int index = bmSearch(text, pattern);
if (index != -1) {
System.out.println("Pattern found at index: " + index);
} else {
System.out.println("Pattern not found.");
}
}
}
输出结果为:
Pattern found at index: 16
注意:如果想找出所有匹配成功的位置,只需要简单改一下上面的代码即可,当匹配成功时,我们可以使用 list 来存储当前匹配成功的位置,当匹配结束后,返回 list 即可。
3.应用
BM 算法适用于各种类型的字符串匹配问题,具体来说,BM算法在以下情况下表现优秀:
- 目标串较长:BM 算法适用于处理大规模文本串的情况,因为它能够利用坏字符规则和好后缀规则在较少的比较操作中快速跳过大量的字符。
- 模式串较短:相对于文本串,模式串较短的情况下,BM 算法的性能更为突出,因为它能够利用坏字符规则和好后缀规则快速跳过无需比较的部分。
- 重复字符较少:如果模式串中包含大量重复字符,BM 算法的好后缀规则会出现退化的情况,导致性能下降。因此,当模式串中的重复字符较少时,BM算法能够发挥最佳性能。
总之,BM算法适用于大规模文本串和较短、重复字符较少的模式串的字符串匹配问题。它在实际中被广泛应用于文本编辑器、搜索引擎、数据处理等领域。