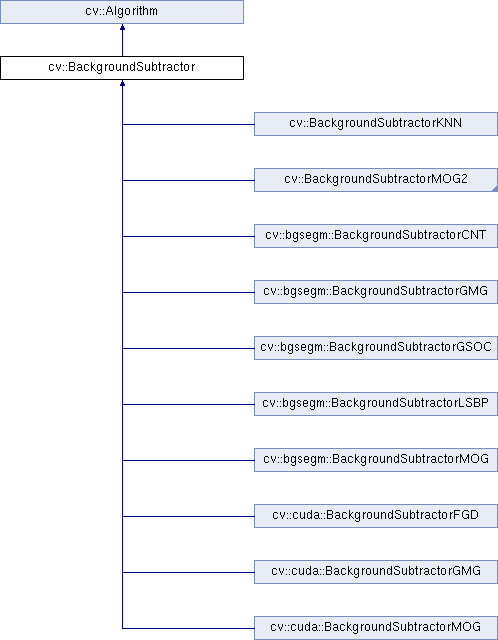
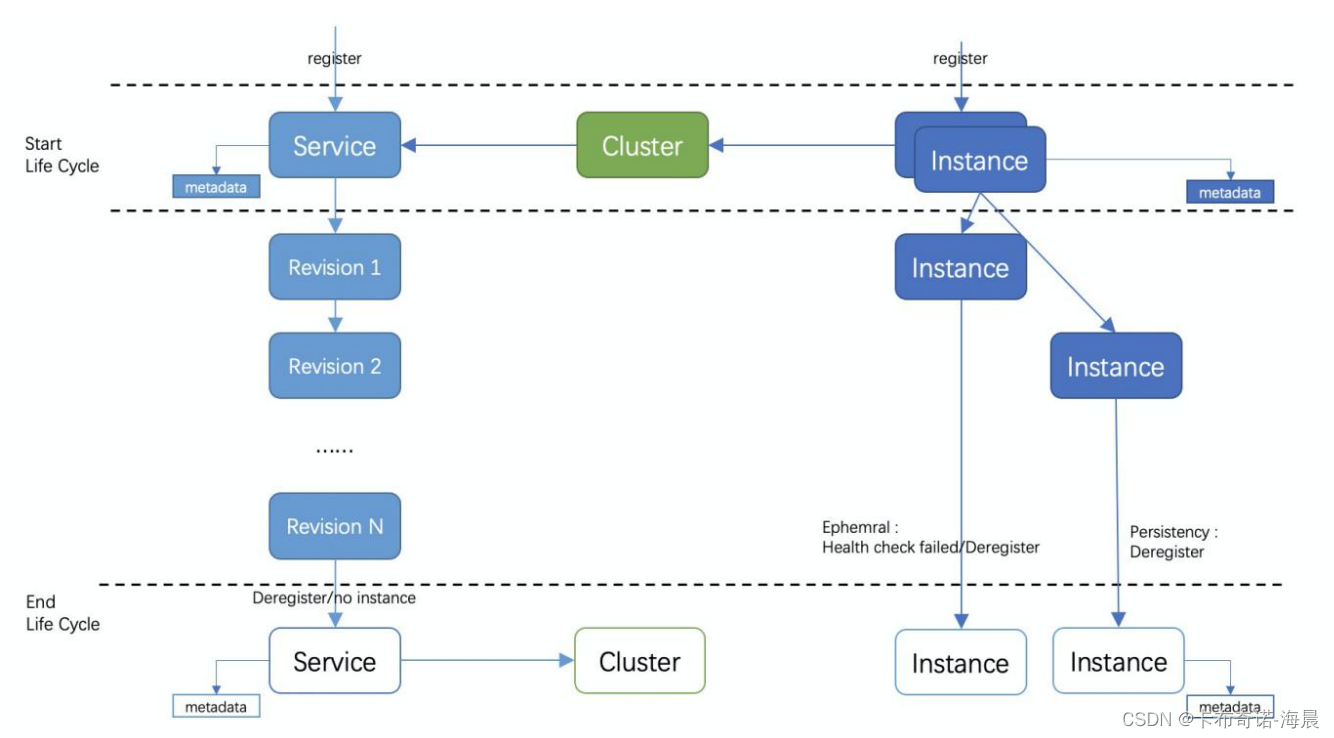
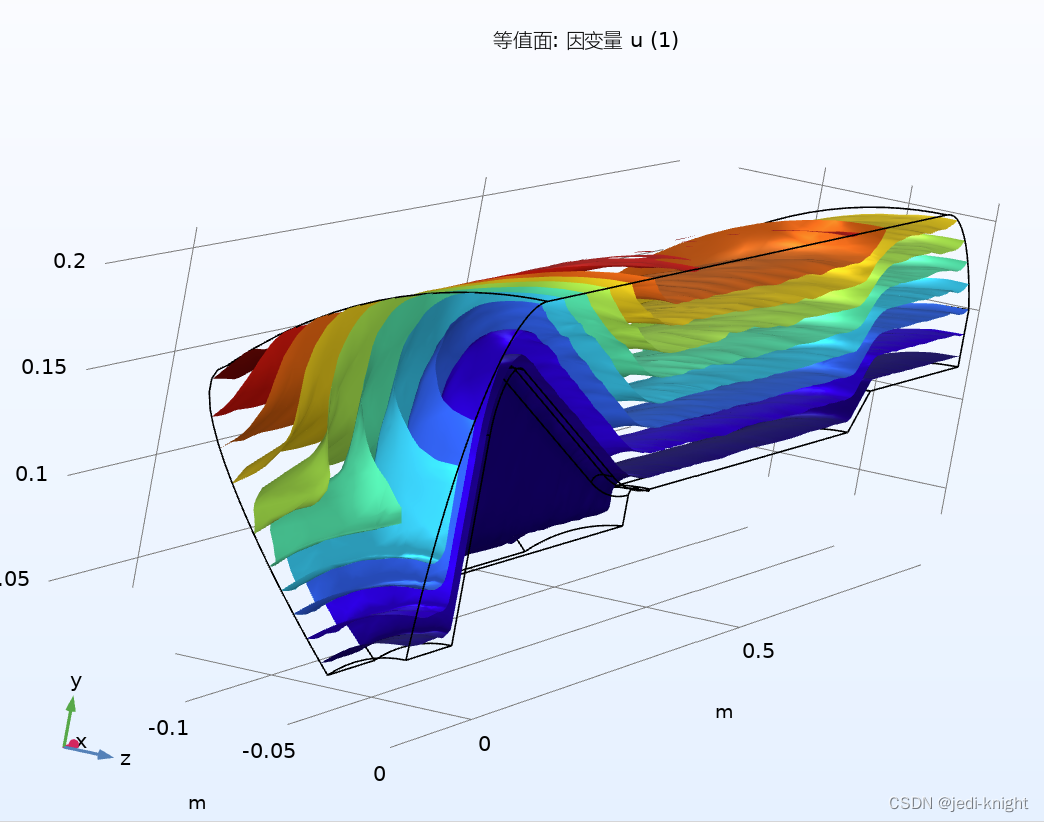
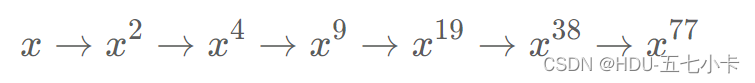09Shading3着色(插值、高级纹理映射)
- 1.Barycentric Coordinates 重心坐标
- 1.A点自己的重心坐标
- 2.如何求出任意点的重心坐标?
- 2.如何把纹理应用在实际的渲染中?Applying Textures
- 3.Texture Magnification纹理放大。(解决纹理小的问题)
- 双线性差值Bilinear Interpolation:做了两趟差值,水平一趟竖直一趟。
- 4.Texture Magnification (hard case) 如果纹理太大怎么办?
- Mipmap范围查询
- Trilinear Interpolation三线性差值
- 各向异性(在不同的方向上表现各不相同)过滤
1.Barycentric Coordinates 重心坐标
为了做三角形内部的差值而引入,希望通过三角形的顶点对三角形内部某一个值都能有一个平滑的过渡。
What do we want to interpolate?差值能做什么?
• Texture coordinates, colors, normal vector 可以差值纹理坐标,颜色,法向量
重心坐标是定义在三角形上的,一个三角形有一个重心坐标。
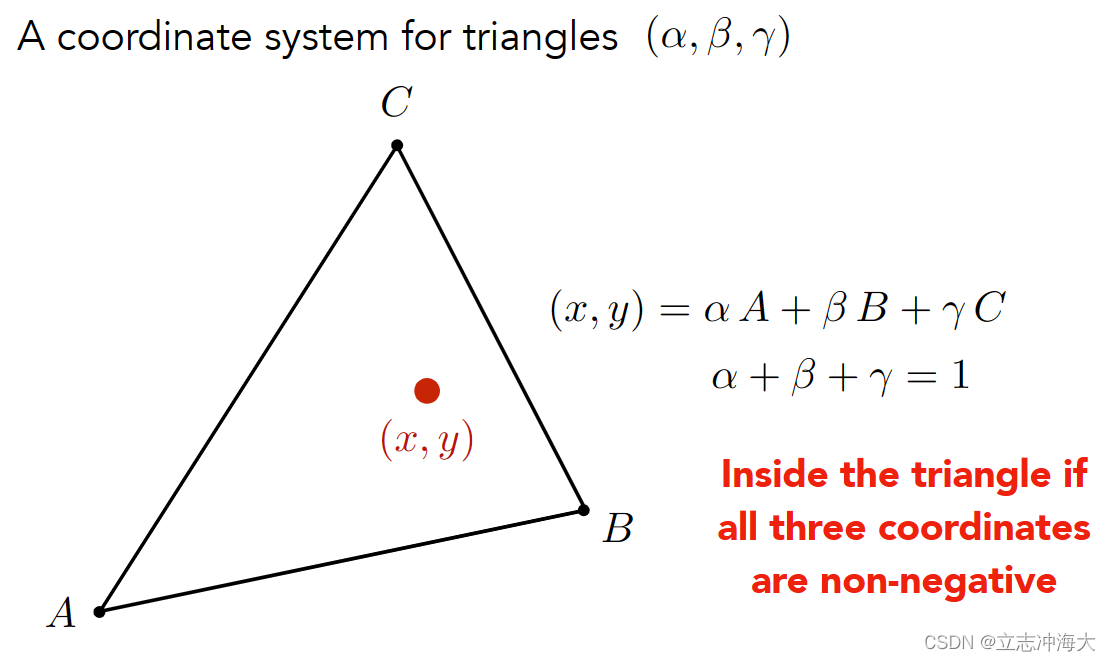
A coordinate system for triangles(α ,β ,γ):重心坐标
三角形所在平面上任意一点xy,都可以用三个顶点他们坐标的线性组合来表示,只要满足一个条件(α +β +γ=1)。等于1是为了现在这个点在三角形所在的平面内
如果这个点在三角形内还需要满足(α ,β ,γ)这三个系数必须是非负的。Inside the triangle if all three coordinates are non-negative
1.A点自己的重心坐标
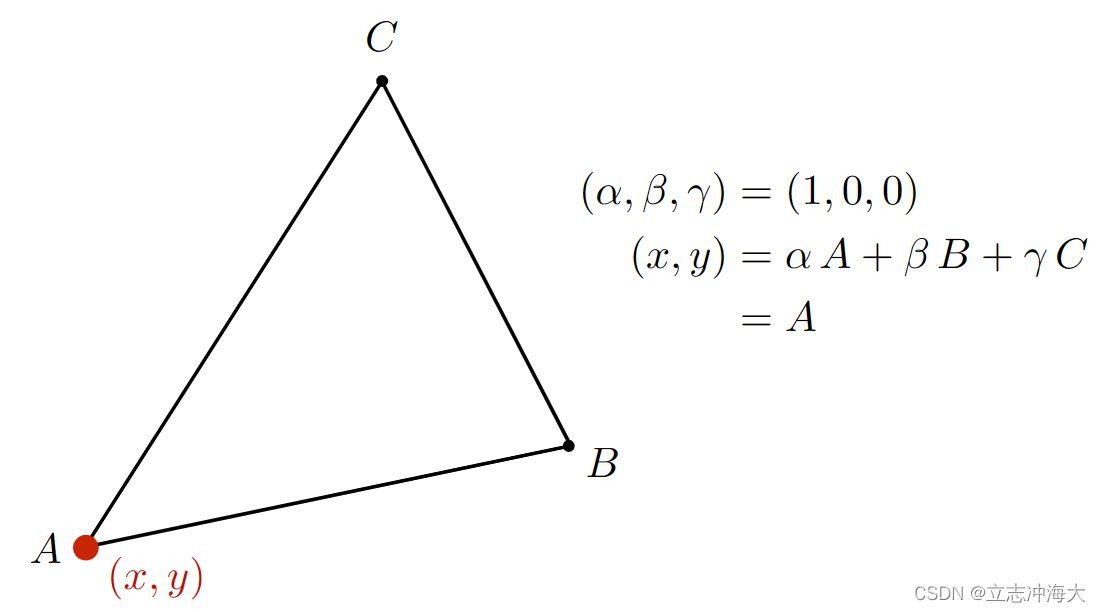
2.如何求出任意点的重心坐标?
——利用小三角形的面积求
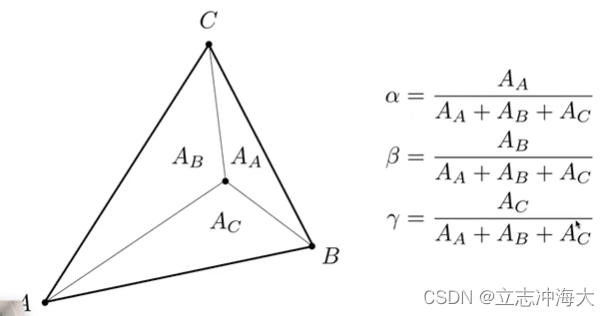
三角形自己的重心坐标:(1/3,1/3,1/3),把三角形分为了3个等面积的三角形
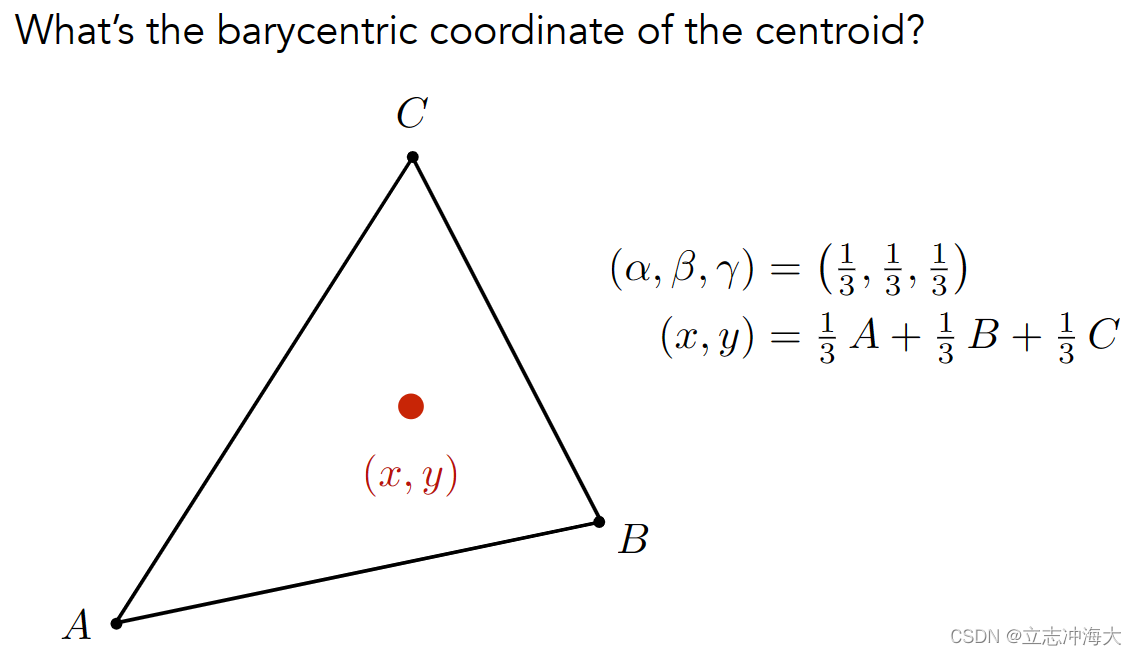
投影后重心坐标会发生变化,那么如何把已经投影到屏幕上的坐标再投影回去呢?使用逆变换
也就是说在三维空间中的属性建议在三维空间中做差值然后再把这个值对应到二维结果上去
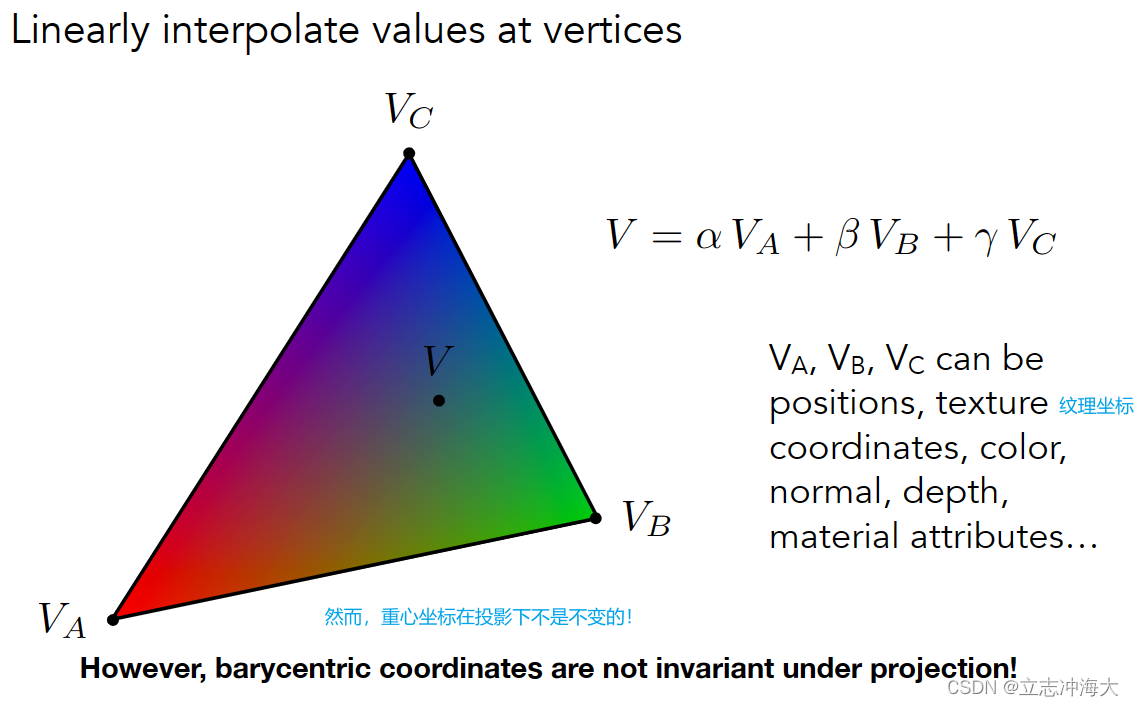
任何一个点只要有重心坐标就可以差值任何的属性。
2.如何把纹理应用在实际的渲染中?Applying Textures
屏幕上任何一个采样点都有一个位置,都对应一个纹理坐标uv,之前纹理坐标都定义在三角形的顶点上,现在都可以算出来了。
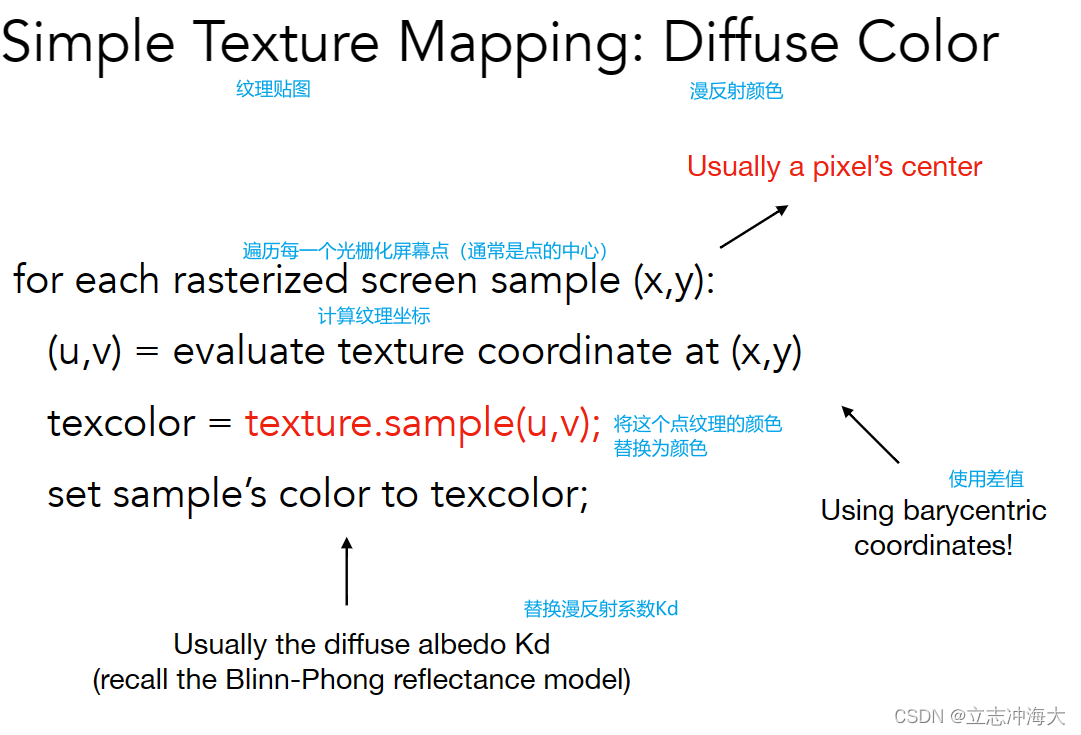
那么如果这样做会出现什么问题呢?
3.Texture Magnification纹理放大。(解决纹理小的问题)
如果纹理太小怎么办(如果纹理只有256*256但要求分辨率为4k的墙进行渲染),也就是说我们看一个很高分辨率的墙,任意一个点去查这个纹理的时候,会查到一些非整数的值,也就是说纹理太小了,纹理就会被拉大。
解决办法:
对于任何墙上的一个点(一个像素),都可以找到它对应的纹理上的一个位置,这个位置可能不是整数,那我们就把它四舍五入为整数。
但是这样也会产生不好的视觉效果,因为一小块点的像素都被划分为了同样的颜色纹理,没有平滑的过渡。

双线性差值Bilinear Interpolation:做了两趟差值,水平一趟竖直一趟。
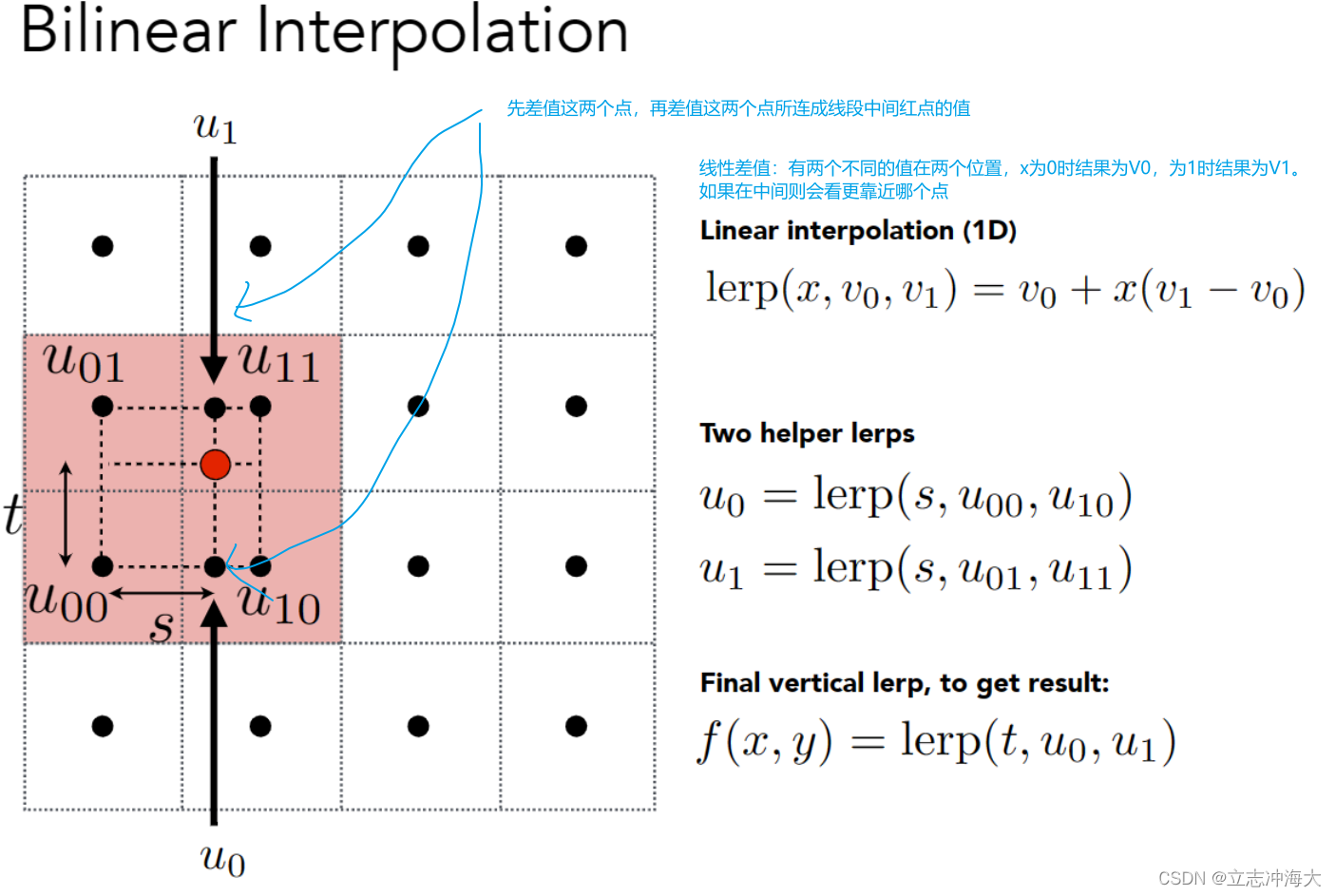
这样的话小红点就综合考虑了它周边4个点的颜色,目的是达到平滑过渡。

Bicubic:取临近16个做水平和竖直的差值,每次用4个做三次的差值,运算量大效果好。
4.Texture Magnification (hard case) 如果纹理太大怎么办?
近处会产生锯齿,远处会产生摩尔纹
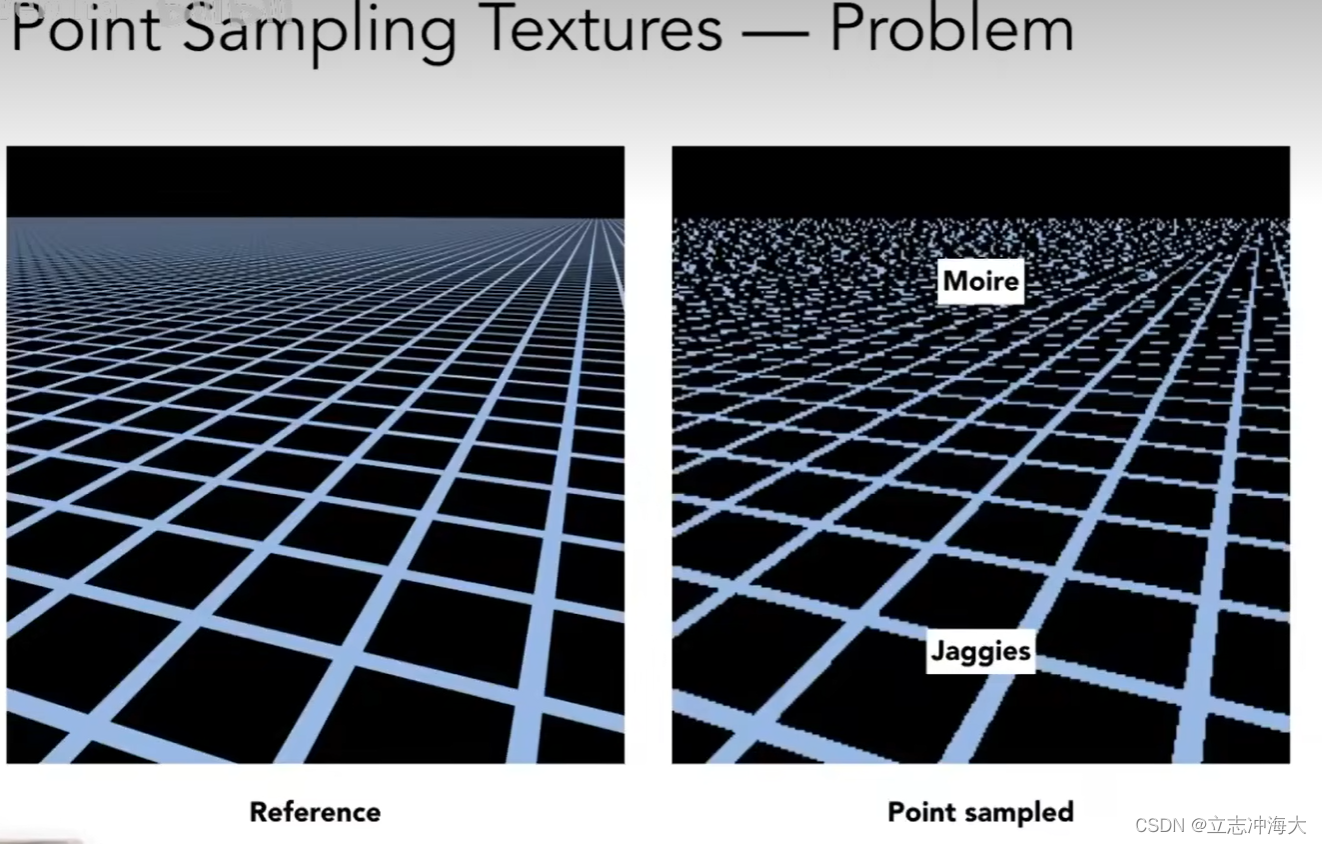
当像素覆盖的纹理区域比较大的时候,不能简单的用中心点的特征来评判整个像素的特征这样简单的采样。
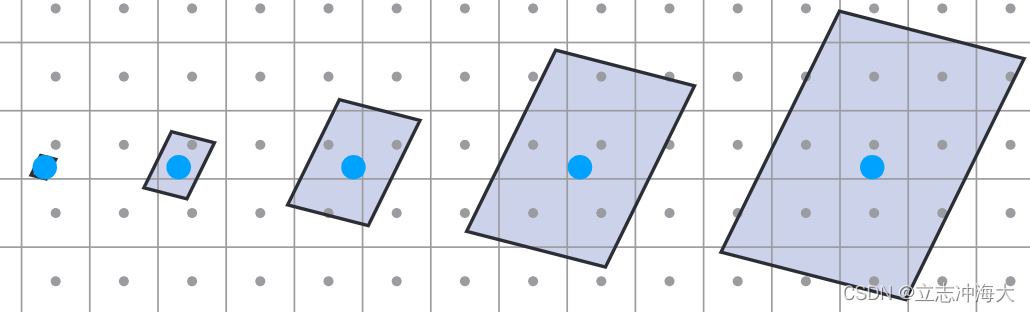
如果使用超采样(一个像素用更多的样本来采样,比如右图512个点取平均)来解决,可以得到很好的结果但运算量会很大。

复习:走样是怎么来的?
答:采样的速度跟不上信号的频率,也就是信号变化过快。
当纹理特别大时,一个像素的像素内部就会包含很大一块纹理,这块纹理一直在变化,也就是说在一个像素内它的频率很高,可我们只用了一个采样点去采样。
一个像素内它有着非常高频的信息,我们希望把这个像素内的值给重构出来,那我们就应该需要一个更高频的采样方法,这就是为什么我们需要非常多采样点的原因。、
我们不想用这么多的采样点怎么办?既然采样会引起走样那我们不采样不就行了!
避免采样:像素会在纹理上覆盖很大一块区域,如果我立刻可以知道这块区域它的值平均是多少。
补充知识:点查询和范围查询。点查询:例如双线性差值,范围查询:例如找范围内的平均值
Mipmap范围查询
Allowing (fast, approx., square) range queries 允许快,近视,方形
逐步把一个图的分辨率缩小一半

每次存储量是原本的1/4,因为每次边长都砍去了一半,有四条边。也就是所有的图加起来最终比原来多出1/3的存储量。
Trilinear Interpolation三线性差值
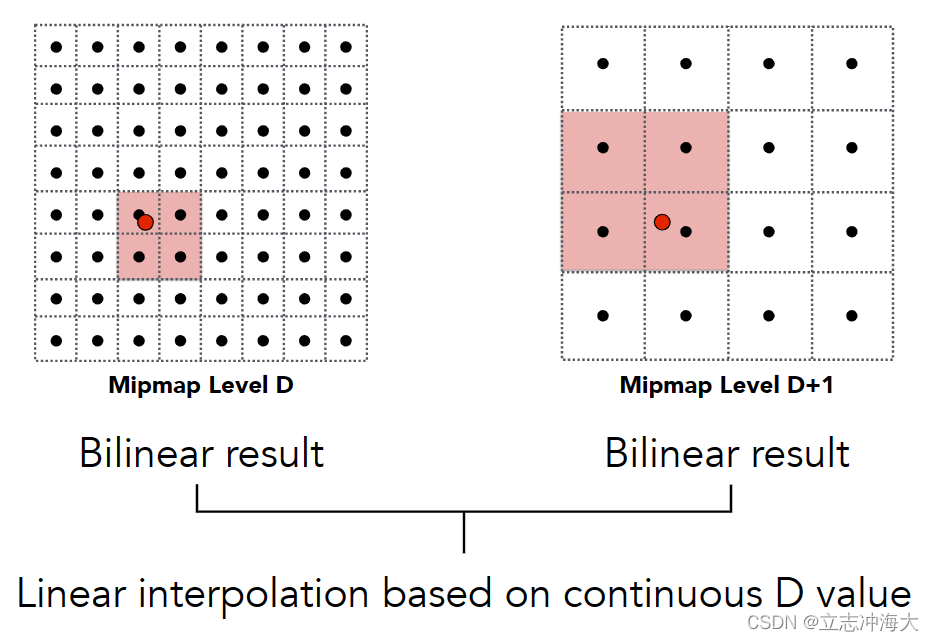
将两个相邻层的双线性差值结果再差值一次就可得到三线性差值,例如求1.8层的话最初就是1层和2层的双线性差值结果

从三线性差值的结果可以看出,不同层次之间都有颜色渐变的过渡。
但是mipmap也会产生一些问题,比如会把远处的图像Overblur模糊过分了。

这是因为mipmap只能查询正方形区域内范围查询它的平均值,其差值也是近似出来的。
各向异性(在不同的方向上表现各不相同)过滤
允许对长方形的区域做快速范围查询。总共开销是原本的3倍