一、题目

路径被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中至多出现一次。该路径至少包含一个节点，且不一定经过根节点。

路径和是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其最大路径和。

示例 1：

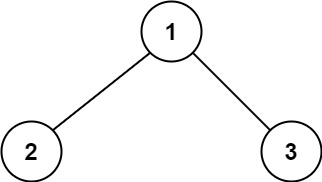
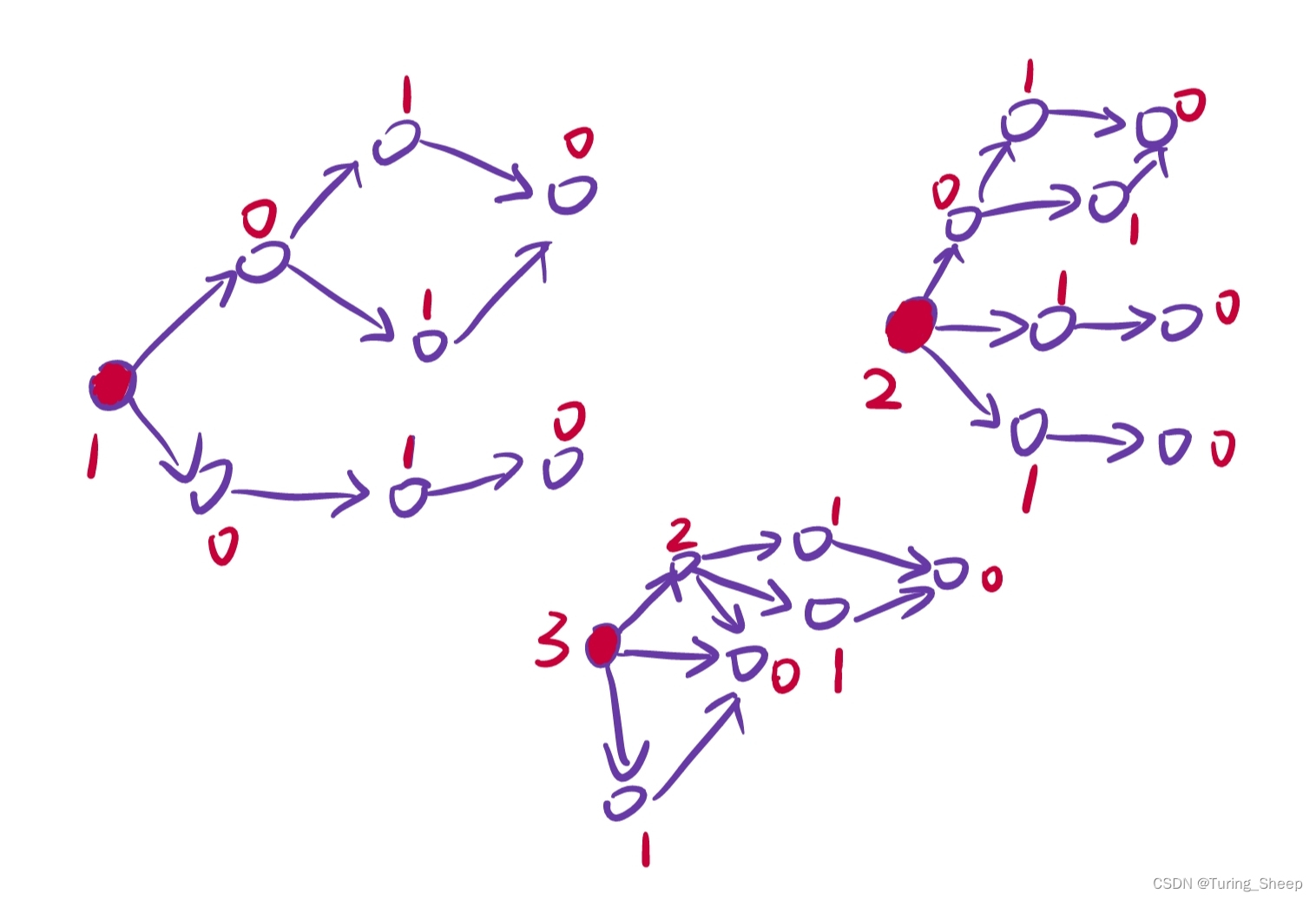
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

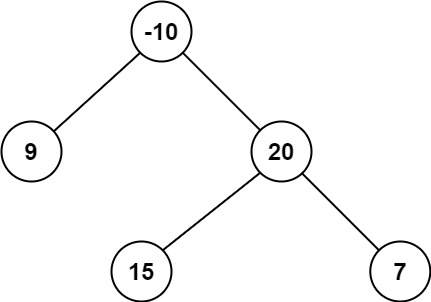
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

树中节点数目范围是 [1, 3 * 104]
-1000 <= Node.val <= 1000

二、代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public class Info{
        // 从左子树或者右子树延伸出来的连到x节点的最大路径和（注意这个只是从左子树或右子树开始连到x为止的路径，并不是从左子树跨过x再连到右子树的路径）
        public int maxPathSumFromHead;
        // 以当前节点为根节点的整棵树的最大路径和（路径并不一定要过x节点）
        public int maxPathSum;

        public Info(int maxPathSumFromHead, int maxPathSum) {
            this.maxPathSumFromHead = maxPathSumFromHead;
            this.maxPathSum = maxPathSum;
        }
    }

    public int maxPathSum(TreeNode root) {
        // 无效参数
        if (root == null) {
            return 0;
        }

        // 返回root的maxPathSum信息
        return process(root).maxPathSum;
    }

    // 二叉树递归
    public Info process(TreeNode x) {
        // basecase  空的话直接返回null，让上层去做相关的判断
        if (x == null) {
            return null;
        }

        // 通过递归获得左右子树的信息
        Info leftInfo = process(x.left);
        Info rightInfo = process(x.right);

        // 1、先计算maxPathSumFromHead。一共就有三种情况：1)只有x 2）x往左扎 3）x往右扎
        // 先将maxPathSumFromHead初始化为x.val，情况一
        int maxPathSumFromHead = x.val;
        // 每一步操作都要先判断leftInfo和rightInfo是否为空
        // 去比较x往左扎的路径最大值是否是比maxPathSumFromHead大，大则更新maxPathSumFromHead，情况二
        if (leftInfo != null) {
            maxPathSumFromHead = Math.max(maxPathSumFromHead, x.val + leftInfo.maxPathSumFromHead);
        }
        // 去比较x往右扎的路径最大值是否是比maxPathSumFromHead大，大则更新maxPathSumFromHead，情况三
        if (rightInfo != null) {
            maxPathSumFromHead = Math.max(maxPathSumFromHead, x.val + rightInfo.maxPathSumFromHead);
        }

        // 2、再计算以x为根节点的整棵树的最大路径和maxPathSum。
        // 一共就有六种情况：1) 只有x  2)左树整体的最大路径和（不过x节点，也就是左树的maxPathSum） 3) 右树整体的最大路径和（不过x节点，也就是右树的maxPathSum）  4)从左树连接到x节点的最大路径和（只有x到左树的路径）   5)从右树连接到x节点的最大路径和（只有x到右树的路径）  6)从左树连接到x节点，再延伸到右树的最大路径和
        // 先将maxPathSum初始化为x.val，情况一
        int maxPathSum = x.val;
        // 去比较左子树的最大路径和是否是比maxPathSum大，大则更新maxPathSum，情况二
        if (leftInfo != null) {
            maxPathSum = Math.max(maxPathSum, leftInfo.maxPathSum);
        }
        // 去比较右子树的最大路径和是否是比maxPathSum大，大则更新maxPathSum，情况三
        if (rightInfo != null) {
            maxPathSum = Math.max(maxPathSum, rightInfo.maxPathSum);
        }

        // 去比较左子树连接到x的最大路径和是否是比maxPathSum大，大则更新maxPathSum，情况四
        if (leftInfo != null) {
            // 这个是利用x.val + leftInfo.maxPathSumFromHead求出来的
            maxPathSum = Math.max(maxPathSum, x.val + leftInfo.maxPathSumFromHead);
        }
        // 去比较右子树连接到x的最大路径和是否是比maxPathSum大，大则更新maxPathSum，情况五
        if (rightInfo != null) {
            maxPathSum = Math.max(maxPathSum, x.val + rightInfo.maxPathSumFromHead);
        }
        // 去比较左子树连接到x，再跨国x连接到右子树的最大路径和是否是比maxPathSum大，大则更新maxPathSum，情况六
        if (leftInfo != null && rightInfo != null) {
            // 这个是利用x.val + leftInfo.maxPathSumFromHead + rightInfo.maxPathSumFromHead求出来的
            maxPathSum = Math.max(maxPathSum, x.val + leftInfo.maxPathSumFromHead + rightInfo.maxPathSumFromHead);
        }

        // 返回以当前x节点为根节点的树的Info信息
        return new Info(maxPathSumFromHead, maxPathSum);
    }
}