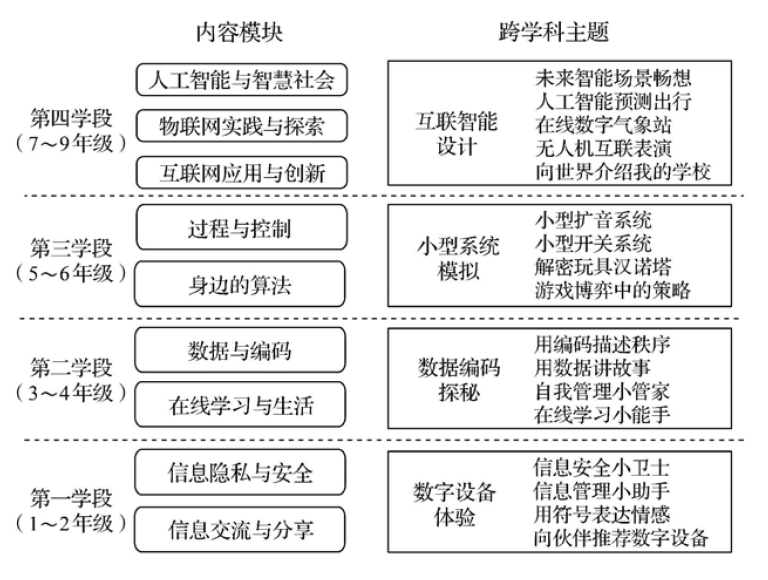
最长公共子序列
- 一、题目
- 二、思路
- 1、状态转移方程
- (1)状态表示
- (2)状态转移
- 2、循环设计
- 三、代码
一、题目

二、思路
这道题是一个很经典的DP问题,那么我们来看一下如何分析。
DP问题我们需要考虑两个问题:第一个问题就是状态转移方程的书写,第二个问题就是我们如何去设计循环。
第一个问题的作用是有效地实现状态之间的转移,第二个问题的作用是保证我们能够从小到大,不重不漏的枚举出每一个子问题。
1、状态转移方程
(1)状态表示
状态的表示一个关键因素就是能够表示这个问题的规模大小。
由于这道题设计到了两个字符串,那么我们利用
f
(
i
,
j
)
f(i,j)
f(i,j)来表示,
f
(
i
,
j
)
f(i,j)
f(i,j)的意思是,从左向右看,以第
i
i
i个字母结尾的字符串1和以第
j
j
j个字母结尾的字符串2之间最长的公共子序列长度。而这个长度要存储在二维数组
f
[
i
]
[
j
]
f[i][j]
f[i][j]中。
(2)状态转移
状态转移的目的是利用子问题间接地去解决问题。
根据我们的状态表示,我们只知道每个字符串的最后一个字符。那么我们就从此入手。
对于最长公共子序列而言,其实无非就4种情况,要么肯定不包含字符串1中的第 i i i个字母,要么肯定不包含字符串2中的第 j j j个字母,要么肯定不包含两个字母,要么肯定都包含。两个都包含的话其实是有前提的,那么就是 s t r 1 [ i ] = s t r 2 [ j ] str1[i]=str2[j] str1[i]=str2[j],如果已经确定了我们要选最后一个字符的话,我们第四种情况就可以写成: f [ i ] − 1 [ j − 1 ] + 1 f[i]-1[j-1]+1 f[i]−1[j−1]+1。
那么我们怎么知道这四种情况哪个是最长的呢?我们只需要比较一下求一下最大值即可。
那么我们此时来考虑一下,这几个情况之间是否有重合的部分呢?其实是有的。
我们以
f
[
i
]
[
j
]
f[i][j]
f[i][j]为例,按照刚刚的思路我们需要比较的是:
f
[
i
−
1
]
[
j
−
1
]
f[i-1][j-1]
f[i−1][j−1],
f
[
i
−
1
]
[
j
]
f[i-1][j]
f[i−1][j],
f
[
i
]
[
j
−
1
]
f[i][j-1]
f[i][j−1],
f
[
i
−
1
]
[
j
−
1
]
+
1
f[i-1][j-1]+1
f[i−1][j−1]+1
我们分类的方式是肯定不包含某个字母,但是另一个字母是可能包含可能不包含,是否包含的情况其实根据两种情况下的公共序列长度而定的,也就是说我们在分析
f
[
i
−
1
]
[
j
]
f[i-1][j]
f[i−1][j],
f
[
i
]
[
j
−
1
]
f[i][j-1]
f[i][j−1]这两种情况的时候,就已经考虑到了
f
[
i
−
1
]
[
j
−
1
]
f[i-1][j-1]
f[i−1][j−1]的情况。
因此我们只需要考虑最后三种情况。
那么我们的状态转移方程可以写成
f ( i , j ) = { m a x ( f ( i , j − 1 ) , f ( i − 1 , j ) ) i ≠ j m a x ( f ( i , j − 1 ) , f ( i − 1 , j ) , f ( i − 1 , j − 1 ) + 1 ) i = j f(i,j)= \begin{cases} max\big(f(i,j-1),f(i-1,j)\big)&i\neq j\\ max\big(f(i,j-1),f(i-1,j),f(i-1,j-1)+1\big)&i=j\\ \end{cases} f(i,j)={max(f(i,j−1),f(i−1,j))max(f(i,j−1),f(i−1,j),f(i−1,j−1)+1)i=ji=j
2、循环设计
我们的外层循环设计为一个字符串长度,第二层循环设计为另一个字符串的长度。这样我们就能逐步地扩大问题规模。
这种循环设计是很常用的。比如背包问题中,我们就经常这样设计。
三、代码
#include<iostream>
using namespace std;
const int N=1e3+10;
int f[N][N];
int n,m;
char s1[N],s2[N];
int main()
{
cin>>n>>m;
scanf("%s%s",s1+1,s2+1);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
f[i][j]=max(f[i][j-1],f[i-1][j]);
if(s1[i]==s2[j])f[i][j]=max(f[i][j],f[i-1][j-1]+1);
}
}
cout<<f[n][m]<<endl;
}