目录
二叉树的性质及其问题:
二叉树的性质
问题:
一、对称的二叉树:
题目:
解题思路:
二、另一棵树:
题目:
解题思路:
三、翻转二叉树:
题目:
解题思路:
四、层序遍历:
概念:
核心代码:
衍生问题:
1、一层一层的打印结点元素
思路分析:
代码分析:
代码演示:
2、判断是否是完全二叉树
思路分析:
代码演示:
队列代码:
头文件:
源文件:

二叉树的性质及其问题:
二叉树的性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有 个结点.
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是 .
3. 对任何一棵二叉树, 度为0的结点 始终 比 度为 2 的结点个数多1 ,当结点个数是奇数时度为1的结点个数是1
4. 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h= log 2 (n+1). (ps: 是 log以2 为底,n+1为对数),又可以将高度 h 和 结点个数 换算为公式 [2^(h-1),2^h -1 ] 结点个数就在这个区间至内。
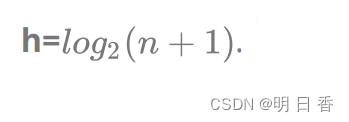
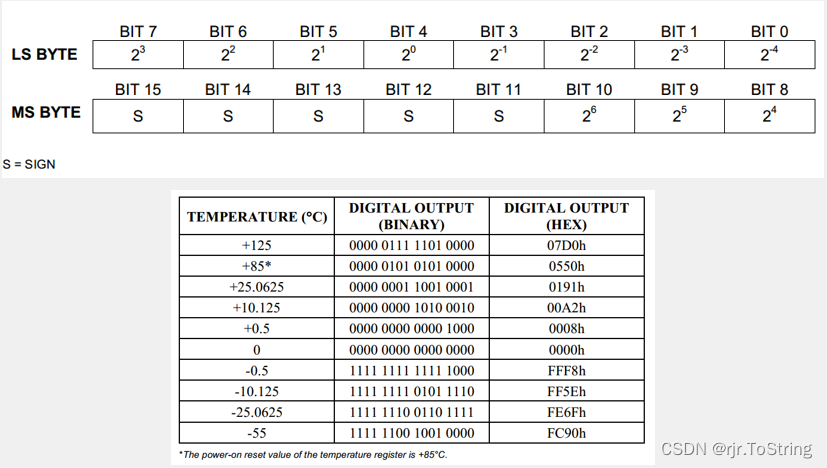
5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对 于序号为i的结点有:
- 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
- 若2i+1>=n 否则无左孩子
- 若2i+2>=n 否则无右孩子
问题:
1、在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
解答:
2、一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12
解答:使用[2^(h-1),2^h -1 ] 进行带入判断
3、一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383
B 384
C 385
D 386
解答:
一、对称的二叉树:
题目:
给你一个二叉树的根节点
root, 检查它是否轴对称。
题源:101. 对称二叉树 - 力扣(LeetCode)
解题思路:
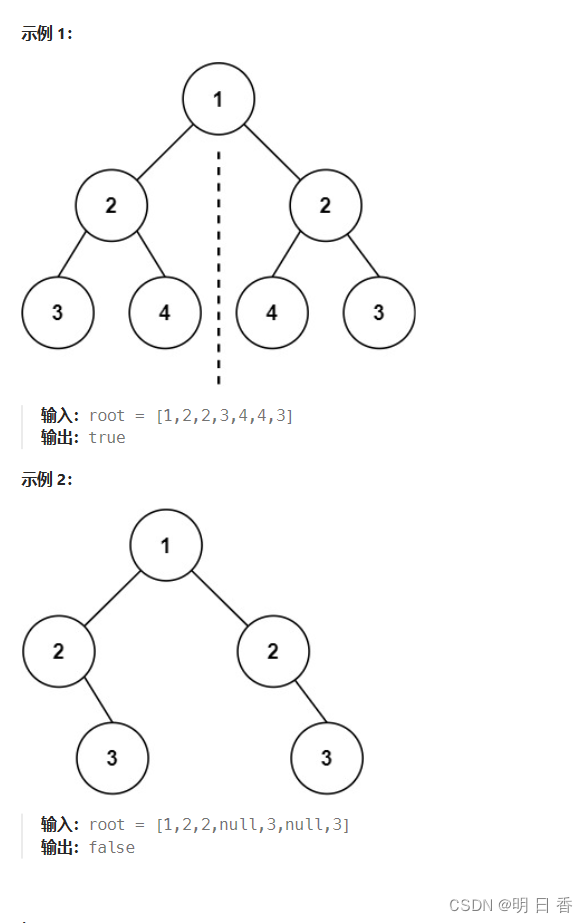
按照图例来看,若想判断一个二叉树是否是图中的样子,那么需要将将二叉树分为两个部分,也就说将一棵二叉树当成两个部分,除去根结点,对左右子树部分进行相对应的比较。
也就说将左子树部分的左孩子和右子树部分的右孩子进行比较和左子树的右孩子和右子树的左孩子进行比较,将比较分为两个部分进行。
- 所以本题是将二叉树分为两个子树,而又将两颗子树的左右孩子进行分开配对比较。


二、另一棵树:
题目:
- 给你两棵二叉树
root和subRoot。检验root中是否包含和subRoot具有相同结构和节点值的子树。如果存在,返回true;否则,返回false。- 二叉树
tree的一棵子树包括tree的某个节点和这个节点的所有后代节点。tree也可以看做它自身的一棵子树。
题源:572. 另一棵树的子树 - 力扣(LeetCode)

解题思路:
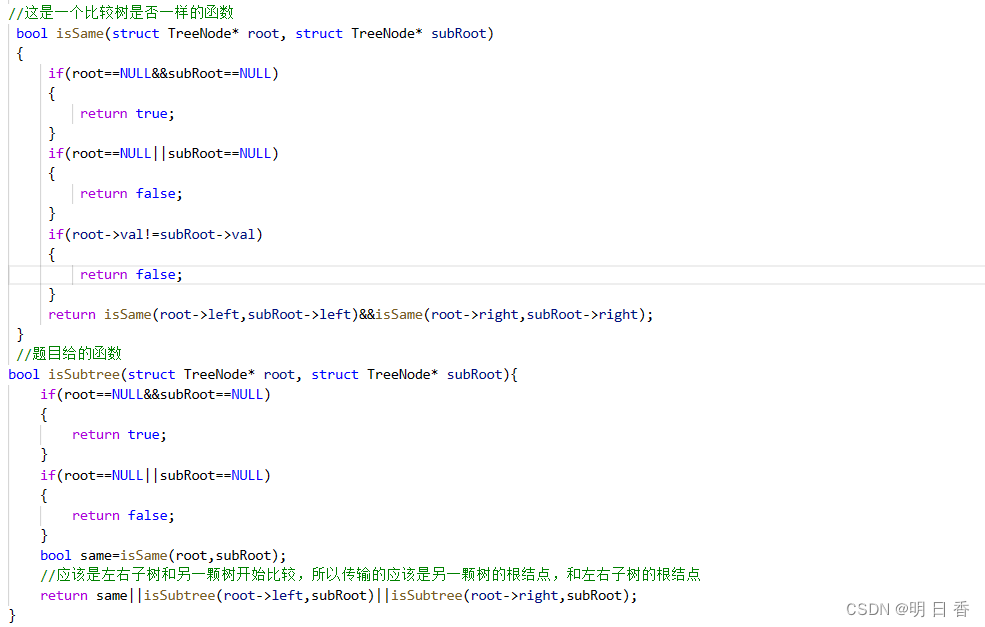
如图所示,我们需要检查一颗大树内部是否有着小树的存在,即大树的内部是否包含了小数,与之前的<查找两棵树是否相同:100. 相同的树 - 力扣(LeetCode)>类似。
也需要用到这一题的代码进行查询,而在查询之前,我们首先将本题的查找分为三个部分,第一,从根结点开始找,第二从左子树开始找,第三从右子树开始找。
从三个方面开始寻找,寻找的过程中可以很显然意见的发现,问题被化解为了以查询是否和小树同时存在该结点,如果同时存在结点的数值是否和小树的一样。
- 如果都一样,那么再度开始进行调用遍历,查询下一个结点是否一致。

三、翻转二叉树:
题目:
给你一棵二叉树的根节点
root,翻转这棵二叉树,并返回其根节点。
题源:226. 翻转二叉树 - 力扣(LeetCode)

解题思路:
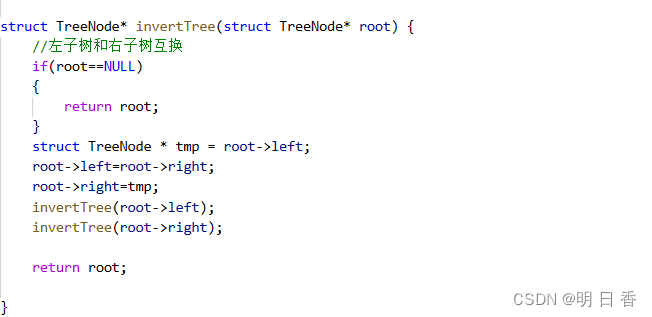
- 如图例所示,翻转二叉树是将左右子树进行交换,且并不是单纯的一次交换,而是以每个结点为根结点,其下的左右孩子结点进行了交换。
所以,面对这种问题可以采取一个非常简单的思路,交换地址,因为我们当前的二叉树结构是链式二叉树,所以在链式二叉树中的左右孩子结点的指针是地址,所以只要把左右孩子结点的指针内部的地址进行交换即可。
四、层序遍历:
概念:
层序遍历是二叉树遍历的一种,且是在二叉树的四种遍历中较为复杂的一种,因为层序遍历需要使用到队列。
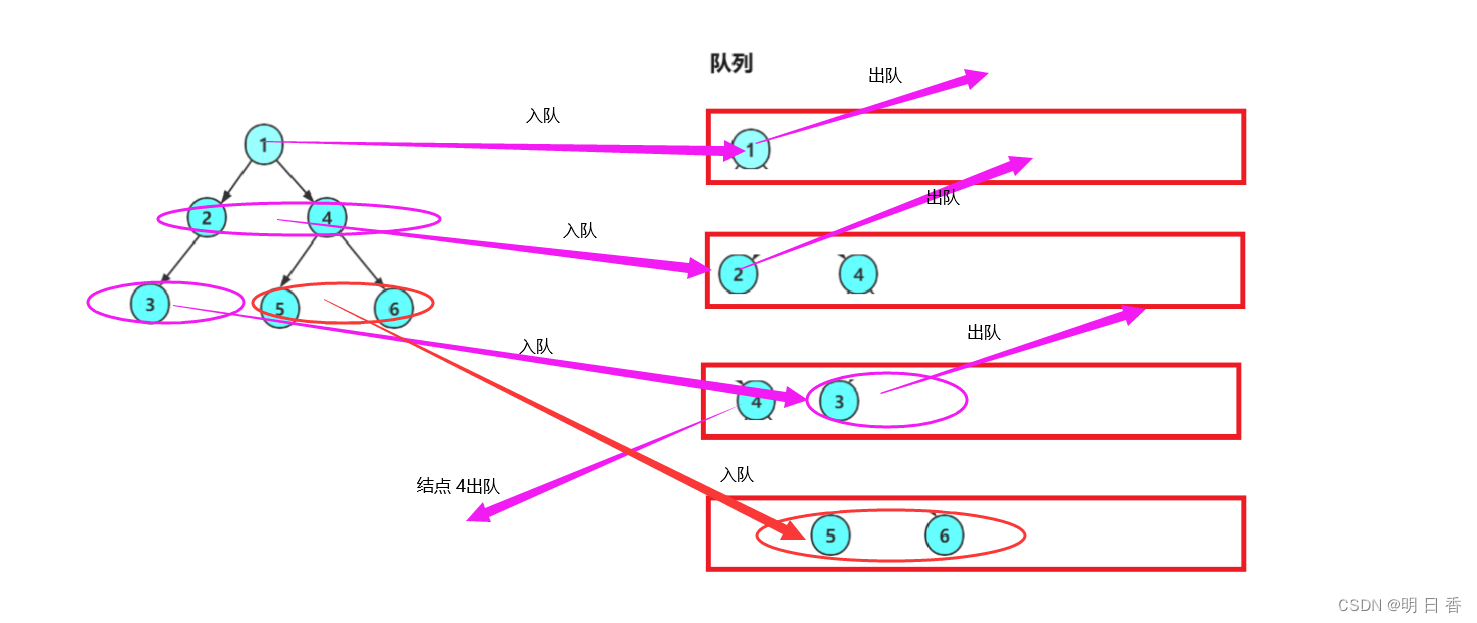
如图所示,层序遍历便是将二叉树中的每一层的结点放入队列中,以入队的形式存放到队列中,而当每一个结点进入后,又会马上的出队,且出 队后会将该结点的左右孩子结点送入队列中,等到队列完全为空时,层序遍历才遍历完成。
而在层序遍历中,我们需要用到的队列函数有:入队、出队、判断队列是否为空、获取队头元素,其中,判断队列是否为空是判断层序遍历是否结束的语句,获取队头元素是为了方便出队,入队则是要结点的左右孩子结点进入队内。
核心代码:

代码分析

衍生问题:
1、一层一层的打印结点元素


思路分析:
如上图所示,要求我们将结点的元素如图所示进行打印,而这种打印也就是将每一层都使用 \n 进行隔离,而需要使用 \n 进行隔离,可以转化为,如何将每一层完美的分离。
- 这里就需要用到队列的一个特点,先进先出,因为每一次出去的结点都会将它的左右孩子结点带入队列中,所以可以计算孩子结点的个数作为循环判断。

代码分析:
假设当前这一层的结点个数是N,那么在出队的同时会带入孩子结点,当这一层的结点全部出队,而在对内,当前这一层的结点个数是0,而孩子结点则是2N(假设每一个结点都有左右孩子结点),然后以结点个数是否是0为判断,跳出了循环,随后打印回车,随后又因为队列不为空而进入层序遍历,同时再次之前进行孩子结点的个数统计,准备进行下一层的循环。
代码演示:

2、判断是否是完全二叉树
完全二叉树概念:树与二叉树堆:二叉树-CSDN博客
思路分析:
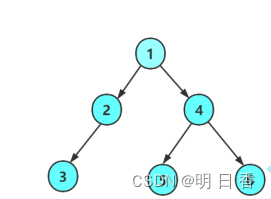
如图所示,如果不是完全二叉树,那么按照层序遍历的思想,那么在层序遍历时必然会有一个结点没有带入它的左右孩子结点,因为它的左右孩子结点不存在或者说是NULL。
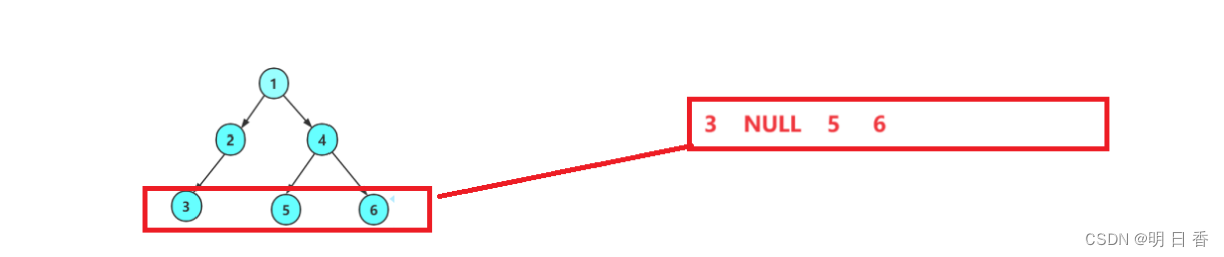
而本题中,我们可以取消对左右孩子结点是否存在的判断,从而当最后出队时,必然会出现值为NULL的结点出队,所以以此来进行判断。
当出现NULL之后,队列内还有元素(结点)存在,那么这颗树便不是完全二叉树。
代码演示:

队列代码:
头文件:

源文件: