emsp;emsp;emsp队栈和Hash的经典问题
用栈实现队列
栈是先进后出,队列是先进先出,所以可以使用两个栈来实现队列的功能。
LeetCode232:
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、
empty):

思路:
(1)一个栈作为输入栈,支持push操作,一个栈作为输出栈,支持pop和peek操作
(2)每次pop或peek时,如果输出栈为空,则把输入栈的元素弹出并压入输出栈,此时输出栈从栈顶到栈尾的顺序就是队列从队首道队尾的顺序
class MyQueue{
Deque<Integer>inStack;
Deque<Integer>outstack;
public MyQueue(){
inStack = new LinkedList<Integer>();
outStack = new LinkedList<Integer>();
}
public void push(int x){
inStack.push(x);
}
public int pop(){
if (outStack.isEmpty()) in2out();
return outstack.pop();
}
public int peek(){
if (outstack.isEmpty()) in2out();
return outstack.peek();
}
public boolean empty(){
return instack.isEmpty() && outstack.isEmpty();
}
private void in2out(){
while (!instack.isEmpty()) outstack.push(instack.pop());
}
}
用队列实现栈
leetcode225:
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop和empty)。
实现MyStack类:

思路:同样,可以使用两个队列来实现栈。为了满足栈道特性,要满足最后入栈道元素位于队列的队首。
那么可以使用queue1用于存储栈内的元素,queue2作为入栈操作的辅助队列。
入栈时,将将元素入队到queue2,然后将queue1的全部元素依次出队后入队到queue2。此时,queue2的前面的元素就是新入栈的元素,再将queue1与queue2互换,则queue1元素即为栈内元素,队头为栈顶
出栈或取栈顶时,取queue1的队头即可
判空时,判断queue1即可
class Mystack{
Queue<Integer>queuel;
Queue<Integer>queue2;
public MyStack(){
queue1 = new LinkedList<Integer>();
queue2 = new LinkedList<Integer>();
}
public void push(int x){
queue2.offer(x);
while (!queue1.isEmpty()) queue2.offer(queue1.poll());
Queue<Integer>temp queue1;
queue1 queue2;
queue2 temp;
}
public int pop(){
return queue1.poll();
}
public int top(){
return queue1.peek();
}
public boolean empty(){
return queue1.isEmpty();
}
}
n数之和专题
我的LeetCode的第一题就是求两数之和的问题,当时还只会暴力,不会Hash之类的方法,看到题解差点劝退了。
事实上除此之外,还有几个类似的问题,例如LeetCode15三数之和,LeetCode18.四数相加和LeetCode454.四数相加ll等等。我们就集中看一下。
3.1 两数之和
LeetCode1.给定一个整数数组nums和一个整数目标值target,请你在该
数组中找出和为目标值target的那两个整数,并返回它们的数组下标。你
可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里
不能重复出现。你可以按任意顺序返回答案。

这种题用两层for循环时间复杂度太高,不采用
可以利用哈希表,把遍历过的值保存起来,这样只需寻找target-nums[i]在哈希表中是否存在即可
class Solution {
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> map = new HashMap<>(); //创建一个哈希表map
for (int i = 0; i < nums.length; i++) { //从数组第一个数遍历到最后一个数
if (map.containsKey(target - nums[i])) return new int[]{map.get(target - nums[i]), i}; //判断 目标值减去当前值 得到的值在哈希表是否存在(一石二鸟,通过一个数找到另一个数),若存在,证明已达到题目的要求,直接返回这两个数的索引位
else map.put(nums[i], i);// 上面的if不成立,把当前值存入map哈希表中,注意,key保存当前整数值,value保存对应的索引值
}
return new int[]{}; //虽然题目保证能找到,但按照语法要求,还是要返回一个int型数组,比如会报错
}
}
3.2 三数之和
如果将两个数换成三个会怎样呢?
LeetCode15.给你一个包含n个整数的数组nums,判断nums中是否存在三个元素a,b,c,使得a+b+c=0?请你找出所有和为0且不重复的三元组。注意:答案中不可以包含重复的三元组。
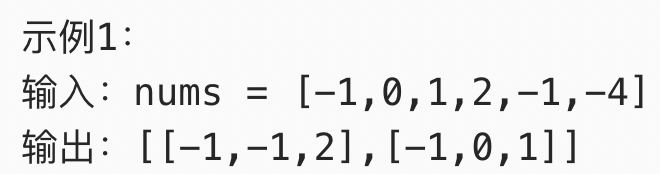
本题看似就是两数增加了一个数,但是难度增加了很多,我们可以使用三
层循环直接找,时间复杂度为O(3),太高了,放弃。
也可以使用双层循环+Hash来实现,首先按照第一题两数之和的思路,我们可以固定一个数target,再利用两数之和的思想去map中存取或查找(-1)*target-num[j],但是这样的问题是无法消除重复结果,例如如果输入[-1,0,1,2,-1,-4],返回的结果是[-1,1,0],[-1,-1,2],[0,1,-1],[0,-1,1],[1,-1,0],[2,-1,-],如果我们再增加一个去重方法,将直接导致执行超时。
那这时候,我们就要想其他方法了,这个公认最好的方式是”排序+双指针我们可以先将数组排序来处理重复结果,然后还是固定一位元素,由于数组是排好序的,所以我们用双指针来不断寻找即可求解,代码如下:
class Solution{
public List<List<Integer>>threeSum(int[]nums){
int n = nums.length;
Arrays.sort(nums);
List<List<Integer>>ans = new ArrayList();
//枚举a
for (int first = 0;first < n; first++){
//需要和上一次枚举的数不相同
if (first > 0 && nums[first] = nums[first - 1]) continue;
//C对应的指针初始指向数组的最右端
int third = n - 1;
int target = -nums[first];
//枚举b
for (int second = first + 1; second < n; second++){
//需要和上一次枚举的数不相同
if (second > first + 1 && nums[second] == nums[second - 1]) continue;
//需要保证b的指针在c的指针的左侧
while (second < third && nums[second] + nums[third] > target) --third;
//如果指针重合,随着b后续的增加
//就不会有满足a+b+c=0并且b<c的c了,可以退出循环
if (second == third) break;
if (nums[second] + nums[third] == target){
List<Integer>list new ArrayList<Integer>();
list.add(nums [first]);
list.add(nums [second]);
list.add(nums [third]);
ans.add(list);
}
}
}
return ans;
}
}