引言

说起排序算法，那可就多了去，首先了解什么叫排序
以B站为例：

蔡徐坤在B站很受欢迎呀，先来看一下综合排序 就是播放量和弹幕量，收藏量 一键三连 都很高这是通过一些排序算法 才能体现出综合排序

蔡徐坤鬼畜 按照播放量来看最高的进行排序，当然也可以按照搜索的结果来进行排序
关键字对于搜索的结果而言非常重要 提供关键字找到对应的视频 在根据关键字对应的视频排序

可能关键字的不同对应的是不同的视频 搜索，排序是算法必备的
同时，还可以考虑用户的个性化推荐，根据用户的观看历史、搜索历史、点赞评论等行为数据，利用机器学习算法进行推荐。这样可以更精准地推荐用户感兴趣的蔡徐坤鬼畜视频，并提高用户的满意度和留存率。

所以排序有非常多种，此时想必疑惑，“这和选择排序有什么关系呢？” 当然有关系。
选择排序是一种简单的排序算法，可以应用到蔡徐坤鬼畜视频排序中。例如，可以根据视频的播放量或者点赞数进行选择排序，按照从大到小的顺序排列视频，从而让用户更容易找到热门的、受欢迎的蔡徐坤鬼畜视频。当然，选择排序只是一种基础的排序算法，对于更复杂的排序任务，需要使用更加高效的排序算法，以提高排序的速度和效率。

选择排序思路

一共是7个数据元素，
只要排序 外层 循环 i=（ 0~ n-1 ） (n>0) 定义maxindex 最大索引默认为0 内层循环j 1到 n-i 比较次数
n-i ：当前还有多少未排序的元素
n-i-1：当前已排序序列的最后一个元素的索引

第一次外层循环
i=0
max=0
第一次内层循环
j=1 j<7-i;
如果 115> 165
j++
直到 j=5 更新maxindex=j
max此时=5
内层 循环遍历结束
如果 这个找到的max的值不等于 当前末尾的值 也就是 n-i-1； 交换数组对应的位置 交换后
第一次外层循环结束

外层循环开始。i代表当前已排序序列的长度（因为每次排序后，i会+1）。外层循环从0开始，到size - 2结束，共进行size - 1次循环。
初始化最大值的索引为0，因为假设第一个元素是当前未排序元素中的最大值。
内层循环开始。j代表当前未排序序列的长度。内层循环从0开始，到size - i - 1结束，每次循环中都寻找未排序序列中的最大值。
如果当前元素大于当前认为的最大值，那么更新最大值的索引。
内层循环结束后，我们得到了未排序元素中的最大值的位置。
如果最大值的索引不等于（size - i - 1），说明最大值不在正确的位置上，需要交换。
交换最大值和最后一个已排序元素的位置。
重复上述步骤，直到所有元素都已排序。

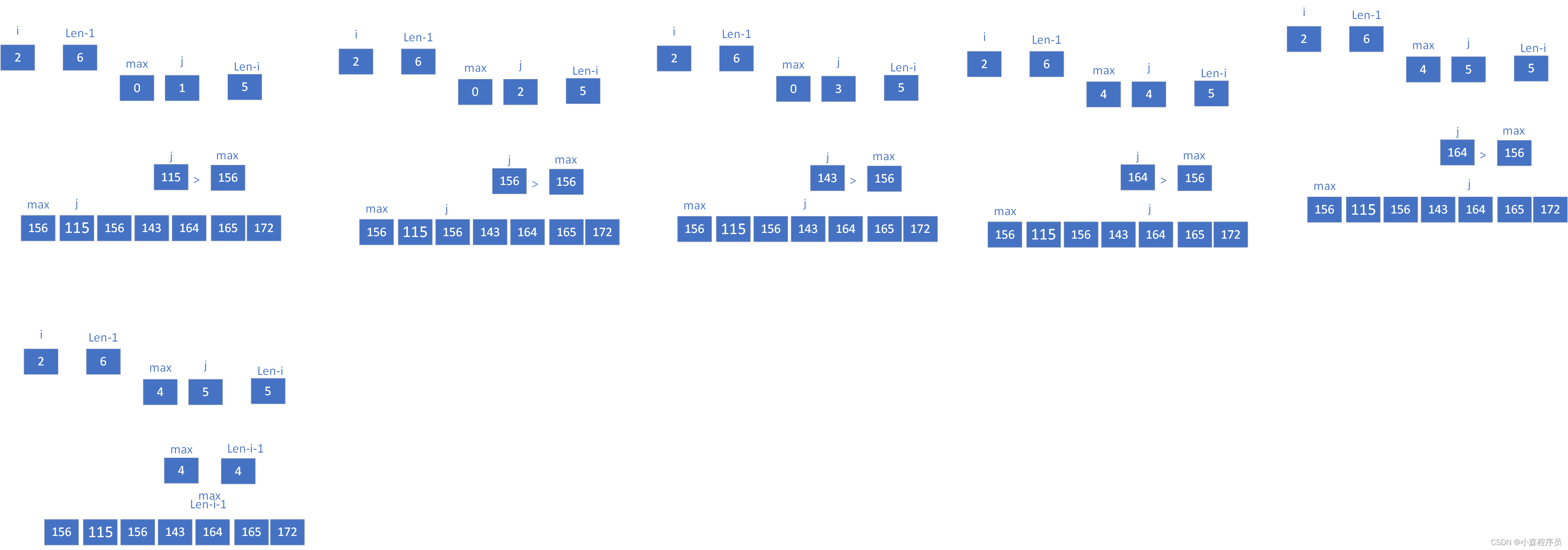
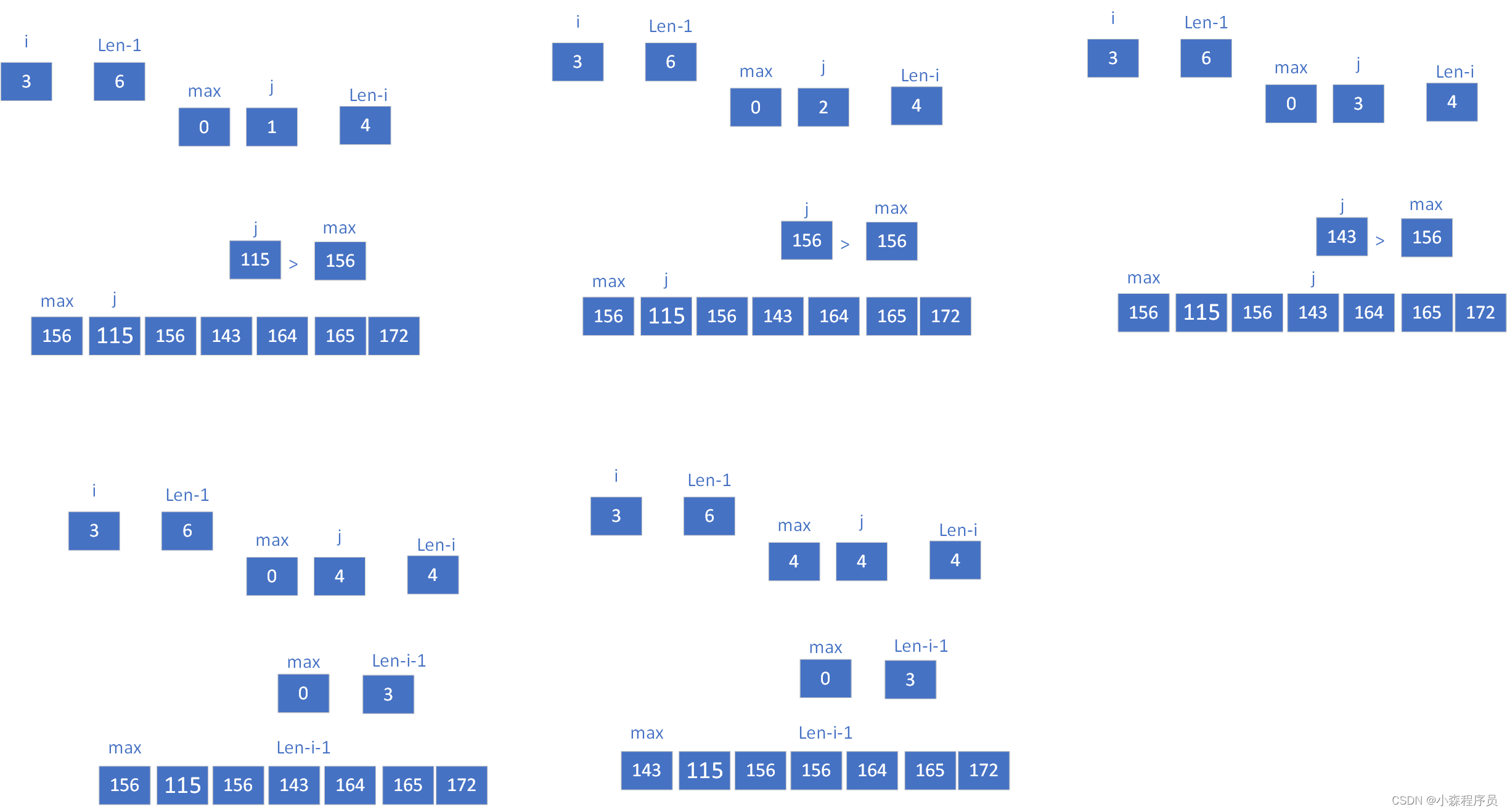
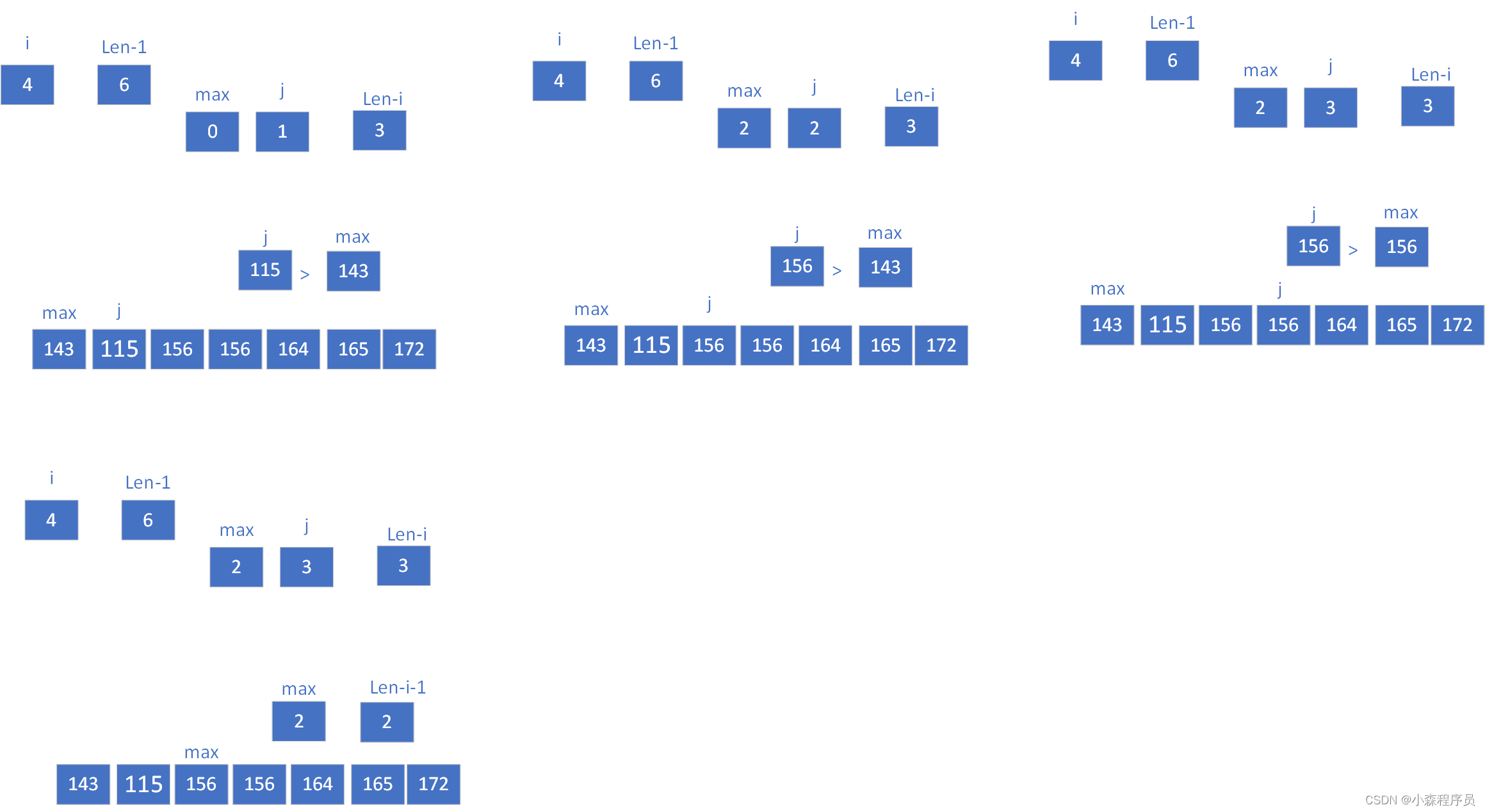
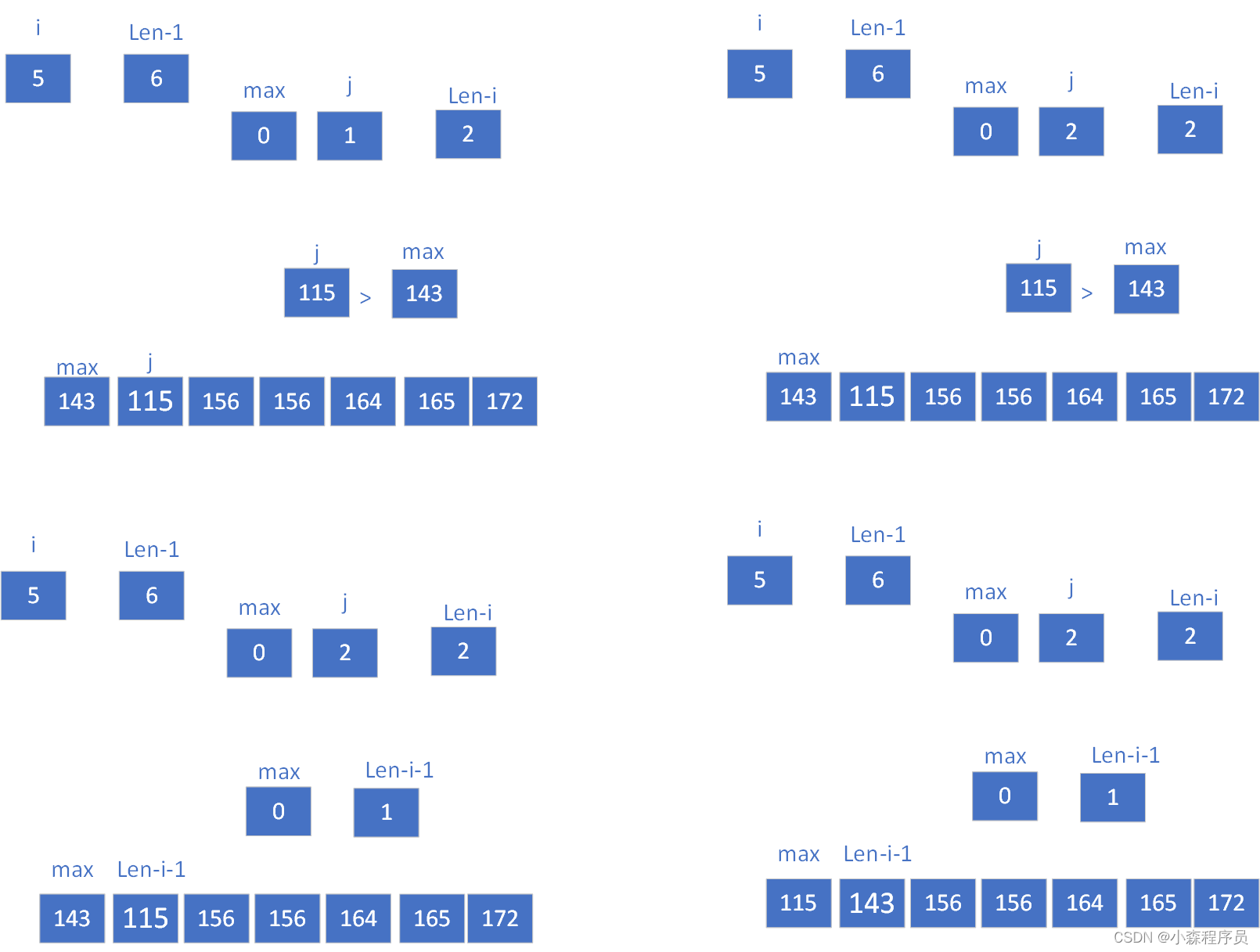
这是每次排序的结果

选择排序算法专区

void SelectSort(int arr[], int size){

// 外层循环开始。i代表当前已排序序列的长度（因为每次排序后，i会+1）  
for (int i = 0; i < size-1; i++) {  
  
    // 初始化最大值的索引为0，因为假设第一个元素是当前未排序元素中的最大值  
    int max = 0;    
      
    // 内层循环开始。j代表当前未排序序列的长度  
    for (int j = 1; j < size - i; j++) {  
          
        // 如果当前元素大于当前认为的最大值，那么更新最大值的索引  
        if (arr[j] > arr[max]) {  
            max = j;  
        }  
    }  
      
    // 如果最大值的索引不等于（size - i - 1），说明最大值不在正确的位置上，需要交换  
    if (max != size - i - 1) {  
        swap(arr[max], arr[size - i - 1]);  // 交换最大值和最后一个已排序元素的位置  
    }  
}

}