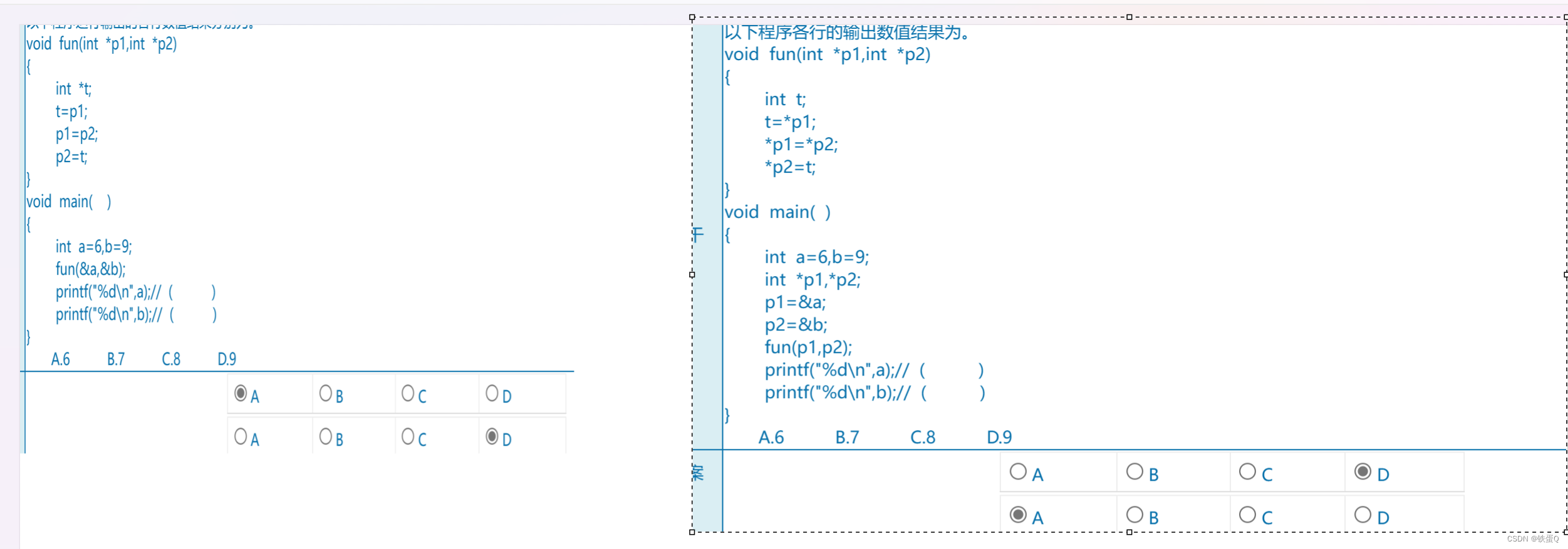
第一题： 寻找满足特定条件的 e；
第一步：

第二步：
由式1.7知，给定e,p,q，就可计算出相应的RSA不动点的数目。因此设计算法步骤如下：

1. 枚举找出所有与φ(n)互素的e。
2. 枚举所有满足条件的e，计算RSA不动点的数目。
3. 以RSA不动点的数目为键，累加变量为值，将每次的结果添加到字典中。
4. 最后输出最小值的键对应的累加值。
   代码以及运行结果如下，结果为399788195976：
   

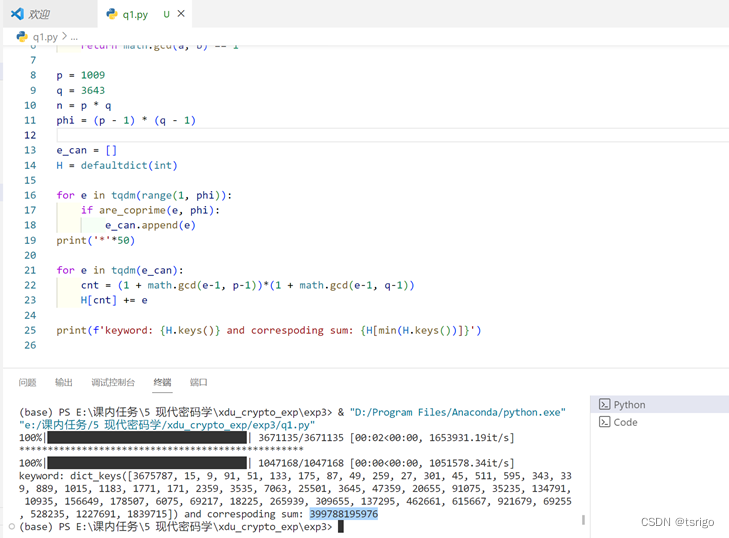
import math
from collections import defaultdict
from tqdm import tqdm

def are_coprime(a, b):
    return math.gcd(a, b) == 1

p = 1009
q = 3643
n = p * q
phi = (p - 1) * (q - 1)

e_can = []
H = defaultdict(int)

for e in tqdm(range(1, phi)):
    if are_coprime(e, phi):
        e_can.append(e)
print('*'*50)

for e in tqdm(e_can):
    cnt = (1 + math.gcd(e-1, p-1))*(1 + math.gcd(e-1, q-1))
    H[cnt] += e

print(f'keyword: {H.keys()} and correspoding sum: {H[min(H.keys())]}')

第二题：
按部就班实现即可，其中求逆元用拓展欧几里得定理。
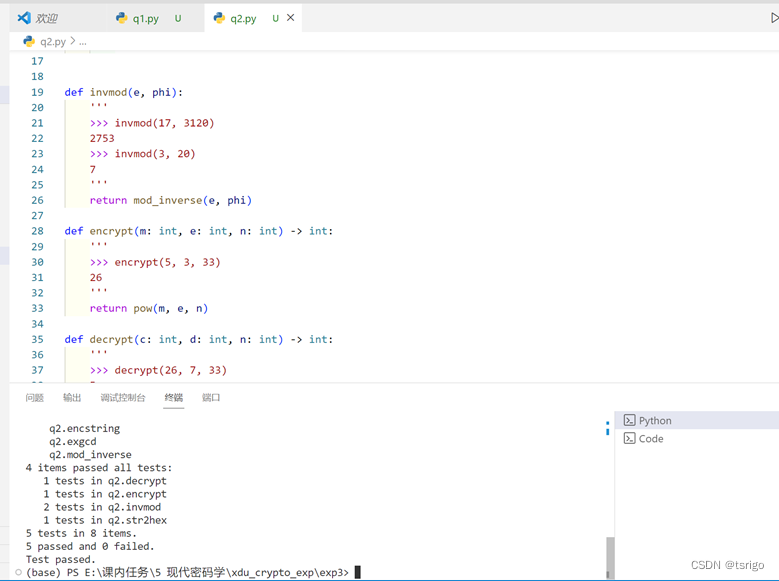
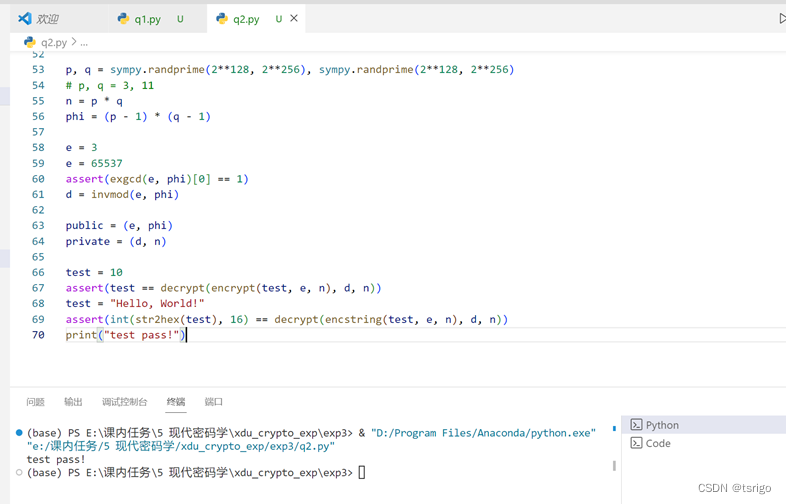
代码和运行结果如下：

import sympy
import binascii

def exgcd(a, b):
    if a == 0:
        return b, 0, 1
    else:
        gcd, x, y = exgcd(b % a, a)
        return gcd, y - (b // a) * x, x

def mod_inverse(a, m):
    gcd, x, _ = exgcd(a, m)
    if gcd != 1:
        raise Exception('Modular inverse does not exist')
    else:
        return x % m


def invmod(e, phi):
    '''
    >>> invmod(17, 3120)
    2753
    >>> invmod(3, 20)
    7
    '''
    return mod_inverse(e, phi)

def encrypt(m: int, e: int, n: int) -> int: 
    '''
    >>> encrypt(5, 3, 33)
    26
    '''
    return pow(m, e, n)

def decrypt(c: int, d: int, n: int) -> int:
    '''
    >>> decrypt(26, 7, 33)
    5
    '''
    return pow(c, d, n)

def str2hex(s):
    '''
    >>> str2hex("Hello, World!")
    '48656c6c6f2c20576f726c6421'
    '''
    return binascii.hexlify(s.encode()).decode()

def encstring(m: str, e: int, n: int) -> int:
    hexstr = str2hex(m)
    return encrypt(int(hexstr, 16), e, n)

p, q = sympy.randprime(2**128, 2**256), sympy.randprime(2**128, 2**256)
# p, q = 3, 11
n = p * q
phi = (p - 1) * (q - 1)

e = 3
e = 65537
assert(exgcd(e, phi)[0] == 1)
d = invmod(e, phi)

public = (e, phi)
private = (d, n)

test = 10
assert(test == decrypt(encrypt(test, e, n), d, n))
test = "Hello, World!"
assert(int(str2hex(test), 16) == decrypt(encstring(test, e, n), d, n))
print("test pass!")