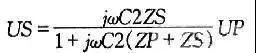1. 极大似然估计与EM算法
极大似然估计是一种常用的参数估计方法,它是以观测值出现的概率最大作为准则。关于极
大似然估计,假设现在已经取到样本值![]() 了,这表明取到这一样本的概率L(θ) 比较
了,这表明取到这一样本的概率L(θ) 比较
大。我们自然不会考虑那些不能使样本![]() 出现的θ作为估计值,再者,如果已知当
出现的θ作为估计值,再者,如果已知当
θ=θ(0)是使L(θ)取很大值,而θ中的其他θ的值使 L(θ)取值很小,自然认为取θ(0)作为未知参数
θ 的估计值较为合理。
在极大似然估计中,独立同分布(IID)的数据![]() , 其概率密度函数为
, 其概率密度函数为![]()
似然函数定义为![]() ,对数似然函数定义为
,对数似然函数定义为![]() ,θ的
,θ的
极大似然估计为![]()
![]() 。
。
极大似然估计存在着问题是:①对于许多具体问题不能构造似然函数解析表达式 ②似然函数
的表达式过于复杂而导致求解方程组非常困难。正是在这种情况下,才提出了EM算法。EM算法主
要用于非完全数据参数估计,它是通过假设隐变量的存在,极大化地简化了似然函数方程,从而解
决了方程求解问题。
计算极大似然估计(maximum likelihood estimate,MLE),需要求似然函数的极值。如求正态
分布均值和方差的MLE:![]()
![]()

观测数据:观测到的随机变量Y的IID样本![]()
缺失数据:未观测到的随机变量Z的值![]()
完整数据:包含观测到的随机变量Y和未观测到的随机变量Z的数据,![]()
![]()
EM算法是一种迭代算法,1977年由Dempster等人总结提出,用于含有隐变量的概率模型参
数的极大似然估计,或极大后验概率估计。EM算法的每次迭代由两步组成:E步,求期望
(Expectation);M步,求极大(Maximization)。所以这一算法称为期望极大算法。
2. 3硬币模型
假设有3枚硬币,分别记作A、B、C。这些硬币正面出现的概率概率分别是a、b、c。进行如
下掷硬币试验:先掷A,根据其结果选出硬币B或C,正面选择硬币B,反面选硬币C;然后掷选出
的硬币,掷硬币的结果,出现正面记作1,出现反面记作0;独立地重复n次试验(这里n=10),观测结
果如下:1、1、0、1、0、0、1、0、1、1
假设只能观测到掷硬币的结果,不能观测到掷硬币的过程。问如何估计三硬币正面出现的概率,即
三硬币模型的参数。三硬币模型可以写作:

这里,随机变量y是观测变量,表示一次试验观测的结果是1或0;随机变量z是隐变量,表示未观测
到的掷硬币A的结果,θ=(a,b,c)是模型参数。注意,随机变量y的数据可以观测,随机变量z的数据
不可观测。
将观测数据表示为![]() ,未观测数据表示
,未观测数据表示![]()
则观测数据的似然函数为:![]()
即: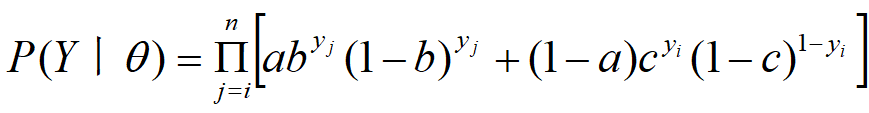
考虑求模型参数θ=(a,b,c)的极大似然估计,即:![]()
这个问题没有解析解,只能通过迭代的方法求解。EM算法就是可以用于求解这个问题的一种迭代
算法,下面给出针对以上问题的EM算法:
EM算法首先选取参数的初值,记作:![]()
然后通过下面的步骤迭代计算参数的估计值,直至收敛为止。第i次迭代参数的估计值为:
![]()
EM算法的第i+1次迭代如下:
①E步:计算在模型参数![]() 下观测数据
下观测数据![]() 来自掷硬币B的概率:
来自掷硬币B的概率:
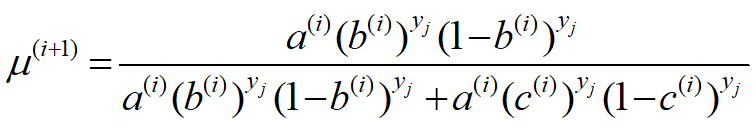
计算似然函数的期望: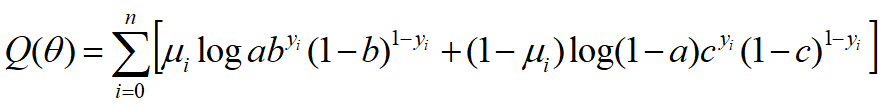
②M步:求似然函数的极大值
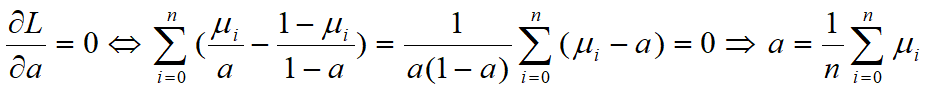
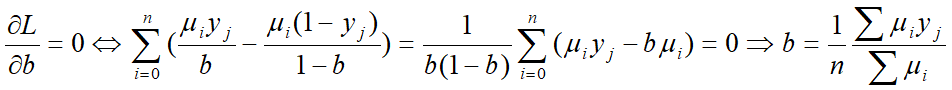

计算模型参数的新估计值:
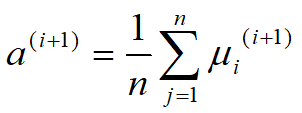
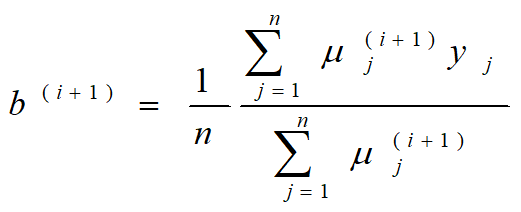
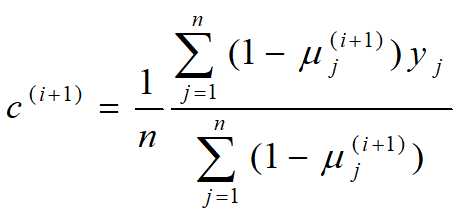
进行数字计算:假设模型参数的初始值取为:![]() 由E步第一个公式,
由E步第一个公式,
对y=0与y=1均有![]() ,利用迭代公式(新估计值),得到
,利用迭代公式(新估计值),得到![]()
由E步第一个公式有![]() ,j=1,2,3...10,继续迭代得
,j=1,2,3...10,继续迭代得![]() 。
。
于是参数模型的极大似然估计:![]() 。
。
3. EM算法步骤
EM算法的实现思路:首先根据已经给出的观测数据,估计出模型参数的值; 然后再依据上⼀
步估计出的参数值估计缺失数据的值,再根据估计出的缺失数据加上之前已经观测到的数据重新再
对参数值进行估计;然后反复迭代,直至最后收敛,迭代结束。
EM算法计算流程:
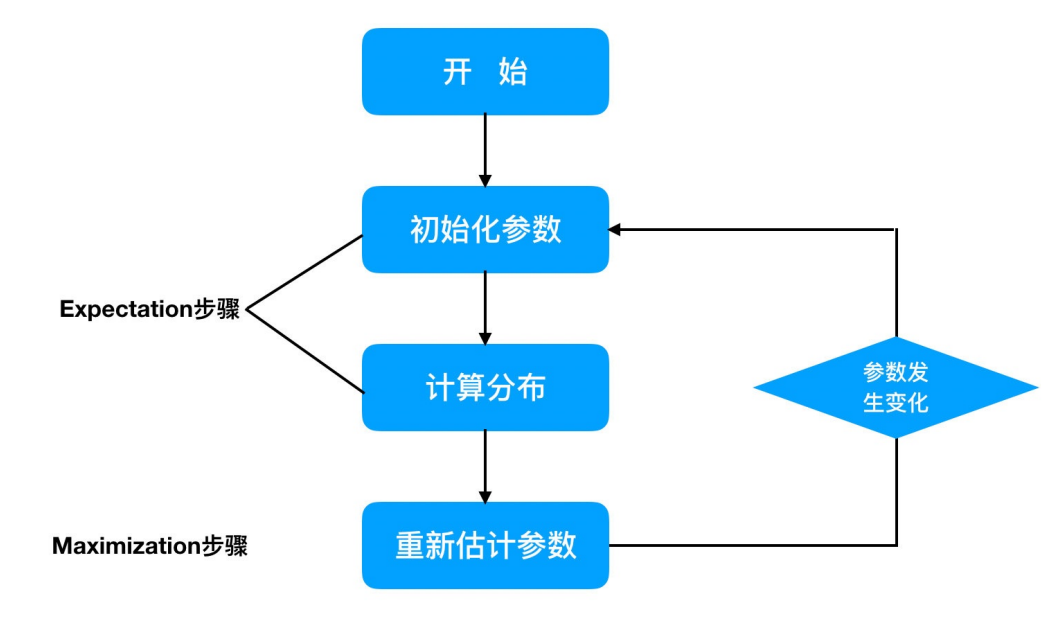
EM算法步骤:
选择模型参数的初值![]() ,开始迭代;
,开始迭代;
E步:记![]() 为第i次迭代参数θ的估计值,在第i+1次迭代的E步,定义Q函数并计算:
为第i次迭代参数θ的估计值,在第i+1次迭代的E步,定义Q函数并计算:
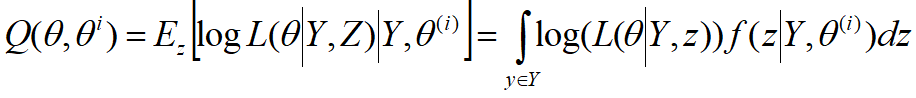
这里,Q函数定义为完全数据的对数似然函数![]() 在给定观测数据Y和当前的参
在给定观测数据Y和当前的参![]()
下对未观测数据Z的条件概率分布![]() 的期望;通过求期望,去掉了完整似然函数中的
的期望;通过求期望,去掉了完整似然函数中的
变量Z。其实就是用这个缺失数据的期望值来代替缺失的数据,而这个缺失的数据期望值和它的概
率分布有关。那么我们可以通过对似然函数关于缺失数据期望的最大化,来逼近原函数的极大值。
EM算法本质就是含有隐变量的概率模型参数的极大似然估计法。即EM的E步。
M步:求使![]() 极大化的θ,确定第i+1次迭代的参数的估计值
极大化的θ,确定第i+1次迭代的参数的估计值![]()
![]()
重复E、M两步,直到收敛。每次参数更新会增加非完整似然值,反复迭代后,会收敛到似然的局
部最大值。
4. EM算法原理
EM算法是一种解决存在隐含变量优化问题的有效方法。它的具体思想是:既然不能直接最大化参
数似然函数L,我们可以不断地建立参数似然函数L的下界(E步),然后优化下界(M步)。
利用琴生不等式得到似然函数的下界:
![]()

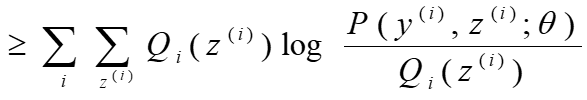
对于每一个样例i,让Qi表示该样例隐含变量z的某种分布,Qi满足条件:![]()
![]()
这个过程可以看作是对L(θ)求了下界。对于![]() 的选择有很多种,哪种更好呢?假设θ已经给
的选择有很多种,哪种更好呢?假设θ已经给
定,那么L(θ)的值就决定于![]() 和
和![]() 。我们可以通过调整这两个概率使下界不断上
。我们可以通过调整这两个概率使下界不断上
升,以逼近L(θ)的真实值,那么什么时候算是调整好了呢?当不等式变成等式时,说明调整后的
概率能够等价L(θ)。根据琴生不等式,等式成立的条件是随机变量取值为常数值,故可得到:
 c为常数,不依赖于
c为常数,不依赖于![]() 。
。
由于![]() ,那么就有
,那么就有![]() (多个等式分子分母相加不变,这个认为每
(多个等式分子分母相加不变,这个认为每
个样例的两个概率比值都是c),那么有:

将![]() 带入前面得到的似然函数下界,可以发现L(θ)的下界函数就是前面定义的
带入前面得到的似然函数下界,可以发现L(θ)的下界函数就是前面定义的![]()
函数。 这一步是E步,建立了L(θ)的下界。
接下来是M步,就是在给定![]() 后,调整θ,去极大化L(θ)的下界,那么怎么确保EM收敛
后,调整θ,去极大化L(θ)的下界,那么怎么确保EM收敛
呢?又如何确保每次迭代都能使极大似然估计单调增加呢?下述两个定理表明了利用EM算法所得
到的估计序列具有良好的收敛性,且其收敛到p(θ丨Y)的最大值。
定理1:设P(Y丨θ)为观测数据的似然函数,![]() (i=1,2...)为EM算法得到的参数估计序列,
(i=1,2...)为EM算法得到的参数估计序列,
![]() (i=1,2...)为对应的似然函数序列,则
(i=1,2...)为对应的似然函数序列,则![]() 是单调递增的,即
是单调递增的,即
![]() 。保证了EM算法的每次迭代都使似然函数增大或达到局部极值。
。保证了EM算法的每次迭代都使似然函数增大或达到局部极值。
定理2:设![]() 为观测数据的对数似然函数
为观测数据的对数似然函数![]() (i=1,2...)为EM算法得到的参数估计序列,
(i=1,2...)为EM算法得到的参数估计序列,![]() (i=1,2...)为对应的对数似然序列。
(i=1,2...)为对应的对数似然序列。
(1)如果P(Y丨θ)有上界,则![]() 收敛到某一值
收敛到某一值![]()
(2)在函数![]() 与
与![]() 满足一定条件下,由EM算法得到的参数估计序列
满足一定条件下,由EM算法得到的参数估计序列![]() 的收
的收
敛值![]() 是
是![]() 的稳定点。
的稳定点。
保证了EM算法所得到的估计序列具有良好的收敛性,且其收敛到p(θ丨Y)的最大值。
5. EM算法补充
EM算法的另一种理解:坐标上升法
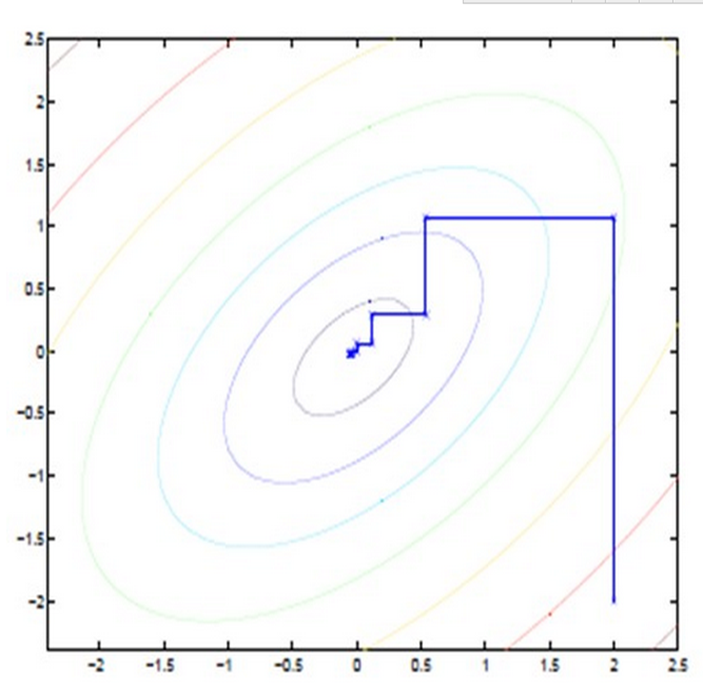
下图的直线式迭代优化的路径,可以看到每一步都会向最优值前进一步,而且前进路线是平行于坐
标轴的,因为每一步只优化一个变量。就像在x-y坐标系中找一个曲线的极值,然而曲线函数不能
直接求导,因此什么梯度下降方法就不适用了。但固定一个变量后,另外一个可以通过求导得到,
因此可以使用坐标上升法,一次固定一个变量,对另外的求极值,最后逐步逼近极值。对应到EM
上,E步:固定θ,优化Q;M步:固定Q,优化θ;交替将极值推向最大。
EM算法的几点说明:
①参数的初值可以任意选择,但需要注意EM算法对初值是敏感的。
②E步求Q函数。Q函数式中Z是未观测数据,Y是观测数据。注意,![]() 的第一个变元表
的第一个变元表
示要极大化的参数,第二个变元表示参数的当前估计值。每次迭代实际在求Q函数及其极大。
③M步求![]() 的极大化,得到
的极大化,得到![]() ,完成一次迭代
,完成一次迭代![]() 。每次迭代都使似
。每次迭代都使似
然函数增大或达到局部极值。
④给出停止迭代的条件,一般是对较小的正数![]() ,若满足以下条件,则停止迭代。
,若满足以下条件,则停止迭代。
![]()