一、堆介绍
1、定义
堆是一种图的树形结构,被用于实现“优先队列”(priority queues)。优先队列是一种数据结构,可以自由添加数据,但取出数据时要从最小值开始按顺序取出。在堆的树形结构中,各个顶点被称为“结点”(node),数据就存储在这些结点中,堆有下列特点:
(1)每个节点最多有两个子节点;
(2)堆列顺序必须从上到下,同一行从左到右;
(3)堆中某个节点的值总是不大于或不小于其父节点的值;
(4)存放数据时,一般会把新数据放在最下面一行靠左的位置。如果最下面一行没有多余 空间时,就在往下另起一行,并把数据添加到这一行的最左端。
2、堆的性质
(1)堆是一个完全二叉树;
(2)堆中某个结点的值总是不大于或不小于其父节点的值;
(a) 将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。常见的 堆有二叉堆、斐波那契堆等。
(b) 一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编 号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同, 则这棵二叉树称为完全二叉树。
(c) 一棵深度为k且有
个结点的二叉树称为满二叉树。也就是说除了叶子节点都有2个 子节点,且所有的叶子节点都在同一层。

(3)大顶堆与小顶堆的push与pop
大顶堆的push--往已有的大顶堆中添加元素
(a)将新元素作为树的最后一个节点
(b)比较新节点与其父节点:如果新节点的值大于父节点,那么交换父节点和新节点的值,其实就是就是交换两个元素的值
(c)重复上述步骤,直到新节点比其父节点小,或者当前新节点的位置已经是根节点了,那么停止上述循环即可,此时大顶堆更新完毕。
大顶堆的pop--弹出堆的根节点,然后对堆进行调整。
(a)将堆的最后一个叶子节点移到根节点的位置
(b)从根节点开始,比较根节点和其左右子节点的元素大小,若根节点不是都比子节点大,那么根节点与其较大的一个子节点进行交换
(c)只要存在子节点,那么继续比较父节点和左右子节点的大小,直到当前节点已经是叶子节点或者它比它的左右子节点取值都大,那么停止循环,最大堆已经更新完毕
3、优缺点及使用场景
优点:高效的插入和删除操作、有效的查找最值
缺点:不支持快速查找、不支持动态调整大小
使用场景:优先级队列、求最值、排序算法、调度算法、求中文数,总的来说,堆适合于处理需要高效地插入、删除最值的场景,但不适合需要频繁查找非最值元素的场合。
4、常用操作
push--插入元素道优先级列表中。
pop--从优先级列表中删除顶部元素。
top--返回优先级队列的顶部元素。
emplace--在优先级队列中直接构造元素。
swap--交换两个优先级队列的内容。
二、面试常考的算法
1、最小的K个数
题目:给定一个长度为n的可能有重复值的数组,找出其中不去重的最小的k个数。
示例:input:[4,5,1,6,2,7,3,8] ,k = 4;output:[1,2,3,4]
思路:求最小的K个数和求最大的K个数都可以通过维护堆的方式来进行完成。
最小的K个数:维护大顶堆,陆续往里面插入元素,当堆的长度大于K时,弹出堆顶元素,最后得到的就是K个数组中最小的元素。
最大的K个数:同理,维护小顶堆。
C++中的堆创建:
(1)std::priority_queue<int> pq; //创建大顶堆
(2)std::priority_queue<int, std::vector<int>, std::greater<int>> pq; //创建小顶堆
参数1:指定了存储的元素类型为整数
参数2:使用vector作为底层容器来存储元素
参数3:std::greater<int>是一个比较函数,定义了元素的优先级比较方式。
(3)自定义优先级
struct node
{int priority;
int value;friend bool operator< (node n1, node n2)
{
return n1.priority < n2.priority;
}
};
python中的堆创建:
from queue import PriorityQueue
pq = PriorityQueue() # 默认最小堆
python中最大堆的创建:通过将元素的优先级取相反数来实现。这样,最大的元素实际上会变成优先级最高的负数,因此会被优先弹出。
for i in array:# 添加元素,注意元素的优先级是取相反数
pq.put((-i, i))
if(pq.qsize() > k):
# 弹出元素
pq.get()
#include<vector>
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
vector<int> getLeastNumbers(vector<int> array, int k){
vector<int> res;
priority_queue<int> heap; //大顶堆
// priority_queue<int, vector<int>,greater<int>> heap; //小顶堆
for(int i = 0; i < array.size(); i++){
heap.push(array[i]);
if(heap.size() > k) heap.pop();
}
while(heap.size()){
res.push_back(heap.top());
heap.pop();
}
reverse(res.begin(),res.end());
return res;
}
int main(){
vector<int> array = {4, 5, 1, 6, 2, 7, 3, 8};
int k = 4;
vector<int> res = getLeastNumbers(array, k);
for(auto r: res){
cout << r << ',';
}
} 
2、第K大的数
题目:给定一个长度为n的可能有重复值的数组,找出其中不去重的最大的第k个数。
示例:input:[4,5,1,6,2,7,3,8] ,k = 4;output:5
思路:求最小的K个数和求最大的K个数都可以通过维护堆的方式来进行完成。
方法1:(大顶堆)同上述第一题,使用大顶堆的方式进行完成,注意到这题给的参数中有一个总数(数组的总数),利用大顶堆,他要我们求第K大,那我们反向求n-k+1小就行。
方法2:(小顶堆),利用小顶堆,求第K大。
#include<vector>
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
// 小顶堆实现
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int, vector<int>, greater<int>> Q;
for (auto x : nums) {
Q.push(x);
// cout << Q.top() << ",";
if(Q.size() > k) Q.pop();
}
return Q.top();
}
// 大顶堆实现
int getKth(vector<int> a, int n, int k){
priority_queue<int> heap; //大顶堆
for(int i = 0; i < a.size(); i++){
heap.push(a[i]);
if(heap.size() > n-k+1) heap.pop();
}
int result = heap.top();
return result;
}
int main(){
vector<int> array = {4, 5, 1, 6, 2, 7, 3, 8};
int k = 3;
int res = findKthLargest(array, k);
cout << res<<endl;
int res2 = getKth(array, array.size(), k);
cout << res2;
}
3、数据流中的中位数
题目:给定一个长度为n的可能有重复值的数组,计算这组数的中位数。
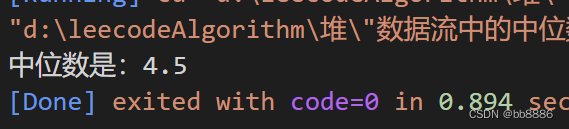
示例:input:[4,5,1,6,2,7,3,8] ,output:4.5
input:[4,5,1,6,2,7,3,8,9] ,output:5
思路:方法1:利用堆排序将给定数组排序,排好序后在去找中位数。
方法2:同第2题的思路,只需利用堆找到中位数索引对应的元素计算即可。
#include<vector>
#include<queue>
#include<iostream>
using namespace std;
vector<int> GetMedianInData(vector<int> arr){
priority_queue<int> pq;
vector<int> res;
for(auto c: arr){
pq.push(c);
}
while(pq.size()){
res.push_back(pq.top());
pq.pop();
}
return res;
}
// 小顶堆实现
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int, vector<int>, greater<int>> Q;
for (auto x : nums) {
Q.push(x);
// cout << Q.top() << ",";
if(Q.size() > k) Q.pop();
}
return Q.top();
}
int main(){
// 先堆排序,再找中位数
// vector<int> array = {4, 5, 1, 6, 2, 7, 3, 8, 9};
// vector<int> res = GetMedianInData(array);
// for(auto r: res){
// cout << r << ',';
// }
// double median;
// if (res.size() % 2 == 1){
// median = res[res.size() / 2];
// }
// else{
// median = (double(res[res.size() / 2]) + double(res[res.size() / 2 - 1])) / 2;
// }
// cout << "中位数是:" << median;
// 把中位数对应的元素利用堆排序找出来
vector<int> array = {4, 5, 1, 6, 2, 7, 3, 8};
int median, front, behind;
double res;
if (array.size() % 2 == 1){
median = array.size() / 2;
res = findKthLargest(array, median + 1);
}
else{
front = array.size() / 2 ;
behind = array.size() / 2 - 1;
res = double(findKthLargest(array, behind + 1) + findKthLargest(array, front + 1))/2;
}
cout << "中位数是:" << res;
}