实验4 贝叶斯分类
一、实验目的
1. 了解并学习机器学习相关库的使用。
2. 熟悉贝叶斯分类原理和方法,并对MNIST数据集进行分类。
二、实验内容
1. 使用贝叶斯方法对mnist或mnist variation数据集进行分类,并计算准确率。数据集从网上下载(如百度飞桨平台)。
2. 改变算法参数,观察对识别准确率的影响。
三、实验环境
| 平台 | Jupyter Notebook (anaconda3) |
| Python版本 | python 3.9 |
| 第三方依赖 | numpy、scikit-learn、matplotlib |
四、方法流程
1:配置第三方依赖;
2:下载mnist数据集;
3:划分数据集为训练集train和测试集test;
4:调用机器学习库的贝叶斯分类模型;
5:设置pred为模型预测的结果;
6:比较test和pred,计算准确率;
7:输出测试集test的混淆矩阵;
8:按照上述方法继续对其他模型进行调参并对比模型的训练结果。
五、实验展示(训练过程和训练部分结果进行可视化)
1:三种贝叶斯模型的训练结果对比
| 模型 | 名称 | 分类准确率 |
| GaussianNB | 高斯Bayes算法 | 55.58% |
| MultinomialNB | 多项式Bayes算法 | 83.65% |
| BernoulliNB | 伯努利Bayes算法 | 84.13% |
可视化训练结果(混淆矩阵):
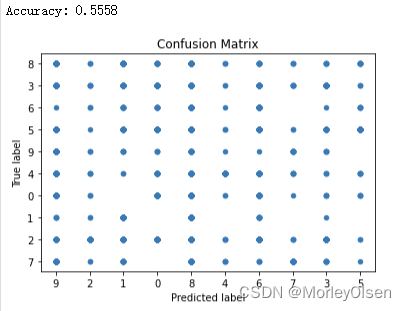
GaussianNB

MultinomialNB
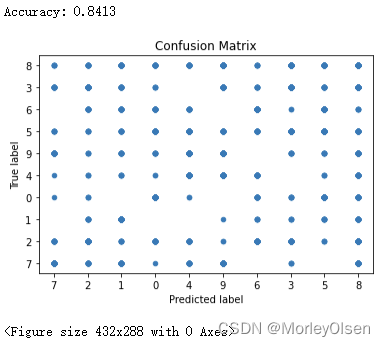
BernoulliNB
训练数据:

X = mnist.data(像素结果)

y = mnist.target(标签结果)
2:高斯Bayes算法(GaussianNB)在不同平滑参数下的训练结果对比
| 平滑参数var_smoothing | 分类准确率 |
| 0.95 | 74.97% |
| 0.8 | 75.89% |
| 0.5 | 77.91% |
| 0.3 | 79.77% |
| 0.05 | 81.40% |
| 不采用 | 55.58% |
3:高斯Bayes算法(GaussianNB)在设置均等先验概率下的训练结果

可以发现,与未设置priors参数时候的结果一致,说明模型预先就均分了先验概率。
4:伯努利Bayes算法(BernoulliNB)在是否禁用学习类的先验概率的训练结果对比
| 先验概率使用fit_prior | 分类准确率 |
| True | 84.13% |
| False | 84.15% |
5:伯努利Bayes算法(BernoulliNB)在不同加法(Laplace/Lidstone)平滑参数下的训练结果对比
| 平滑参数alpha | 分类准确率 |
| 0.1 | 84.15% |
| 0.5 | 84.14% |
| 0.9 | 84.14% |
6:伯努利Bayes算法(BernoulliNB)在不同二值化阈值参数下的训练结果对比
| 二值化阈值参数binarize | 分类准确率 |
| 0.0 | 84.13% |
| 0.5 | 84.13% |
| 1.0 | 84.13% |
7:多项式Bayes算法(MultinomialNB)在不同加法(Laplace/Lidstone)平滑参数下的训练结果对比
| 平滑参数alpha | 分类准确率 |
| 0.1 | 83.67% |
| 0.5 | 83.66% |
| 0.9 | 83.65% |
8:伯努利Bayes算法(BernoulliNB)在是否禁用学习类的先验概率的训练结果对比
| 先验概率使用fit_prior | 分类准确率 |
| True | 83.65% |
| False | 83.65% |
9:多项式Bayes算法(MultinomialNB)的单张图片测试结果

10:对数据集进行主成分分析、标准化和归一化处理后的训练结果
主成分分析:
| PCA_Transfer=PCA(n_components=0.95) PCA_x=PCA_Transfer.fit_transform(x) |
标准化:
| Standard_Transfer=StandardScaler() standard_x_train=Standard_Transfer.fit_transform(x_train) standard_x_test=Standard_Transfer.fit_transform(x_test) |
归一化:
| MinMax_Transfer=MinMaxScaler() Guiyihua_x_train=MinMax_Transfer.fit_transform(x_train) Guiyihua_x_test=MinMax_Transfer.fit_transform(x_test) |
经过上述操作后的模型训练结果:

| 模型 | 名称 | 分类准确率 |
| GaussianNB | 高斯Bayes算法 | 77.49% |
| MultinomialNB | 多项式Bayes算法 | 85.45% |
| BernoulliNB | 伯努利Bayes算法 | 74.14% |
六、实验结论
1:在GaussianNB中,我们可以改变的主要参数是priors和var_smoothing。priors参数可以手动设置每个类别的先验概率,默认让模型根据数据自动计算先验概率。var_smoothing参数用于控制对类别不确定性的处理方式。var_smoothing值过大,可能会让模型对实际数据中的变化不敏感,导致模型性能降低;var_smoothing值过小,可能会对数据中的噪声和异常值更敏感,导致训练数据过拟合。
2:在MultinomialNB中,我们可以改变的主要参数是alpha、fit_prior、class_prior和min_categories。加法平滑参数alpha用于处理因数据稀疏而在学习数据中未观察到的特征,防止概率计算时出现0值。是否学习类的先验概率fit_prior如果为假,使用均匀的先验概率,即认为所有输出类别的可能性相等。类别的先验概率class_prior如果指定,则不根据数据调整先验概率。指定每个特征的最小类别数min_categories帮助防止在特征维度非常高但训练样本相对较少时出现过拟合。
3:在BernoulliNB中,我们可以改变的主要参数是alpha、binarize、fit_prior和class_prior。与MultinomialNB相比,binarize是用于二值化输入特征的阈值。如果设定,则输入特征大于这个阈值的将会被二值化为1,否则二值化为0。
4:在模型选择方面,MultinomialNB和BernoulliNB更适合处理MNIST数据集,因为MNIST的图像可以表示为像素强度计数(适合多项式分布)或二值化的像素存在与否(适合伯努利分布)。GaussianNB可能在没有适当预处理(如归一化)的情况下表现不佳。
5:在使用贝叶斯分类器后,进行误差分析(比如混淆矩阵)可以揭示某些数字更难区分。数字之间难以区分通常是由贝叶斯模型的独立性假设造成的。
七、遇到的问题及其解决方案
问题1:安装第三方依赖时,显示pip有更新。
解决1:采用【pip install --upgrade pip】命令,升级pip即可。
问题2:Jupyter Notebook只显示ipykernel为python 3,不显示具体的python版本。
解决2:采用【!pip3 -V】命令进行查看,结果如下图所示。

八、附件
1:三类贝叶斯模型的基本调用源代码
| import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import fetch_openml
# 加载MNIST或MNIST Variation数据集 mnist = fetch_openml('mnist_784', version=1) X, y = mnist.data, mnist.target X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] # 训练贝叶斯分类器 from sklearn.naive_bayes import GaussianNB gnb = GaussianNB() gnb.fit(X_train, y_train)
# 预测测试集 y_pred = gnb.predict(X_test)
# 计算准确率 acc = np.sum(y_pred == y_test) / len(y_test) print("Accuracy:", acc)
# 可视化结果 plt.scatter(y_pred, y_test, s=20) plt.xlabel("Predicted label") plt.ylabel("True label") plt.title("Confusion Matrix") plt.show() plt.savefig('ret.png') # 训练贝叶斯分类器 from sklearn.naive_bayes import MultinomialNB gnb1 = MultinomialNB() gnb1.fit(X_train, y_train)
# 预测测试集 y_pred = gnb1.predict(X_test)
# 计算准确率 acc = np.sum(y_pred == y_test) / len(y_test) print("Accuracy:", acc)
# 可视化结果 plt.scatter(y_pred, y_test, s=20) plt.xlabel("Predicted label") plt.ylabel("True label") plt.title("Confusion Matrix") plt.show() plt.savefig('ret1.png') # 训练贝叶斯分类器 from sklearn.naive_bayes import BernoulliNB gnb2 = BernoulliNB() gnb2.fit(X_train, y_train)
# 预测测试集 y_pred = gnb2.predict(X_test)
# 计算准确率 acc = np.sum(y_pred == y_test) / len(y_test) print("Accuracy:", acc)
# 可视化结果 plt.scatter(y_pred, y_test, s=20) plt.xlabel("Predicted label") plt.ylabel("True label") plt.title("Confusion Matrix") plt.show() plt.savefig('ret2.png') |
2:单张图片对模型进行测试的代码
| import matplotlib.pyplot as plt from sklearn.datasets import fetch_openml from sklearn.model_selection import train_test_split from sklearn.naive_bayes import GaussianNB from sklearn.metrics import accuracy_score from skimage import io, color, filters from skimage.transform import resize import numpy as np # 训练贝叶斯分类器 from sklearn.naive_bayes import MultinomialNB gnb = MultinomialNB() gnb.fit(X_train, y_train) # 读取图像文件 image_path = r'C:\Users\86158\Desktop\train_labels\train_examples_labels\train_new\5.png' image = io.imread(image_path) # 将图像缩放到28x28像素 scaled_image = resize(image, (28, 28), anti_aliasing=True) # 将图像数据转换为一维数组 flat_image = scaled_image.flatten() # 将像素值缩放到0到1(如果你的模型是在这个范围的数据上训练的) processed_image = flat_image / 255.0 # 确保这里的processed_image具有与模型训练数据相同的形状 # 如果是MNIST,它应该有784个特征 processed_image = processed_image.reshape(1, -1) # 使用模型进行预测 prediction = gnb.predict(processed_image) print(f"Predicted class for the input image: {prediction[0]}") # 可选:显示图像 plt.imshow(scaled_image, cmap='gray') plt.title(f'Predicted Class: {prediction[0]}') plt.show() |
3:对数据集进行主成分分析、标准化和归一化处理的完整代码
| from sklearn.datasets import fetch_openml from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler from sklearn.decomposition import PCA from sklearn.neighbors import KNeighborsClassifier from sklearn.naive_bayes import MultinomialNB,GaussianNB,BernoulliNB import matplotlib.pyplot as plt from sklearn.preprocessing import MinMaxScaler from sklearn.model_selection import GridSearchCV from sklearn.tree import DecisionTreeClassifier from sklearn.tree import plot_tree from sklearn.tree import export_graphviz from sklearn.ensemble import RandomForestClassifier from sklearn.linear_model import LogisticRegression from sklearn.model_selection import learning_curve from sklearn.metrics import classification_report import numpy as np mnist=fetch_openml("mnist_784",version=1,cache=True) x=mnist.data y=mnist.target # 对输入特征进行主成分分析降维 print("降维前的特征数:",x.shape[1]) PCA_Transfer=PCA(n_components=0.95) PCA_x=PCA_Transfer.fit_transform(x) print("降维后的特征数:",PCA_x.shape[1]) # 划分训练集和测试集 x_train,x_test,y_train,y_test=train_test_split(PCA_x,y,test_size=0.2,random_state=1) # 对输入特征值进行标准化处理 Standard_Transfer=StandardScaler() standard_x_train=Standard_Transfer.fit_transform(x_train) standard_x_test=Standard_Transfer.fit_transform(x_test) # 对输入特征值进行归一化处理 MinMax_Transfer=MinMaxScaler() Guiyihua_x_train=MinMax_Transfer.fit_transform(x_train) Guiyihua_x_test=MinMax_Transfer.fit_transform(x_test) Bayes_estimator1=MultinomialNB() param_dic={"alpha":[0.5,0.6,0.7,0.8,0.9,1,1.1,1.2]} Bayes_estimator1=GridSearchCV(Bayes_estimator1,param_grid=param_dic,cv=10,n_jobs=-1) Bayes_estimator1.fit(Guiyihua_x_train,y_train) print("多项式Bayes算法在测试集上的平均预测成功率:",Bayes_estimator1.score(Guiyihua_x_test,y_test)) Bayes_estimator2=GaussianNB() Bayes_estimator2=GridSearchCV(Bayes_estimator2,cv=10,param_grid={},n_jobs=-1) Bayes_estimator2.fit(x_train,y_train) print("高斯Bayes算法在测试集上的平均预测成功率:",Bayes_estimator2.score(x_test,y_test)) Bayes_estimator3=BernoulliNB() Bayes_estimator2=GridSearchCV(Bayes_estimator2,cv=10,param_grid={},n_jobs=-1) Bayes_estimator3.fit(x_train,y_train) print("伯努利Bayes算法在测试集上的平均预测成功率:",Bayes_estimator3.score(x_test,y_test)) |





![P1025 [NOIP2001 提高组] 数的划分](https://img-blog.csdnimg.cn/direct/a0d5f18eb6a84e9fa3667dded9da1075.png)