实验3 蚁群算法的应用
一、实验内容
TSP 问题的蚁群算法实现。
二、实验目的
1. 熟悉和掌握蚁群算法的基本概念和思想;
2. 理解和掌握蚁群算法的参数选取,解决实际应用问题。
三、实验原理
1.算法来源
蚁群算法的基本原理来源于自然界蚂蚁觅食的最短路径原理,它可以在没有任何提示的情况下找到从食物源到巢穴的最短路径,并且能在环境发生变化(如原有路径上有了障碍物)后,自适应地搜索新的最佳路径。
2.原理
正反馈:
单个的蚂蚁为了避免自己迷路,它在爬行时,同时也会释放一种特殊的分泌物——信息素(Pheromone),而且它也能觉察到一定范围内的其它蚂蚁所分泌的信息素,并由此影响它自己的行为。当一条路上的信息素越来越多(当然,随着时间的推移会逐渐减弱),后来的蚂蚁选择这条路径的概率也就越来越大,从而进一步增加了该路径的信息素浓度。
多样性:
同时为了保证蚂蚁在觅食的时候不至走进死胡同而无限循环,蚂蚁在寻找路径的过程中,需要有一定的随机性,虽然在觅食的过程中会根据信息素的浓度去觅食,但是有时候也有判断不准,环境影响等其他很多种情况,还有最终要的一点就是当前信息素浓度大的路径并不一定是最短的路径,需要不断的去修正,多样性保证了系统的创新能力。
正是这两点的巧妙结合才使得蚁群的智能行为涌现出来。
3.具体实现需要解决的两个首要问题
(1)如何实现单个蚂蚁寻路的过程;
(2)如何实现信息素浓度的更新。
四、实验要求
1.在3个不同城市规模(如30个城市,50个城市,100个城市)的条件下,可多次运行,编程利用蚁群算法寻找TSP问题的最短路径。
为探究蚁群算法的基本结果,本实验【1】中的测试环境中的各类参数依次是: 迭代次数max_iter = 200、信息素影响因子alpha = 2、距离影响因子beta = 5、信息素挥发速率rho = 0.5、信息素强度q = 100。
代码中展现如下:
| num_cities, distance_matrix, num_ants, max_iter=200, alpha=2, beta=5, rho=0.5, q=100 |
为更好地展示不同城市规模下的运行结果,本实验测试了共9次独立的运行结果(每种情况3次),并制作表1.a至表1.c,分别描述城市规模在30、50、100情况下的运行时间和适应度。汇总结果如表1所示,各类城市规模情况下的ACO解决TSP的可视化图像示例如图1至图3所示。
图1. 城市规模为30时,ACO解决TSP的可视化图像示例

图2. 城市规模为50时,ACO解决TSP的可视化图像示例

图3. 城市规模为100时,ACO解决TSP的可视化图像示例

表1. 蚁群算法求解不同规模的TSP问题的结果
| 城市规模 | 最好适应度 | 平均适应度 | 平均运行时间 |
| 30 | 483.71 | 484.61 | 14.67 |
| 50 | 609.19 | 615.07 | 58.80 |
| 100 | 806.80 | 828.73 | 506.89 |
表1.a. 当城市规模为30时,不同次运行情况下的结果
| 运行次数序号 | 输出的距离最优解 | 输出的运行时间/s |
| 1 | 489.61 | 15.03 |
| 2 | 483.71 | 14.40 |
| 3 | 485.50 | 14.58 |
| 平均结果 | 484.61 | 14.67 |
表1.b. 当城市规模为50时,不同次运行情况下的结果
| 运行次数序号 | 输出的距离最优解 | 输出的运行时间/s |
| 1 | 615.44 | 58.95 |
| 2 | 620.58 | 58.39 |
| 3 | 609.19 | 59.06 |
| 平均结果 | 615.07 | 58.80 |
表1.c. 当城市规模为100时,不同次运行情况下的结果
| 运行次数序号 | 输出的距离最优解 | 输出的运行时间/s |
| 1 | 806.80 | 505.75 |
| 2 | 831.36 | 511.10 |
| 3 | 848.04 | 503.83 |
| 平均结果 | 828.73 | 506.89 |
2.调试代码,列表比较蚁群算法设定不同参数时的计算结果。
为更好地展示不同参数(信息素因子、启发函数因子、信息素常数、信息素挥发因子、蚁群数量)下的运行结果,本实验确定城市规模为30且迭代次数为200,测试了共33次独立的运行结果(每种情况3次),并制作表2.a至表2.k,分别描述表2中各种情况下的最优解、运行时间和适应度。
表2. 不同参数的求解结果
| 蚁群数量 | 信息素因子α | 启发函数因子β | 信息素常数Q | 信息素挥发因子ρ | 最好适应度 | 平均适应度 |
| 45 | 2 | 5 | 100 | 0.5 | 483.71 | 484.61 |
| 45 | 1 | 5 | 100 | 0.5 | 479.21 | 482.21 |
| 45 | 4 | 5 | 100 | 0.5 | 483.71 | 494.72 |
| 45 | 2 | 3 | 100 | 0.5 | 483.71 | 484.30 |
| 45 | 2 | 10 | 100 | 0.5 | 483.71 | 488.59 |
| 45 | 2 | 5 | 10 | 0.5 | 486.90 | 490.61 |
| 45 | 2 | 5 | 1000 | 0.5 | 490.03 | 490.84 |
| 45 | 2 | 5 | 100 | 0.1 | 483.71 | 493.52 |
| 45 | 2 | 5 | 100 | 0.8 | 483.71 | 485.81 |
| 10 | 2 | 5 | 100 | 0.5 | 491.76 | 503.46 |
| 70 | 2 | 5 | 100 | 0.5 | 483.71 | 483.71 |
表2.a. 当蚁群数量为45、信息素因子为2、启发函数因子为5、信息素常数为100、信息素挥发因子为0.5时,不同次运行情况下的结果
| 运行次数序号 | 输出的距离最优解 | 输出的运行时间/s |
| 1 | 489.61 | 15.03 |
| 2 | 483.71 | 14.40 |
| 3 | 485.50 | 14.58 |
| 平均结果 | 484.61 | 14.67 |
表2.b. 当蚁群数量为45、信息素因子为1、启发函数因子为5、信息素常数为100、信息素挥发因子为0.5时,不同次运行情况下的结果
| 运行次数序号 | 输出的距离最优解 | 输出的运行时间/s |
| 1 | 479.21 | 14.57 |
| 2 | 483.71 | 15.29 |
| 3 | 483.71 | 15.15 |
| 平均结果 | 482.21 | 15.00 |
表2.c. 当蚁群数量为45、信息素因子为4、启发函数因子为5、信息素常数为100、信息素挥发因子为0.5时,不同次运行情况下的结果
| 运行次数序号 | 输出的距离最优解 | 输出的运行时间/s |
| 1 | 485.50 | 14.61 |
| 2 | 514.95 | 14.25 |
| 3 | 483.71 | 14.20 |
| 平均结果 | 494.72 | 14.35 |
表2.d. 当蚁群数量为45、信息素因子为2、启发函数因子为3、信息素常数为100、信息素挥发因子为0.5时,不同次运行情况下的结果
| 运行次数序号 | 输出的距离最优解 | 输出的运行时间/s |
| 1 | 483.71 | 14.71 |
| 2 | 483.71 | 14.95 |
| 3 | 485.50 | 14.69 |
| 平均结果 | 484.30 | 14.78 |
表2.e. 当蚁群数量为45、信息素因子为2、启发函数因子为10、信息素常数为100、信息素挥发因子为0.5时,不同次运行情况下的结果
| 运行次数序号 | 输出的距离最优解 | 输出的运行时间/s |
| 1 | 492.47 | 14.23 |
| 2 | 489.61 | 14.14 |
| 3 | 483.71 | 13.96 |
| 平均结果 | 488.59 | 14.11 |
表2.f. 当蚁群数量为45、信息素因子为2、启发函数因子为5、信息素常数为10、信息素挥发因子为0.5时,不同次运行情况下的结果
| 运行次数序号 | 输出的距离最优解 | 输出的运行时间/s |
| 1 | 492.47 | 14.14 |
| 2 | 492.47 | 14.35 |
| 3 | 486.90 | 14.42 |
| 平均结果 | 490.61 | 14.30 |
表2.g. 当蚁群数量为45、信息素因子为2、启发函数因子为5、信息素常数为1000、信息素挥发因子为0.5时,不同次运行情况下的结果
| 运行次数序号 | 输出的距离最优解 | 输出的运行时间/s |
| 1 | 490.03 | 14.56 |
| 2 | 490.03 | 14.67 |
| 3 | 492.47 | 14.59 |
| 平均结果 | 490.84 | 14.60 |
表2.h. 当蚁群数量为45、信息素因子为2、启发函数因子为5、信息素常数为100、信息素挥发因子为0.1时,不同次运行情况下的结果
| 运行次数序号 | 输出的距离最优解 | 输出的运行时间/s |
| 1 | 498.50 | 14.34 |
| 2 | 483.71 | 13.86 |
| 3 | 498.37 | 14.04 |
| 平均结果 | 493.52 | 14.08 |
表2.i. 当蚁群数量为45、信息素因子为2、启发函数因子为5、信息素常数为100、信息素挥发因子为0.8时,不同次运行情况下的结果
| 运行次数序号 | 输出的距离最优解 | 输出的运行时间/s |
| 1 | 483.71 | 14.12 |
| 2 | 483.71 | 13.85 |
| 3 | 490.03 | 13.89 |
| 平均结果 | 485.81 | 13.95 |
表2.j. 当蚁群数量为10、信息素因子为2、启发函数因子为5、信息素常数为100、信息素挥发因子为0.5时,不同次运行情况下的结果
| 运行次数序号 | 输出的距离最优解 | 输出的运行时间/s |
| 1 | 491.76 | 3.25 |
| 2 | 516.42 | 3.19 |
| 3 | 502.22 | 3.24 |
| 平均结果 | 503.46 | 3.22 |
表2.k. 当蚁群数量为70、信息素因子为2、启发函数因子为5、信息素常数为100、信息素挥发因子为0.5时,不同次运行情况下的结果
| 运行次数序号 | 输出的距离最优解 | 输出的运行时间/s |
| 1 | 483.71 | 23.05 |
| 2 | 483.71 | 22.1 |
| 3 | 483.71 | 22.34 |
| 平均结果 | 483.71 | 22.49 |
3.比较与实验2中遗传算法的效果差异。
收敛速度:遗传算法通常在早期迭代中快速找到较好的解,而蚁群算法可能需要更多的迭代次数。
执行效率:遗传算法在每一代中进行种群评估、选择、交叉和变异,其执行效率取决于种群规模和所选操作的复杂性。而蚁群算法通常在执行过程中涉及较多的局部搜索和信息素更新,这可能使得每次迭代的计算更加密集。
解的质量:蚁群算法倾向于更加稳健地搜索解空间,而遗传算法可能更快地收敛到一个解,但可能是局部最优解。
参数敏感性:两种算法都对参数设置敏感,但遗传算法需要更细致的参数调整。
稳定性与一致性:遗传算法由于其随机性较高(特别是在交叉和变异过程中),在不同的运行中可能产生较大的结果差异。而蚁群算法在不同运行中的表现可能更加一致,由于其搜索机制倾向于逐渐积累解决方案。
问题规模适应性:遗传算法在小至中等规模的TSP问题上效果较好,但是需要重新初始化或通过其他机制引入新的遗传多样性;而蚁群算法在大规模问题上表现更优,对于动态变化的环境有很好的适应性,能够有效地调整已有路径的信息素浓度。
4.总结与讨论。
【1】关键参数的选取。
根据上面的实验结果,我们可以得到以下参数及其选择情况可能导致的结果,并总结出一般情况下的参数选择范围。
| 参数名称 | 极端情况会导致的结果 | 一般情况的选择范围 |
| 蚂蚁数目m | 过大:信息素变化趋于平均 过小:未搜索路径信息素提前减到0 | m=1.5M,M是城市数量 |
| 信息素因子α | 过大:选择走以前的路径概率大 过小:提前局部最优 | α=[1,4] |
| 启发函数因子β | 过大:提前局部最优 过小:随机搜索 | β=[3,4.5] |
| 信息素挥发因子ρ | 过大:信息素快速挥发,迭代搜索没有记忆,最后随机搜索 过小:信息素累积,提前局部最优 | ρ=[0.2,0.5] |
| 信息素常数Q | 越大:已遍历路径的信息素积累越快,有利于收敛 | Q=[10,1000] |
| 最大迭代次数epoch | 过大:资源浪费 过小:算法未收敛就结束 | epoch=[100,500] |
【2】蚁群算法的基本思想和流程图
流程图:
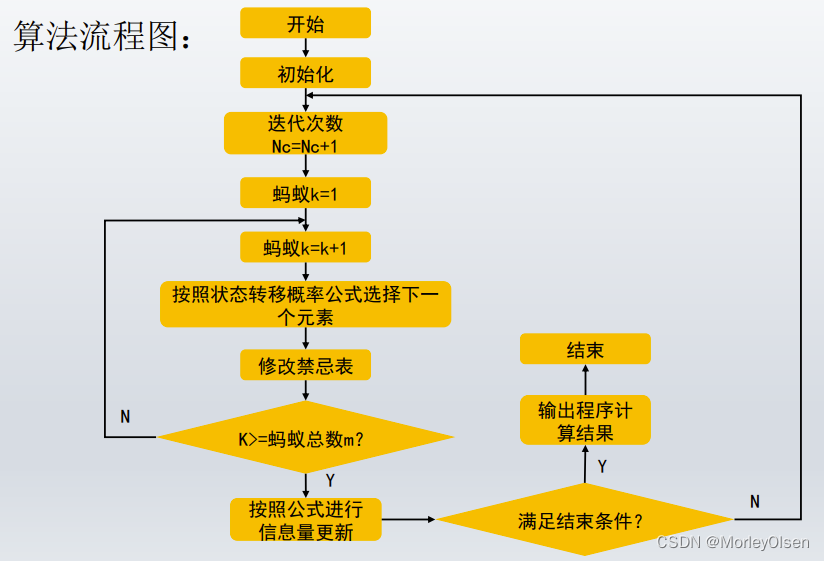
基本思想:
1:根据具体问题设置多只蚂蚁,分头并行搜索
2:每只蚂蚁完成一次周游后,在行进的路上释放信息素,信息素量与解的质量成正比
3:蚂蚁路径的选择根据信息素强度大小(初始信息素量设为相等),同时考虑两点之间的距离,采用随机的局部搜索策略。这使得距离较短的边,其上的信息素量较大,后来的蚂蚁选择该边的概率也较大
4:每只蚂蚁只能走合法路线(经过每个城市1次且仅1次),为此设置禁忌表来控制
5:所有蚂蚁都搜索完一次就是迭代一次,每迭代一次就对所有的边做一次信息素更新,原来的蚂蚁死掉,新的蚂蚁进行新一轮搜索
6:更新信息素包括原有信息素的蒸发和经过的路径上信息素的增加
7:达到预定的迭代步数,或出现停滞现象(所有蚂蚁都选择同样的路径,解不再变化),则算法结束,以当前最优解作为问题的解输出
【3】蚁群算法是一种本质上并行的算法。每只蚂蚁搜索的过程彼此独立,仅通过信息激素进行通信。蚁群算法在问题空间的多点同时开始进行独立的解搜索,不仅增加了算法的可靠性,也使得算法具有较强的全局搜索能力。但是也正是由于其并行性的本质,蚁群算法的搜索时间较长,在求解小规模的NP问题时耗费的计算资源相比其他启发式算法要多,因而显得效率很低下。
【4】蚁群算法的三个要素
1:蚁群活动
2:信息素挥发
3:信息素增加
【5】蚁群算法的主要体现
1:转移概率公式
2:信息素更新公式
五、遇到的问题及其解决方案
问题1:距离矩阵中,起初只是对从i点到i点的距离设置为0,这样会导致重复选择,失去了禁忌表的功能。
解决1:后续将matrix的主对角线的值更新为numpy中的inf值,即无穷大的值。
问题2:在设置rho = 0.9时,出现报错ValueError: probabilities contain NaN。
| c:\Users\86158\Desktop\实验3\test.py:102: RuntimeWarning: invalid value encountered in divide probabilities = probabilities / np.sum(probabilities) Traceback (most recent call last): File "c:\Users\86158\Desktop\实验3\test.py", line 149, in <module> best_route, best_distance = aco.solve() File "c:\Users\86158\Desktop\实验3\test.py", line 124, in solve next_city = self._choose_next_city(current_city, ant) File "c:\Users\86158\Desktop\实验3\test.py", line 104, in _choose_next_city return np.random.choice(range(self.num_cities), p=probabilities) File "mtrand.pyx", line 935, in numpy.random.mtrand.RandomState.choice ValueError: probabilities contain NaN |
解决2:这个警告出现在 probabilities = probabilities / np.sum(probabilities) 这一行。分析可知 np.sum(probabilities) 的结果是0,导致了一个除以0的操作。当概率之和为0时,除法会产生无效值(NaN)。这变相地说明了rho过大,会导致信息素挥发过快,导致算法的稳定性较差。
六、附件
蚁群算法源代码(含完整注释)
| import random import matplotlib.pyplot as plt import numpy as np import time # 确定随机数生成的种子 random.seed(40) # 城市数目 num = int(input("please input the number of cities: ")) # 开始计时 start = time.time() # 固定生成点数目 points = [] for i in range(num): # 随机生成x和y坐标 x = random.randint(0,100) y = random.randint(0,100) # 将随机坐标push到points里面 points.append((x,y)) print("检查初代点坐标:") print(points) # 计算初代点symmetric matrix的函数 def distance_matrix(points): # 初始化一个0 matrix matrix = np.zeros((num,num))
# 开始计算各点之间的距离 for i in range(num): for j in range(num): # 如果当前点=>当前点,则认为是infinite distance if i==j: matrix[i,j]=np.inf # 否则,计算两个点之间的欧式距离 else: matrix[i,j]=np.sqrt((points[i][0]-points[j][0])**2 + (points[i][1]-points[j][1])**2)
# 返回计算后的matrix return matrix # 进行初代矩阵生成 original_matrix = distance_matrix(points) # 检查初代矩阵 # print(original_matrix) # 蚁群算法类 class ACO: # 初始化(包括城市数目、距离矩阵、蚂蚁数目、迭代次数、信息素因子、距离因子、挥发因子、信息素强度) def __init__(self, num_cities, distance_matrix, num_ants, max_iter=200, alpha=2, beta=5, rho=0.5, q=100): # 城市数目 self.num_cities = num_cities # 距离矩阵 self.distance_matrix = distance_matrix # 信息素矩阵,其中shape属性返回数组的维度 self.pheromone = np.ones(self.distance_matrix.shape) / num_cities # 蚂蚁数目 self.num_ants = num_ants # 迭代次数 self.max_iter = max_iter # 信息素因子 self.alpha = alpha # 距离因子 self.beta = beta # 挥发因子 self.rho = rho # 信息素强度 self.q = q # 更新信息素(包括蚂蚁) def _update_pheromone(self, ants): # pheromone(t+1) = (1-rho)*pheromone(t) + ∑ delta[pheromone(t,t+1)] self.pheromone *= (1 - self.rho)
# 对于每一个蚂蚁,更新其放在边(i,i+1)上的信息素强度 for ant in ants: for i in range(self.num_cities-1): # delta[pheromone(t,t+1)] = Q / Li self.pheromone[ant[i]][ant[i+1]] += self.q / self.distance_matrix[ant[i]][ant[i+1]] # 更新最后一段路径的信息素 self.pheromone[ant[-1]][ant[0]] += self.q / self.distance_matrix[ant[-1]][ant[0]] # 根据信息素因子和距离因子,选择下一个需要访问的城市(包括当前的城市、已经访问的城市) def _choose_next_city(self, current_city, visited): # 可能性数组 probabilities = []
# 遍历所有城市 for i in range(self.num_cities): # 如果城市i没有被访问,则i可能是下一个选择的城市 if i not in visited: probabilities.append(self.pheromone[current_city][i] ** self.alpha * ((1.0 / self.distance_matrix[current_city][i]) ** self.beta)) # 如果城市i被访问 else: probabilities.append(0)
# 更新分母(需要除以sum) probabilities = probabilities / np.sum(probabilities) # 按照概率,轮盘抽取一个可能的城市i,作为下一个城市 return np.random.choice(range(self.num_cities), p=probabilities) # 解决TSP问题 def solve(self): # 初始化最好路线和距离 best_route = None best_distance = float('inf')
# 进行每一次的迭代 for _ in range(self.max_iter): # 初始化蚂蚁,令他们随机分配到一个城市 ants = [[np.random.randint(self.num_cities)] for _ in range(self.num_ants)]
# 遍历每一只蚂蚁 for ant in ants: # 生成完整的路径 for _ in range(self.num_cities-1): # 当前路径中的最后一个城市 current_city = ant[-1] # 调用函数,选择下一个访问的城市 next_city = self._choose_next_city(current_city, ant) # push到蚂蚁的数组里面 ant.append(next_city)
# 更新信息素 self._update_pheromone(ants)
# 遍历每一只蚂蚁 for ant in ants: # 生成距离 distance = sum([self.distance_matrix[ant[i]][ant[i + 1]] for i in range(-1, self.num_cities - 1)]) # 更新最好距离 if distance < best_distance: best_distance = distance best_route = ant
# 返回最优解 return best_route, best_distance # 蚂蚁的数量(城市数量的1.5倍) num_ants = int(num * 1.5) # 初始化aco类 aco = ACO(num, original_matrix, num_ants) # 利用类中的solve函数,进行TSP问题的求解 best_route, best_distance = aco.solve() # 结束计时 end = time.time() # 计算算法的耗时 during = end - start print(f"Time consumption: {during}s") # 输出最佳路线和距离 print(f"Best route: {best_route}") print(f"Best distance: {best_distance}") # 使用zip分离坐标 x, y =zip(*points) # 初始化新的x和y坐标的数组 newx = [] newy = [] # 根据best-route更新newx和newy for i in range(num): # 当前点的id是best-route中的编号 id = best_route[i] # 新增点的坐标信息 newx.append(x[id]) newy.append(y[id]) # 画出route图 plt.figure() plt.scatter(newx, newy, color='blue', s=2) for i in range(num): # 下一个点需要对num进行取余 next_i = (i + 1) % num plt.plot([newx[i], newx[next_i]], [newy[i], newy[next_i]], color='red') # 增加标签和标题 plt.xlabel("X-axis") plt.ylabel("Y-axis") plt.title("ACO algorithm for TSP problems") # 背景含网格 plt.grid(True) # 展示图片 plt.show() |
![P1025 [NOIP2001 提高组] 数的划分](https://img-blog.csdnimg.cn/direct/a0d5f18eb6a84e9fa3667dded9da1075.png)








![navigator.clipboard is undefined in JavaScript issue [Fixed]](https://img-blog.csdnimg.cn/direct/ba5792b02780438988eb14aa11d2788d.png)