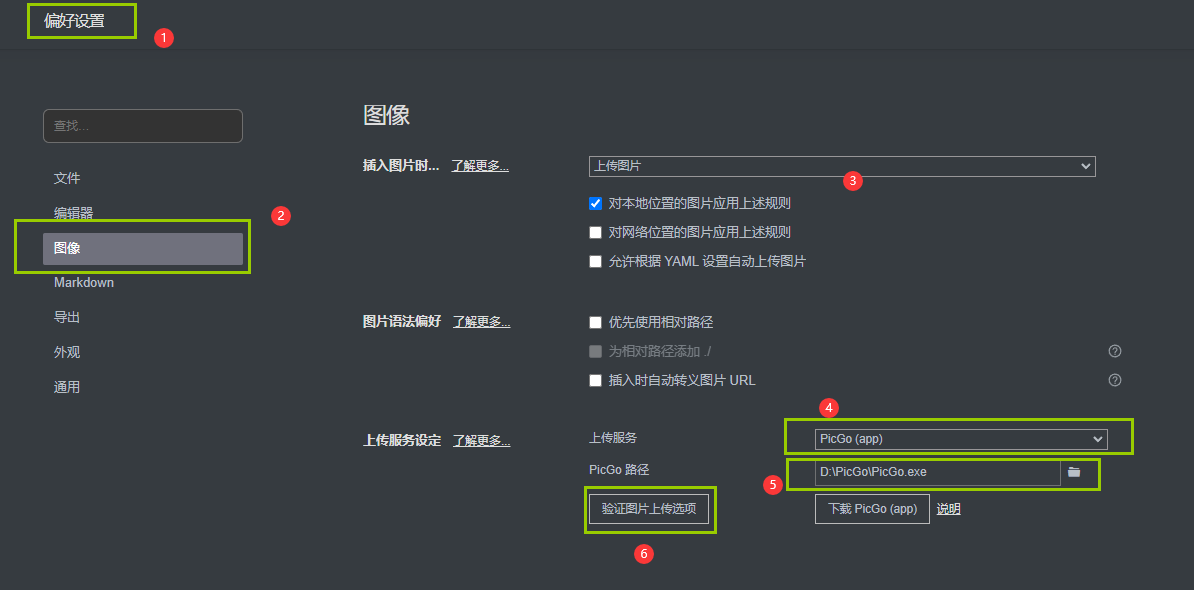
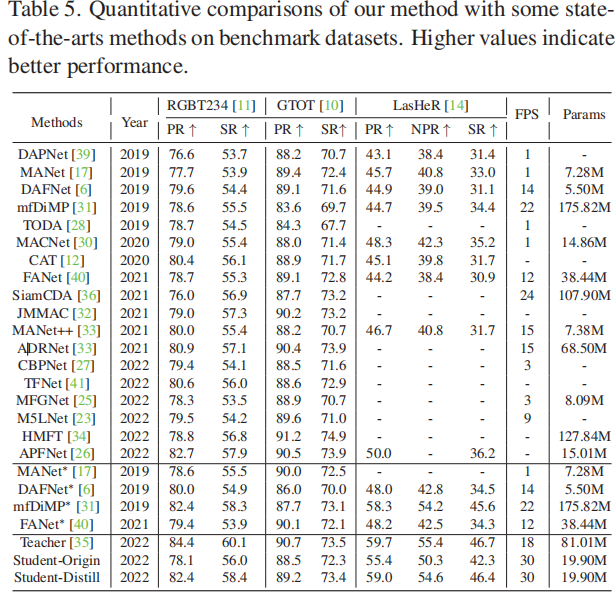
二分法:顾名思义,把问题一分为2的处理,是一种常见的搜索算法,用于在有序数组或这有序列表中查找指定元素的位置,它的思想是将待搜索的区间不断二分,然后比较目标值与中间元素的大小关系,然后确定下一步的搜索的方向
以下是二分法的基本步骤:
确定搜索区间的起始位置 left 和结束位置 right,通常初始时 left 为数组的第一个元素的索引,right 为数组的最后一个元素的索引。
在每一次循环中,计算中间位置 mid,即 mid = (left + right) / 2。
比较目标值与中间元素的大小关系:
如果目标值等于中间元素,则找到了目标值,返回中间元素的索引。
如果目标值小于中间元素,则目标值可能在左半部分,更新 right = mid - 1。
如果目标值大于中间元素,则目标值可能在右半部分,更新 left = mid + 1。
重复步骤 2-3,直到找到目标值或搜索区间为空(即 left > right)。
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
思路
标签:二分查找
过程:
设定左右指针
找出中间位置,并判断该位置值是否等于 target
nums[mid] == target 则返回该位置下标
nums[mid] > target 则右侧指针移到中间
nums[mid] < target 则左侧指针移到中间
时间复杂度:O(logN)
c++代码实现
class Solution {
public:
int search(vector<int>& nums, int target) {
int left=0;
int right=nums.size()-1;
while(left<=right){
int mid=left+(right-left)/2;
if(nums[mid]==target){
return mid;
}
else if(nums[mid]<target){
left=mid+1;
}
else
right=mid-1;
}
return -1;
}
};c语言写法
int search(int* nums, int numsSize, int target) { int left=0; int right=numsSize-1; while(left<=right){ int mid=left+(right-left)/2; if(nums[mid]<target){ left=mid+1; } else if(nums[mid]>target){ right=mid-1; } else return mid; } return -1; }
用递归来做
int binarySearchRecursive(int* nums, int left, int right, int target) {
if (left > right) {
return -1; // 搜索区间为空,未找到目标值
}
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
return mid; // 找到目标值,返回索引
} else if (nums[mid] < target) {
return binarySearchRecursive(nums, mid + 1, right, target); // 目标值可能在右半部分
} else {
return binarySearchRecursive(nums, left, mid - 1, target); // 目标值可能在左半部分
}
}