详解桶排序以及排序内容大总结
文章目录
- 详解桶排序以及排序内容大总结
- 堆
- 堆的操作(大)
- heapinsert --- 调整成大根堆
- heapify --- 移除原根节点后,继续调整成大根堆
- 堆中某个位置的数值发生改变
- 堆排序
- 优化
- 堆练习
- 比较器
- 桶排序
- 基数排序
堆
注:堆是一种特殊的二叉树
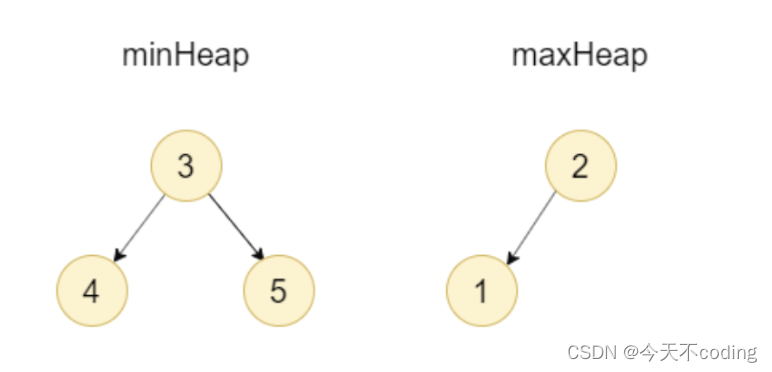
堆分为大根堆(以某一节点为根节点的整棵树中最大值为该节点)和小根堆(以某一节点为根节点的整棵树中最小值为该节点)
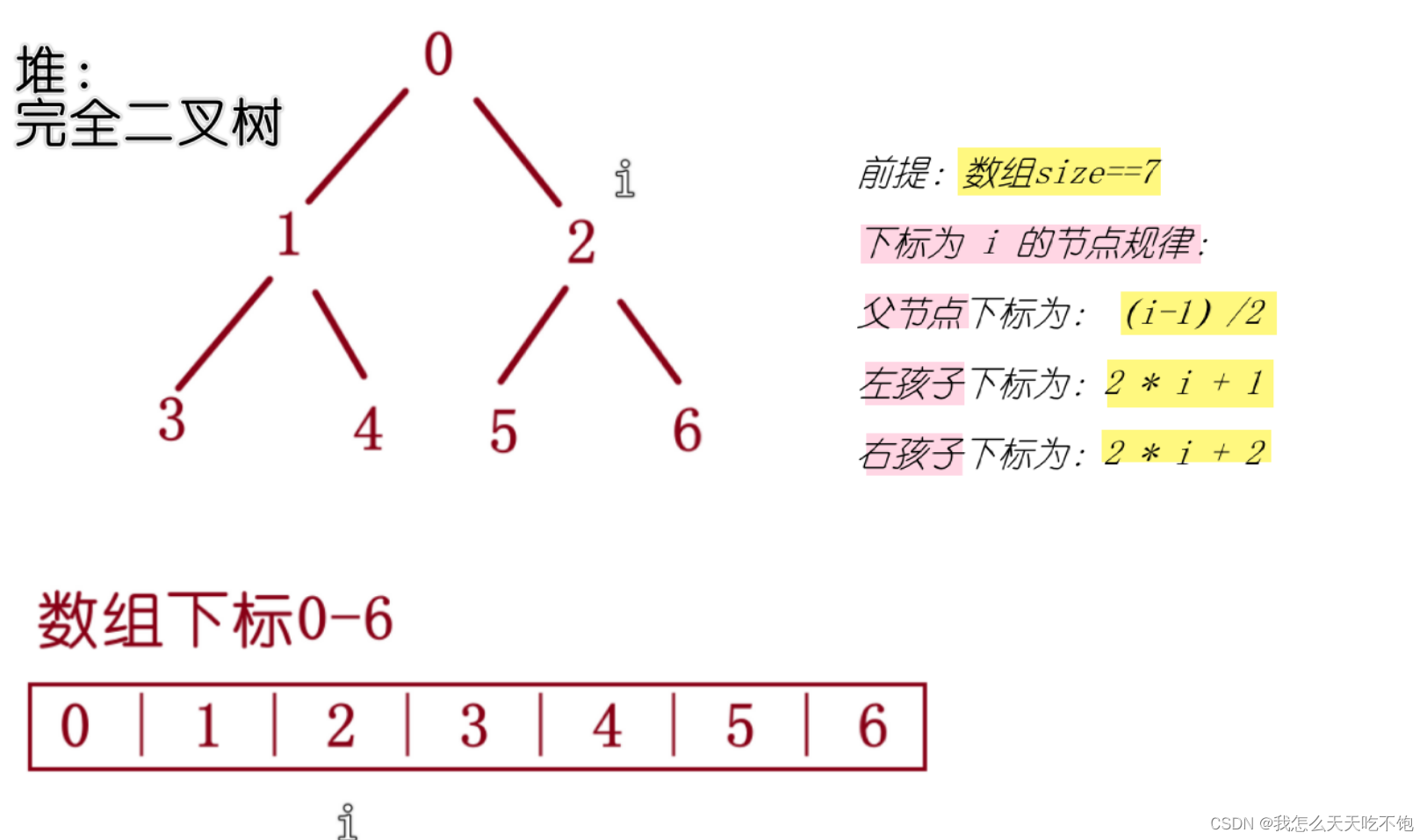
堆的操作(大)
heapinsert — 调整成大根堆
假设一个用户不断地给出数,程序拿到数字并将在此之前的所有数字调整成大根堆
- 找父节点
(i-1)/2进行比较,比父节点大则交换位置
代码实现:
/**
* 调整过程:某个数正处在index的位置,不断往上调整位置时
*
* 新节点比自己的父节点大,位置需要置换
* 置换以后新节点处于父节点位置,下标需要改变
* @param arr
* @param index
*/
public static void heapInsert(int[]arr,int index){
//while停止条件:
//1:来到了一个合适的位置,比自己的父亲节点小,不需要再调整
//2:来到了根节点,根节点下标为0,(0-1)/2==0,自己不会比自己大,while停止
while(arr[index] > arr[(index-1)/2]){
//置换
swap(arr,index,(index-1)/2);
//改变该节点位置
index = (index-1)/2;
}
}
heapify — 移除原根节点后,继续调整成大根堆
假设用户停止抛出数字,让程序返回在此之前的所有数中的最大值,并且将剩下的数再次调整成为大根堆
- 返回下标为0的数字,即为最大值
- 将堆中的最后一个数的位置调换到根节点的位置(用root标记),数组长度-1,开始调整
- 调整步骤:在root节点的左孩子和右孩子之中选择一个最大值,与root进行比较,root比较小的话则调换位置;继续上述调整步骤,知道root节点比自己的左右孩子都大,或者没有左右孩子时
代码实现:
/**
* 剔除最大值后,对剩下的节点调整成大根队
* @param arr
* @param index 初始index 可以从任何一个位置往下调整
* @param heapSize 堆的大小
*/
public static void heapIfy(int[] arr,int index,int heapSize){
//左孩子下标
int left = index*2+1;
//左孩子下标还没有越界,证明还有孩子
while(left<heapSize){
//左右孩子PK
int largest = left +1 <heapSize && arr[left+1]>arr[left]?
left+1: //如果右孩子的下标没有越界 且 右孩子比左孩子大
left; //反之,右孩子越界或左孩子比较大则都选左孩子
//父节点和较大的孩子节点PK
if (arr[largest] > arr[index]){ //孩子节点比较大
//孩子节点与父节点交换
swap(arr,largest,index);
index = largest; //此时的父节点处在孩子节点的位置
left = index *2 +1; //此时的父节点的左孩子位置
//继续循环换位置
}else { //孩子节点没有比父节点大,大根堆形成
break;
}
}
}
堆中某个位置的数值发生改变
- 变大:往上进行heapInsert
- 变小:往下惊醒heapIfy
堆排序
- 调整成大根堆,剔除最大值(根节点),将最后一个位置上的数放到根节点上,heapSize–
- 继续调整,剔除,更新位置,heapSize
- 直到排序完成
代码实现:
/**
* 堆排序代码实现
* @param arr
*/
public static void heapSort(int[] arr){
//arr为空或arr只有一个或零个数
if(arr==null || arr.length<2){
return;
}
//初始大根堆
for (int i = 0;i<arr.length;i++){ //O(N)
heapInsert(arr,i); //O(log N)
}
int heapSize = arr.length; //初始大根堆长度
swap(arr,0,-heapSize); //0位置上堆中最后的位置做交换
//当堆的长度不为0时,需要不断拿走根节点,再重新调整
while (heapSize > 0){ //O(N)
heapIfy(arr,0,heapSize); //O(log N)
swap(arr,0,--heapSize);
}
}
优化
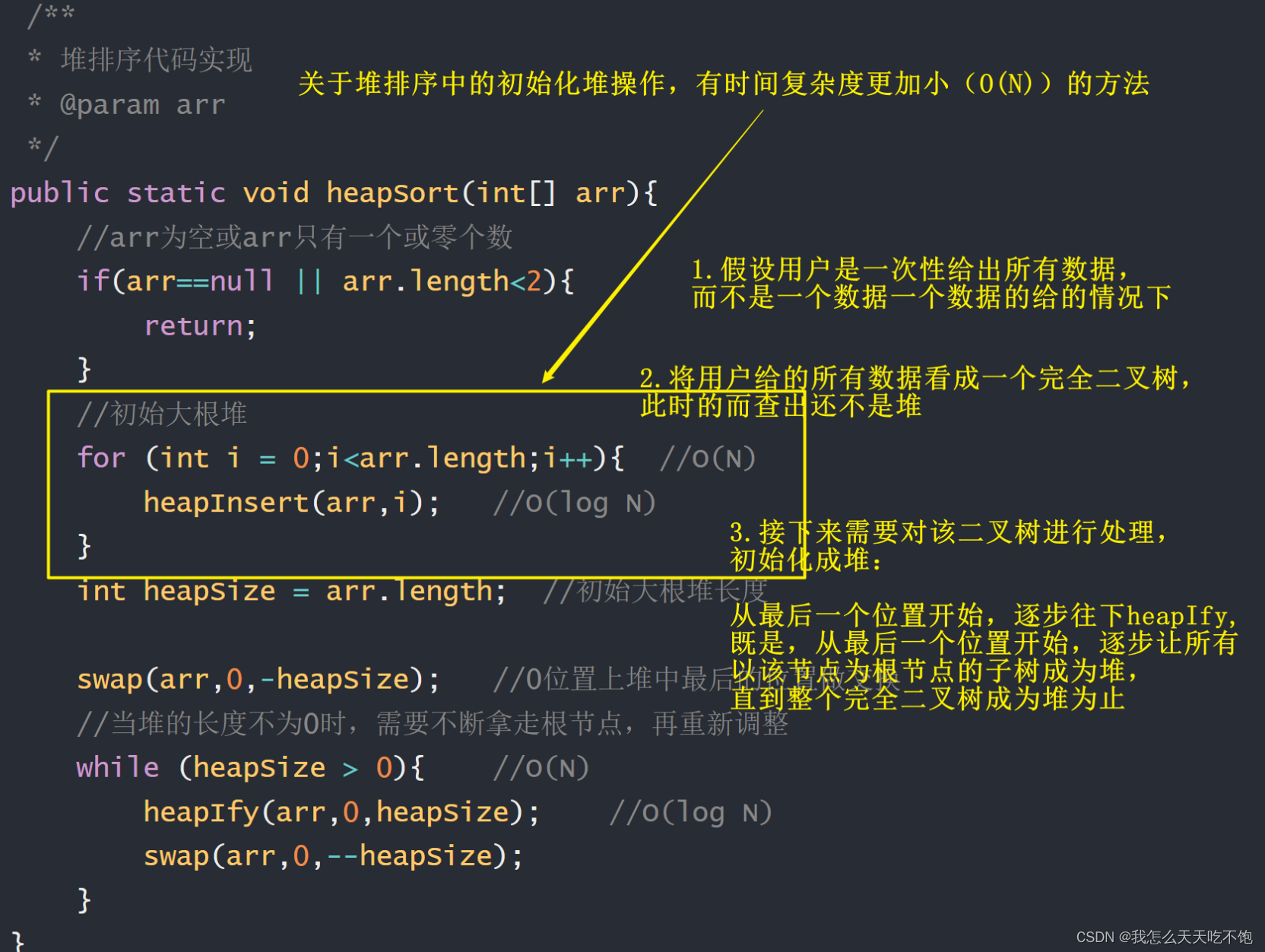
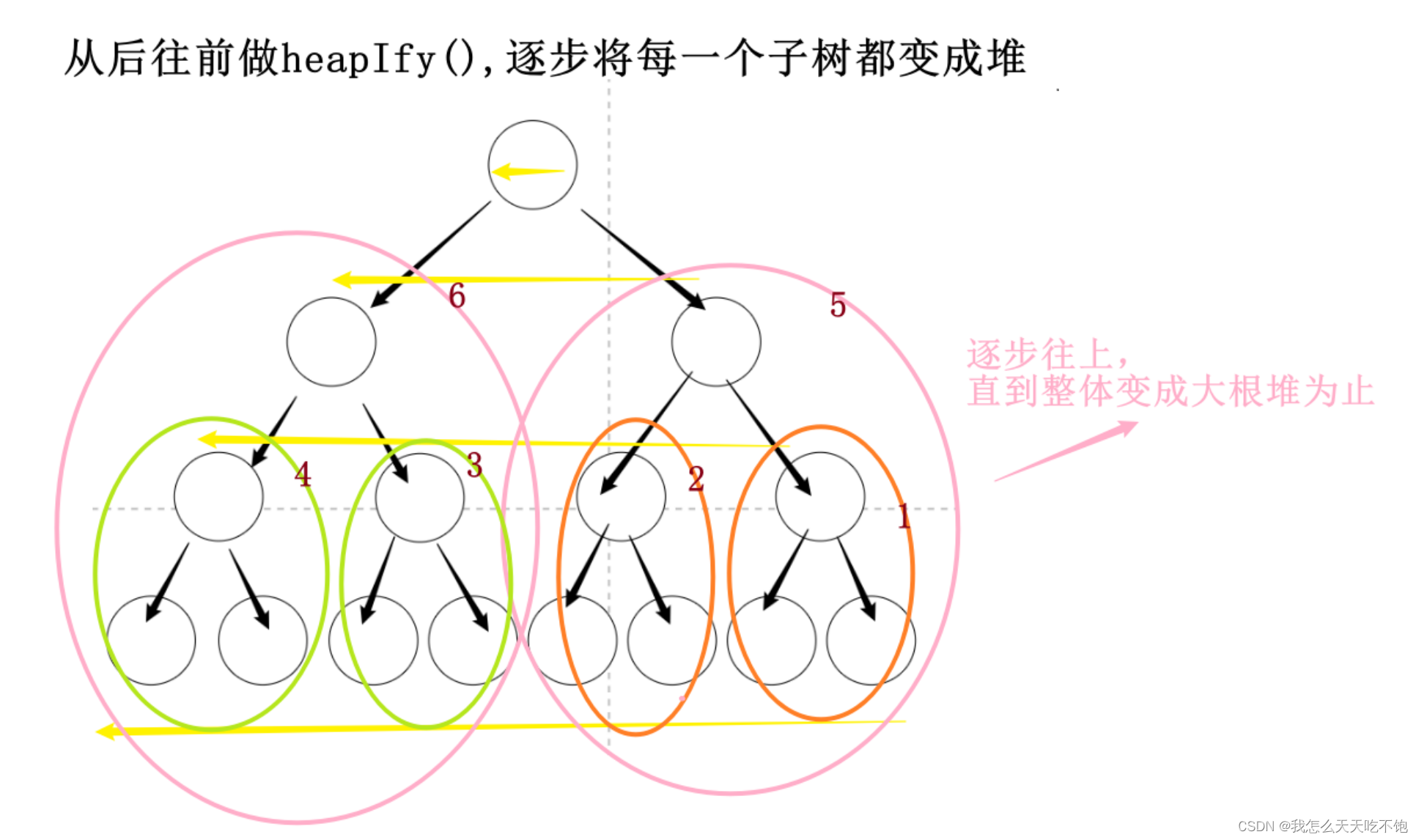
完全二叉树的叶子节点:
- 如果是偶数个节点,叶子节点等于总节点除以2, 即 N % 2==0, n = N/2
- 如果是奇数个节点,叶子节点等于==(总节点+1)除以2==, 即 N % 2 == 1, n = (N+1)/2
时间复杂度:假设数组中有N个数,叶子节点为N/2个叶子节点
- 最底层的叶子节点的时间复杂度即为:
(N/2)*1(1为只进行一次操作,因为叶子节点没有子节点,只遍历) - 倒数第二层的节点的时间复杂度:
(N/4)*2(2为 遍历+往下移动一层) - 倒数第三层的节点的时间复杂度:
(N/8)*3(3为 遍历+往下移动2层) - 以此类推
T ( N ) = N / 2 ∗ 1 + N / 4 ∗ 2 + N / 8 ∗ 3 + . . . + 1 ∗ l o g 2 N T(N)=N/2*1+N/4*2+N/8*3+...+1*log2 N T(N)=N/2∗1+N/4∗2+N/8∗3+...+1∗log2N
错位相减2T(N)-T(N)==T(N) 结果为O(N)
代码实现:
//更快的初始化堆的方法 时间复杂度O(N)
for (int i = arr.length-1;i>=0;i--){
heapIfy(arr,i, arr.length);
}
堆练习
堆排序扩展题目
已知一个几乎有序的数组,几乎有序是指,如果把数组排好顺序的话,每个元素移动的距离可以不超过k,并且k相对于数组来说比较小。请选择一个合适的排序算法针对这个数据进行排序。
题解:
每一个元素移动的距离都不超过K:意味着,在数组的 0~K 的范围内的最小值即为整个数组的最小值,K+1位置以后的数也全都不可能移动到 0 位置上。
所以,只需要 使用一个固定长度为 K+1的滑动窗口或双指针,不断的选出该范围内的最小值,然后不断地推后该滑动窗口。
Java中现成的堆结构:优先级队列:
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();默认小根堆,想要大根堆则传入比较器指定比较挥着
底层是数组:
扩容机制???
默认堆结构,只支持用户给出一个数,和系统弹出最值并移除(黑盒)
比较器
public static class myCompare implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;
}
}
桶排序
之前所有的排序都是只和两个数之间的比较有关系。(基于比较的排序)
不基于比较的排序(根据数据状况定制):
例子:员工年龄排序,返回0-200
解题思路:申请一个长度为200的数组,下标 i 认为是年龄,i 位置的值为年龄为 i 的人数。
时间复杂度:O(N)
不基于比较的排序都是根据数据状况做的排序,应用范围比基于比较的排序小。
基数排序