数据流的中位数

问题描述

中位数是有序整数列表中的中间值。如果列表的大小是偶数，则没有中间值，中位数是两个中间值的平均值。

例如 arr = [2,3,4] 的中位数是 3 。
例如 arr = [2,3] 的中位数是 (2 + 3) / 2 = 2.5 。
实现 MedianFinder 类:

MedianFinder() 初始化 MedianFinder 对象。

void addNum(int num) 将数据流中的整数 num 添加到数据结构中。

double findMedian() 返回到目前为止所有元素的中位数。与实际答案相差 10-5 以内的答案将被接受。

详见leetcode295

问题分析

查大用小，查小用大，查中间则需要两个堆，一个最大堆，一个最小堆，遍历元素，当最小堆为空或者当前元素大于最小堆堆顶元素时，放入最小堆，否则放入最大堆，当两个堆的元素数量相差大于1时，数量多的堆移除堆顶元素，放入另一个堆。如此，遍历结束后，小顶堆中存放着全部元素中较大的一半，大顶堆中存储着全部元素中较小的一半。中位数或为两个堆顶元素的均值，或者为数量多的堆的堆顶元素

图示过程

以添加[1,2,3,4,5]为例，展示两个堆的变化过程，初始时，两个堆均为空。
1.添加1，此时minHeap为空，添加到minHeap中

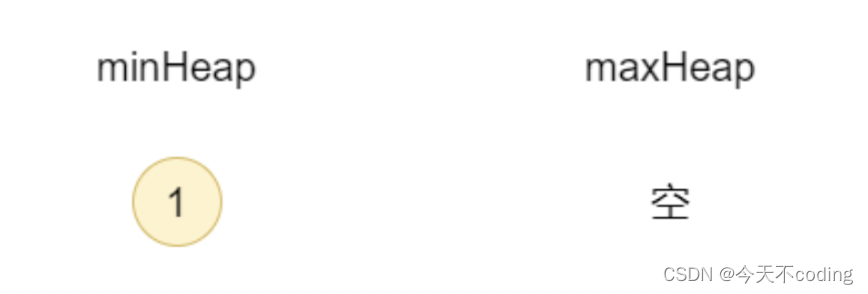
2.添加2,2>minHeap的堆顶元素1，添加到minHeap中，此时minHeap中的元素数量为2，maxHeap中的元素数量为0,数量差大于1，所以minHeap移除堆顶元素，放入maxHeap中

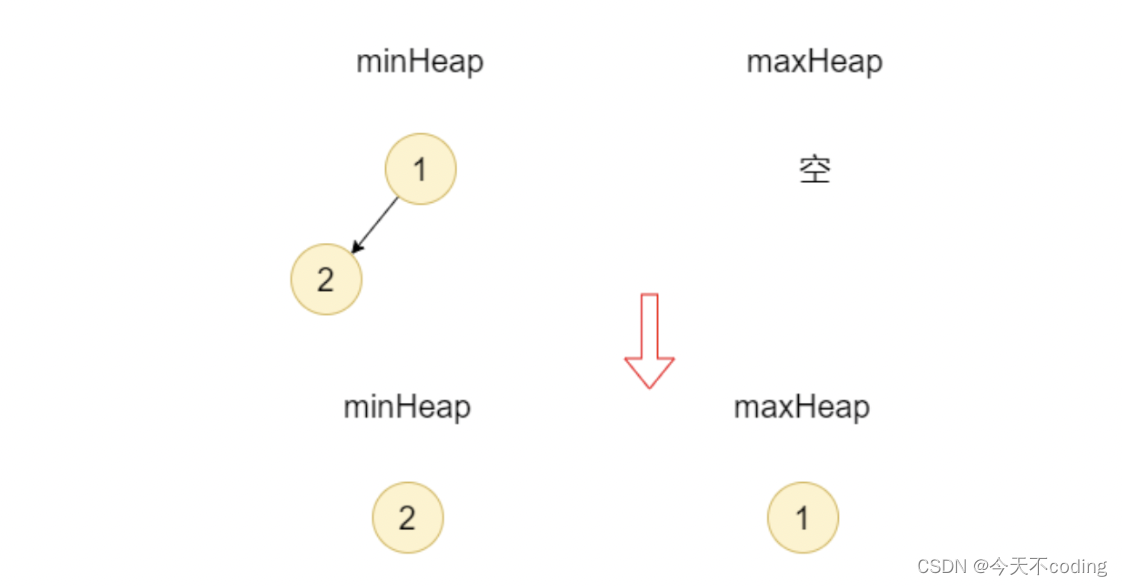
3.添加3，3>minHeap的堆顶元素2，添加到minHeap中，此时minHeap中的元素数量为2，maxHeap中的元素数量为1,数量差等于1，无需再操作

4.添加4，4>minHeap的堆顶元素2，添加到minHeap中，此时minHeap中的元素数量为3，maxHeap中的元素数量为1,数量差大于1，所以minHeap移除堆顶元素，放入maxHeap中

5.添加5，5>minHeap的堆顶元素3，添加到minHeap中，此时minHeap中的元素数量为3，maxHeap中的元素数量为2,数量差等于1，无需再操作

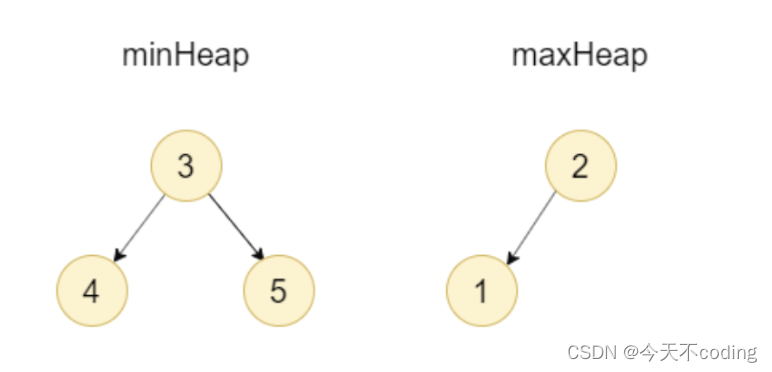
此时，两个堆的元素数量相差1，中位数为两个堆的堆顶元素均值

代码实现

class MedianFinder {
    PriorityQueue<Integer> minHeap;
    PriorityQueue<Integer> maxHeap;

    public MedianFinder() {
        minHeap = new PriorityQueue<Integer>((a, b) -> a - b);
        maxHeap = new PriorityQueue<Integer>((a, b) -> b - a);
    }
    
    public void addNum(int num) {
        if (minHeap.isEmpty() || num > minHeap.peek()) {
            minHeap.offer(num);
            if (minHeap.size() - maxHeap.size() > 1) {
                maxHeap.offer(minHeap.poll());
            }
        } else {
            maxHeap.offer(num);
            if (maxHeap.size() - minHeap.size() > 1) {
                minHeap.offer(maxHeap.poll());
            }
        }
    }
    
    public double findMedian() {
        if (minHeap.size() == maxHeap.size()) {
            return (minHeap.peek() + maxHeap.peek()) / 2.0;
        }else{
            return minHeap.size()>maxHeap.size()? minHeap.peek() : maxHeap.peek();
        }
    }
}