---

前言

机器学习中往往通过度量来研究不同样本或数据集之间的差异性，合适的度量方式可以显著提高算法的准确率，因此在接下来的内容中介绍博主目前常用的距离度量方法。

一、前期准备

为了方便理解，先设置两个二维平面上的点a(x1,y1)，点b(x2,y2)，下列所有的距离度量都默认使用点a和点b，距离都用d表示，不再赘述。

二、距离度量方法

1. 欧氏距离

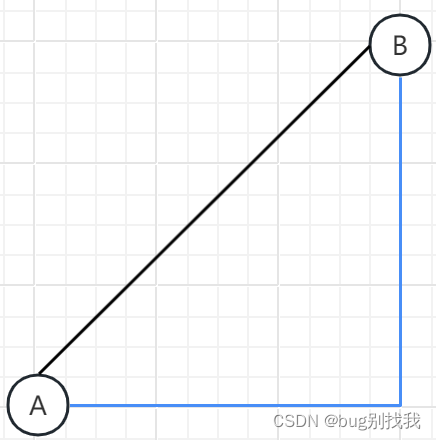
欧氏距离起源于勾股定理，全称为欧几里得距离；它代表两点之间的直线距离，如下图所示，A,B点之间的蓝色线条就代表它的欧氏距离。

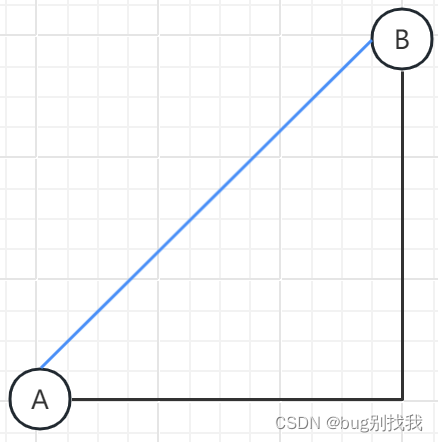
计算公式如下

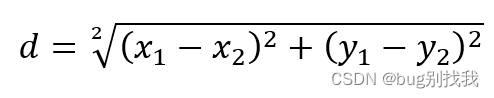
2.曼哈顿距离

曼哈顿距离的名称来源于美国纽约曼哈顿区的街道规划。在曼哈顿，街道规划呈矩形网格状，使得行人和车辆只能沿着网格线移动，而不能直线穿越街区。如下图所示，意为坐标系上轴坐标距离的差值的和。

计算公式如下

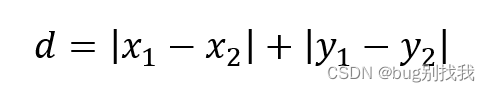
3.切比雪夫距离

切比雪夫距离得名自俄罗斯数学家切比雪夫。
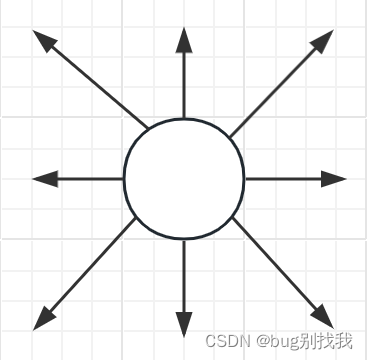
使用切比雪夫距离计算两点之间的距离时，平面上的点向八个方向移动的距离或者说代价是一样的（如下图所示，画的有点丑，见谅见谅）；如果有玩过国际象棋的朋友可以试试联想王的移动方式；因此计算切比雪夫距离只需要最大的轴坐标之差。

计算公式如下

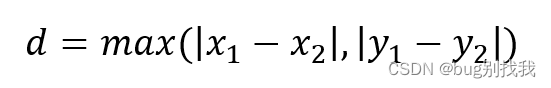
4. 闵可夫斯基距离

闵科夫斯基距离实际上是欧式距离、曼哈顿距离、切比雪夫距离在笛卡尔坐标系下的一种推广，或者将它们统合在一个框架下。
计算公式如下

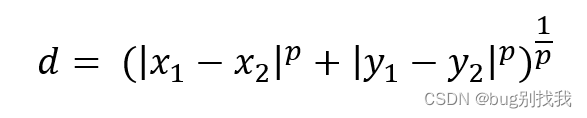
当p=1的时候，1阶闵科夫斯基距离等价于曼哈度距离；
当p=2的时候，2阶闵科夫斯基距离等价于欧几里得距离；
当p=∞的时候，∞阶闵科夫斯基距离等价于切比雪夫距离。

总结

目前只统计了博主自己遇到的一些度量方法，其余方法后期会慢慢补充。