分类目录：《深入理解强化学习》总目录

在本文中，我们将介绍备份（Backup）的概念。备份类似于自举之间的迭代关系，对于某一个状态，它的当前价值是与它的未来价值线性相关的。 我们将与下图类似的图称为备份图（Backup Diagram）或回溯图，因为它们所示的关系构成了更新或备份操作的基础，而这些操作是强化学习方法的核心。这些操作将价值信息从一个状态（或状态—动作对）的后继状态（或状态—动作对）转移回它。 每一个空心圆圈代表一个状态，每一个实心圆圈代表一个状态-动作对。

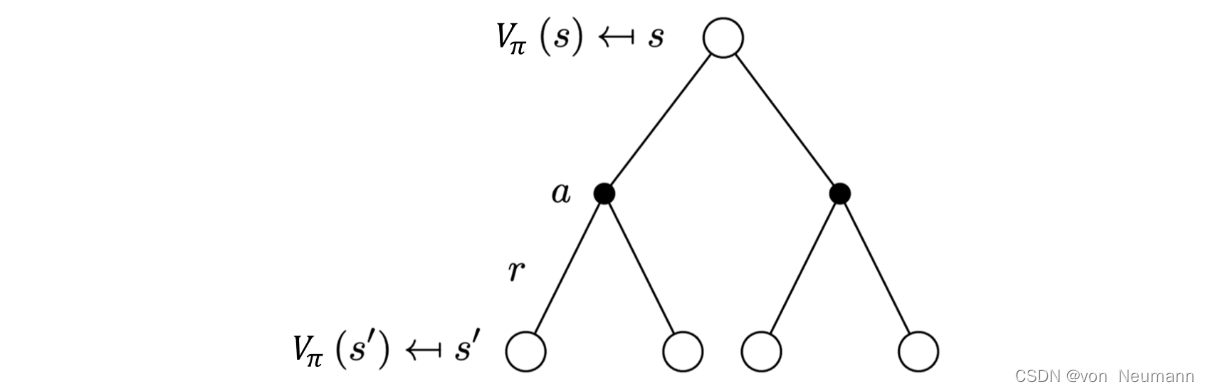
如下式所示，这里有两层加和。第一层加和是对叶子节点进行加和，往上备份一层，我们就可以把未来的价值（$s^{\prime }$的价值）备份到黑色的节点。 第二层加和是对动作进行加和，得到黑色节点的价值后，再往上备份一层，就会得到根节点的价值，即当前状态的价值。
$$V_{\pi }(s)=\sum _{a\in A}\pi (a|s)(R(s,a)+\gamma \sum _{s^{\prime }\in S}p(s^{\prime }|s,a)V_{\pi }(s^{\prime }))$$

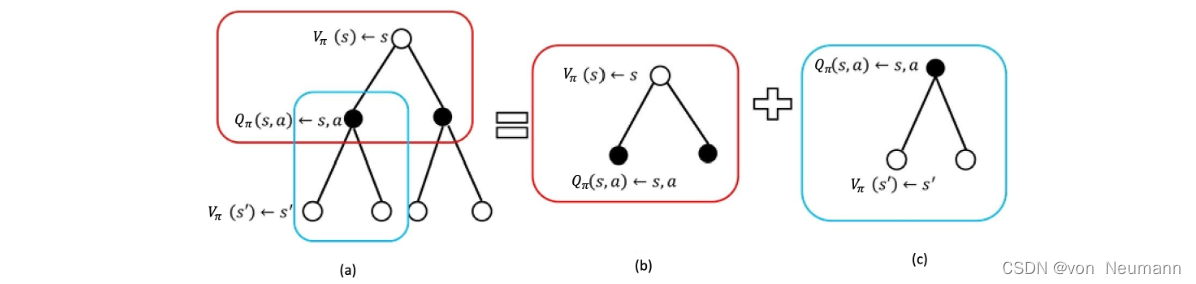
下图所示为状态价值函数的计算分解，其中子图($b$)的计算公式为：
$$V_{\pi }(s)=\sum _{a\in A}\pi (a|s)Q_{\pi }(s,a)$$

其给出了状态价值函数与Q函数之间的关系。子图($c$)计算Q函数为：
$$Q_{\pi }(s,a)=R(s,a)+\gamma \sum _{s^{\prime }\in S}p(s^{\prime }|s,a)V_{\pi }(s^{\prime })$$

我们将上两式的$Q_{\pi }(s,a)$替换可得：
$$V_{\pi }(s)=\sum _{a\in A}\pi (a|s)(R(s,a)+\gamma \sum _{s^{\prime }\in S}p(s^{\prime }|s,a)V_{\pi }(s^{\prime }))$$

所以备份图给出了未来下一时刻的状态价值函数与上一时刻的状态价值函数之间的关联：

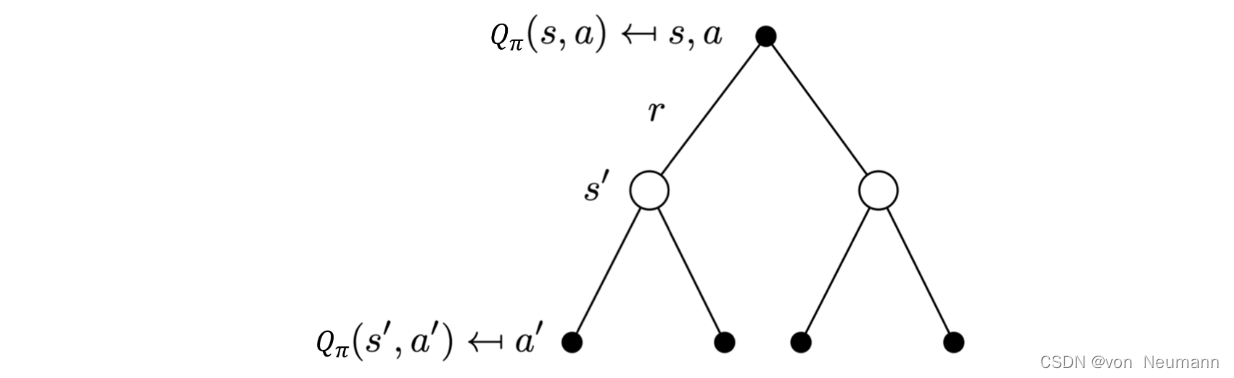
对于Q函数，我们也可以进行这样的一个推导。如下图所示，现在的根节点是Q函数的一个节点。Q函数对应于黑色的节点。下一时刻的Q函数对应于叶子节点，有4个黑色的叶子节点：
$$Q_{\pi }(s,a)=R(s,a)+\gamma \sum _{s^{\prime }\in S}p(s^{\prime }|s,a)\sum _{a^{\prime }\in A}\pi (a^{\prime }|s^{\prime })Q_{\pi }(s^{\prime },a^{\prime })$$

如上式所示，这里也有两层加和。第一层加和先把叶子节点从黑色节点推到空心圆圈节点，进入到空心圆圈结点的状态。 当我们到达某一个状态后，再对空心圆圈节点进行加和，这样就把空心圆圈节点重新推回到当前时刻的Q函数。

下图子图($c$)中：
$$V_{\pi }(s^{\prime })=\sum _{a^{\prime }\in A}\pi (a^{\prime }|s^{\prime })Q_{\pi }(s^{\prime },a^{\prime })$$

我们将上式代入上文中$Q_{\pi }(s,a)$算式可得未来Q函数与当前Q函数之间的关联，即：
$$Q_{\pi }(s,a)=R(s,a)+\gamma \sum _{s^{\prime }\in S}p(s^{\prime }|s,a)\sum _{a^{\prime }\in A}\pi (a^{\prime }|s^{\prime })Q_{\pi }(s^{\prime },a^{\prime })$$

参考文献：
[1] 张伟楠, 沈键, 俞勇. 动手学强化学习[M]. 人民邮电出版社, 2022.
[2] Richard S. Sutton, Andrew G. Barto. 强化学习（第2版）[M]. 电子工业出版社, 2019
[3] Maxim Lapan. 深度强化学习实践（原书第2版）[M]. 北京华章图文信息有限公司, 2021
[4] 王琦, 杨毅远, 江季. Easy RL：强化学习教程 [M]. 人民邮电出版社, 2022