在上篇文章中，我们说利用堆的插入和删除也可以排序数据，但排序的只是堆里面的数组；同时每次排序数据都要单独写一个堆的实现，很不方便，这次就来着重讲讲如何使用堆排序。

1.建堆

给了你数据，要利用堆对数据进行排序，首先得将数据变成一个堆吧；那么如何将一串数据在逻辑结构上变成堆？

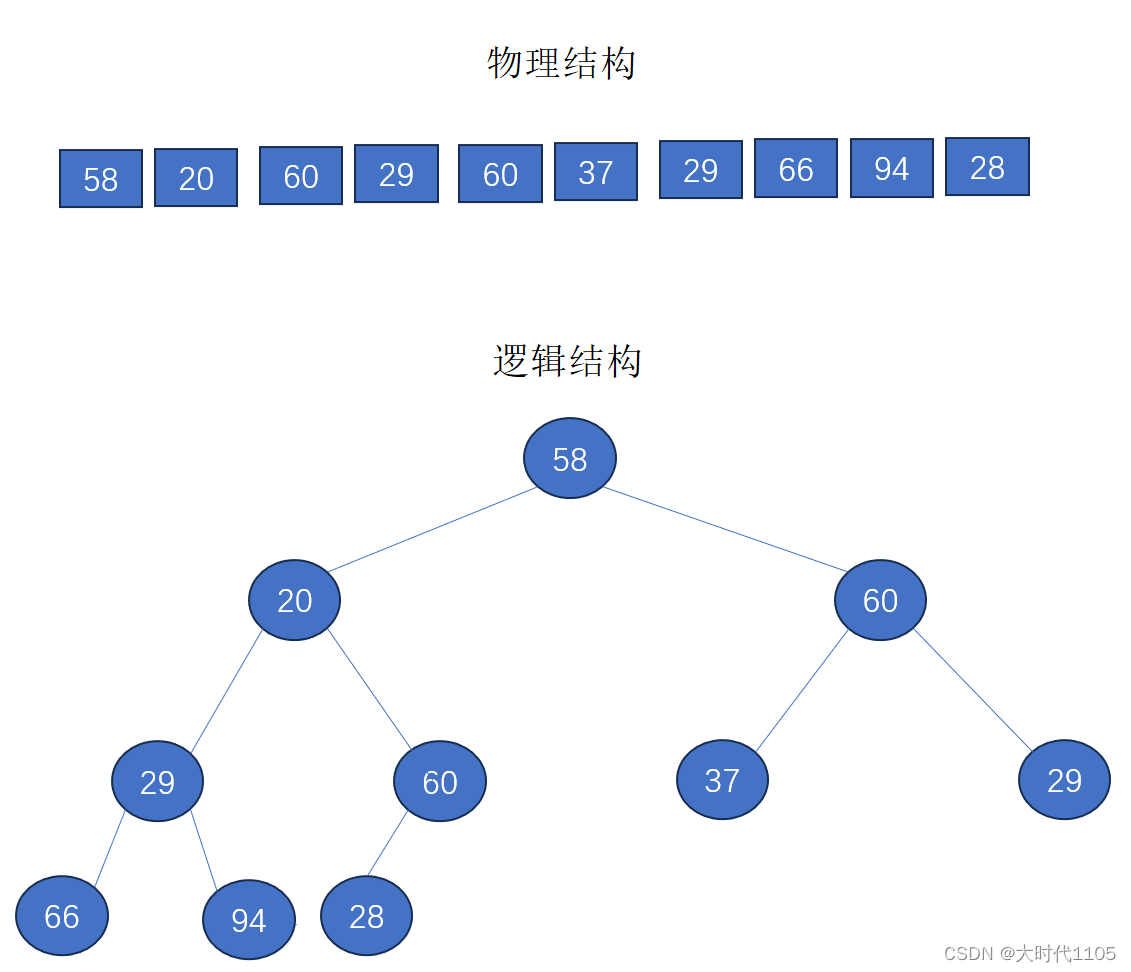要建堆，我们得先确定是建小堆，还是建大堆？这里我们先给出结论：升序建大堆，降序建小堆；为什么是这样？后面会进一步解释

我们就排升序，降序是同理的；要建大堆，有两种方法：

1. 向上调整：可以借鉴堆插入数据时的思想，每插入一个数据就对堆尾的数据执行一次向上调整算法；我们可以模拟数据进堆的过程，即先对第一个数据向上调整，再对第二个数据向上调整......直到最后一个数据

   //建堆方法1：向上调整
   for (int i = 0; i < size; i++)
   {
       AdjustUp(a, i);
   }

2. 向下调整：怎么让数据的逻辑结构变成堆？只要保证每个子树都是一个堆，那整个树就是一个堆；因此，我们从最后一个结点的父结点开始，从右到左，从下往上，依次对除了叶结点以外的结点使用向下调整算法

   //建堆方法2：向下调整
   for (int i = (size - 1 - 1) / 2; i >= 0; i--)
   {
       AdjustDown(a, size, i);
   }

至于向上调整算法和向下调整算法的实现，在上篇文章已经细讲：详解二叉树-CSDN博客

2.排序

建好堆，接下来就是如何利用堆的性质进行排序；这里我们同样可以借鉴堆删除数据时的思想，堆顶的数据是最大值，将堆顶的数据和堆尾的数据交换，是不是就将最大的数据排序好了(要排升序，最大的数据肯定是在堆尾)；这时，再对前size-1个数据中的堆顶数据向下调整，就筛选出了次大的数据，再跟堆尾数据交换......

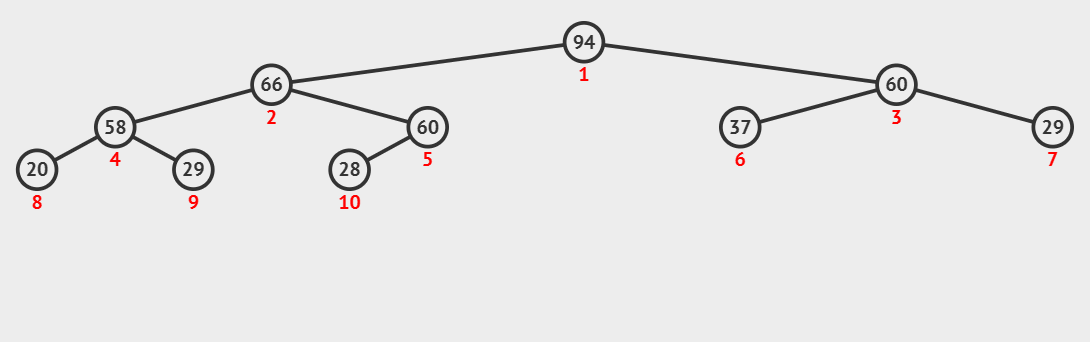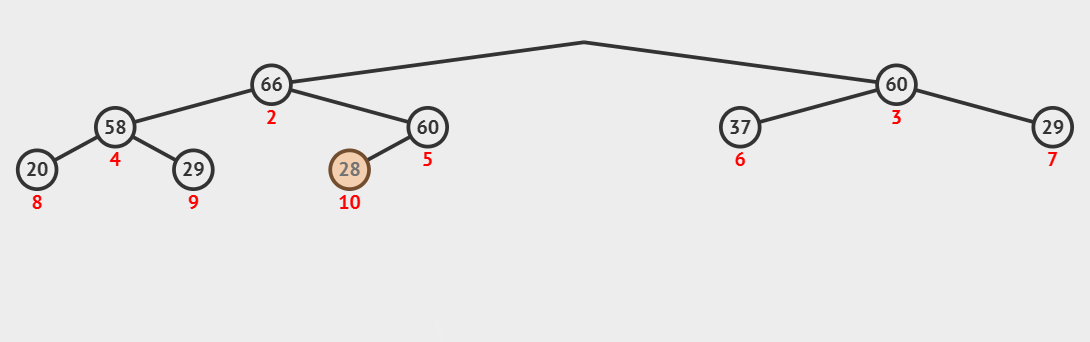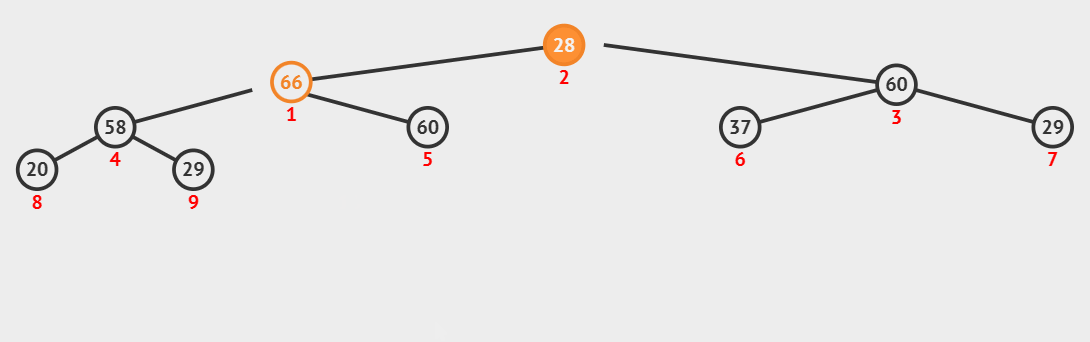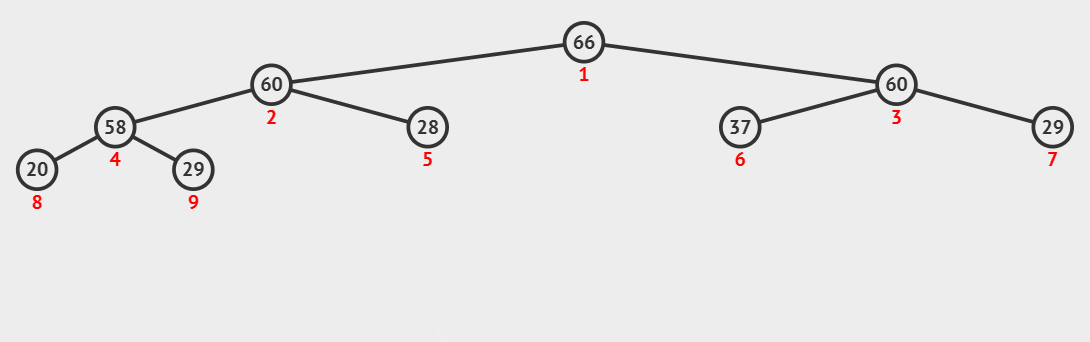
//排序
int end = size - 1;
while (end > 0)
{
    Swap(&a[0], &a[end]);
    AdjustDown(a, end, 0);
    end--;
}

这就是为什么升序要建大堆，因为我们需要将堆顶和堆尾数据交换；如果是小堆，把小的数据换到了后面，最后排成的是降序

在建堆过程中，推荐使用向下调整算法，理由如下：

1. 向下调整算法比向上调整算法效率高(下面会给出证明)

2. 我们发现排序过程也使用向下调整算法，两个部分可以一起用，不用花时间写向上调整算法了

3.算法的时间复杂度计算

3.1向上调整算法

因此，向上调整算法的时间复杂度是：

3.2向下调整算法

向下调整算法的时间复杂度：

3.3排序

排序过程中，交换堆顶和堆尾数据后，将堆顶数据向下调整，一共N个数

排序的时间复杂度：

---

堆排序的源码可以自行去我的Gitee主页获取HeapSort/HeapSort · baiyahua/LeetCode - 码云 - 开源中国 (gitee.com)