文章目录
- 14.3 US Baby Names 1880–2010(1880年至2010年美国婴儿姓名)
- 1 Analyzing Naming Trends(分析命名趋势)
- 评价命名多样性的增长
- “最后一个字母”的变革
- 变成女孩名字的男孩名字(以及相反的情况)
14.3 US Baby Names 1880–2010(1880年至2010年美国婴儿姓名)
这个数据是从1880年到2010年婴儿名字频率数据。我们先看一下这个数据长什么样子:
个数据集可以用来做很多事,例如:
- 计算指定名字的年度比例
- 计算某个名字的相对排名
- 计算各年度最流行的名字,以及增长或减少最快的名字
- 分析名字趋势:元音、辅音、长度、总体多样性、拼写变化、首尾字母等
- 分析外源性趋势:圣经中的名字、名人、人口结构变化等
之后的教程会涉及到其中一些。另外可以去官网直接下载姓名数据,Popular Baby Names。
下载National data之后,会得到names.zip文件,解压后,可以看到一系列类似于yob1880.txt这样名字的文件,说明这些文件是按年份记录的。这里使用Unix head命令查看一下文件的前10行:
!head -n 10 ../datasets/babynames/yob1880.txt
由于这是一个非常标准的以逗号隔开的格式(即CSV文件),所以可以用pandas.read_csv将其加载到DataFrame中:
import pandas as pd
# Make display smaller
pd.options.display.max_rows = 10
names1880 = pd.read_csv('../datasets/babynames/yob1880.txt', names=['names', 'sex', 'births'])
names1880
| names | sex | births | |
|---|---|---|---|
| 0 | Mary | F | 7065 |
| 1 | Anna | F | 2604 |
| 2 | Emma | F | 2003 |
| 3 | Elizabeth | F | 1939 |
| 4 | Minnie | F | 1746 |
| ... | ... | ... | ... |
| 1995 | Woodie | M | 5 |
| 1996 | Worthy | M | 5 |
| 1997 | Wright | M | 5 |
| 1998 | York | M | 5 |
| 1999 | Zachariah | M | 5 |
2000 rows × 3 columns
这些文件中仅含有当年出现超过5次以上的名字。为了简单化,我们可以用births列的sex分组小计,表示该年度的births总计:
names1880.groupby('sex').births.sum()
sex
F 90993
M 110493
Name: births, dtype: int64
由于该数据集按年度被分割成了多个文件,所以第一件事情就是要将所有数据都组装到一个DataFrame里面,并加上一个year字段。使用pandas.concat可以做到:
# 2010是最后一个有效统计年度
years = range(1880, 2011)
pieces = []
columns = ['name', 'sex', 'births']
for year in years:
path = '../datasets/babynames/yob%d.txt' % year
frame = pd.read_csv(path, names=columns)
frame['year'] = year
pieces.append(frame)
# 将所有数据整合到单个DataFrame中
names = pd.concat(pieces, ignore_index=True)
这里要注意几件事。
- 第一,
concat默认是按行将多个DataFrame组合到一起的; - 第二,必须指定
ignore_index=True,因为我们不希望保留read_csv所返回的原始索引。
现在我们得到了一个非常大的DataFrame,它含有全部的名字数据。现在names这个DataFrame看上去是:
names
| name | sex | births | year | |
|---|---|---|---|---|
| 0 | Mary | F | 7065 | 1880 |
| 1 | Anna | F | 2604 | 1880 |
| 2 | Emma | F | 2003 | 1880 |
| 3 | Elizabeth | F | 1939 | 1880 |
| 4 | Minnie | F | 1746 | 1880 |
| ... | ... | ... | ... | ... |
| 1690779 | Zymaire | M | 5 | 2010 |
| 1690780 | Zyonne | M | 5 | 2010 |
| 1690781 | Zyquarius | M | 5 | 2010 |
| 1690782 | Zyran | M | 5 | 2010 |
| 1690783 | Zzyzx | M | 5 | 2010 |
1690784 rows × 4 columns
有了这些数据后,我们就可以利用groupby或pivot_table在year和sex界别上对其进行聚合了:
total_births = names.pivot_table('births', index='year',
columns='sex', aggfunc=sum)
total_births.tail()
| sex | F | M |
|---|---|---|
| year | ||
| 2006 | 1896468 | 2050234 |
| 2007 | 1916888 | 2069242 |
| 2008 | 1883645 | 2032310 |
| 2009 | 1827643 | 1973359 |
| 2010 | 1759010 | 1898382 |
import seaborn as sns
%matplotlib inline
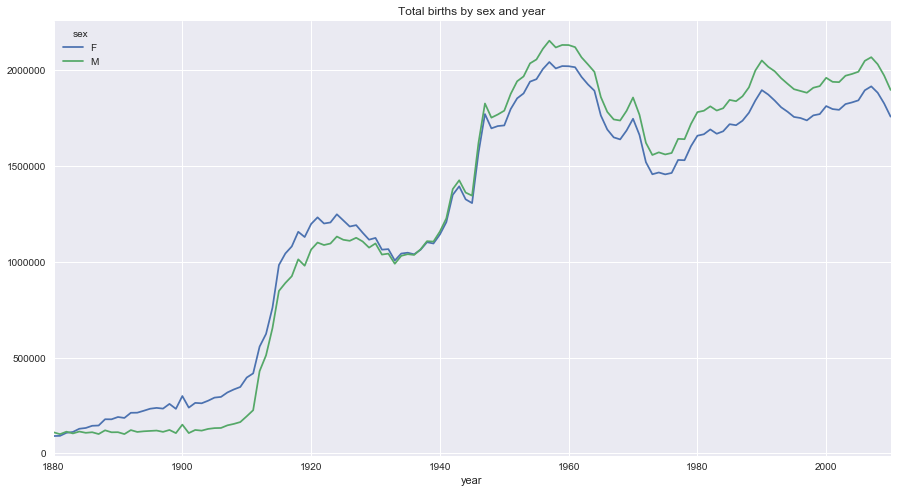
total_births.plot(title='Total births by sex and year', figsize=(15, 8))
下面我们来插入一个prop列,用于存放指定名字的婴儿数相对于总出生数的比列。prop值为0.02表示每100名婴儿中有2名取了当前这个名字。因此,我们先按year和sex分组,然后再将新列加到各个分组上:
def add_prop(group):
group['prop'] = group.births / group.births.sum()
return group
names = names.groupby(['year', 'sex']).apply(add_prop)
names
| name | sex | births | year | prop | |
|---|---|---|---|---|---|
| 0 | Mary | F | 7065 | 1880 | 0.077643 |
| 1 | Anna | F | 2604 | 1880 | 0.028618 |
| 2 | Emma | F | 2003 | 1880 | 0.022013 |
| 3 | Elizabeth | F | 1939 | 1880 | 0.021309 |
| 4 | Minnie | F | 1746 | 1880 | 0.019188 |
| ... | ... | ... | ... | ... | ... |
| 1690779 | Zymaire | M | 5 | 2010 | 0.000003 |
| 1690780 | Zyonne | M | 5 | 2010 | 0.000003 |
| 1690781 | Zyquarius | M | 5 | 2010 | 0.000003 |
| 1690782 | Zyran | M | 5 | 2010 | 0.000003 |
| 1690783 | Zzyzx | M | 5 | 2010 | 0.000003 |
1690784 rows × 5 columns
在执行这样的分组处理时,一般都应该做一些有效性检查(sanity check),比如验证所有分组的prop的综合是否为1。由于这是一个浮点型数据,所以我们应该用np.allclose来检查这个分组总计值是否够近似于(可能不会精确等于)1:
names.groupby(['year', 'sex']).prop.sum()
year sex
1880 F 1.0
M 1.0
1881 F 1.0
M 1.0
1882 F 1.0
...
2008 M 1.0
2009 F 1.0
M 1.0
2010 F 1.0
M 1.0
Name: prop, Length: 262, dtype: float64
这样就算完活了。为了便于实现进一步的分析,我们需要取出该数据的一个子集:每对sex/year组合的前1000个名字。这又是一个分组操作:
def get_top1000(group):
return group.sort_values(by='births', ascending=False)[:1000]
grouped = names.groupby(['year', 'sex'])
top1000 = grouped.apply(get_top1000)
# Drop the group index, not needed
top1000.reset_index(inplace=True, drop=True)
如果喜欢DIY的话,也可以这样:
pieces =[]
for year, group in names.groupby(['year', 'sex']):
pieces.append(group.sort_values(by='births', ascending=False)[:1000])
top1000 = pd.concat(pieces, ignore_index=True)
top1000
| name | sex | births | year | prop | |
|---|---|---|---|---|---|
| 0 | Mary | F | 7065 | 1880 | 0.077643 |
| 1 | Anna | F | 2604 | 1880 | 0.028618 |
| 2 | Emma | F | 2003 | 1880 | 0.022013 |
| 3 | Elizabeth | F | 1939 | 1880 | 0.021309 |
| 4 | Minnie | F | 1746 | 1880 | 0.019188 |
| ... | ... | ... | ... | ... | ... |
| 261872 | Camilo | M | 194 | 2010 | 0.000102 |
| 261873 | Destin | M | 194 | 2010 | 0.000102 |
| 261874 | Jaquan | M | 194 | 2010 | 0.000102 |
| 261875 | Jaydan | M | 194 | 2010 | 0.000102 |
| 261876 | Maxton | M | 193 | 2010 | 0.000102 |
261877 rows × 5 columns
接下来针对这个top1000数据集,我们就可以开始数据分析工作了
1 Analyzing Naming Trends(分析命名趋势)
有了完整的数据集和刚才生成的top1000数据集,我们就可以开始分析各种命名趋势了。首先将前1000个名字分为男女两个部分:
boys = top1000[top1000.sex=='M']
girls = top1000[top1000.sex=='F']
这是两个简单的时间序列,只需要稍作整理即可绘制出相应的图标,比如每年叫做John和Mary的婴儿数。我们先生成一张按year和name统计的总出生数透视表:
total_births = top1000.pivot_table('births', index='year',
columns='name', aggfunc=sum)
total_births
| name | Aaden | Aaliyah | Aarav | Aaron | Aarush | Ab | Abagail | Abb | Abbey | Abbie | ... | Zoa | Zoe | Zoey | Zoie | Zola | Zollie | Zona | Zora | Zula | Zuri |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| year | |||||||||||||||||||||
| 1880 | NaN | NaN | NaN | 102.0 | NaN | NaN | NaN | NaN | NaN | 71.0 | ... | 8.0 | 23.0 | NaN | NaN | 7.0 | NaN | 8.0 | 28.0 | 27.0 | NaN |
| 1881 | NaN | NaN | NaN | 94.0 | NaN | NaN | NaN | NaN | NaN | 81.0 | ... | NaN | 22.0 | NaN | NaN | 10.0 | NaN | 9.0 | 21.0 | 27.0 | NaN |
| 1882 | NaN | NaN | NaN | 85.0 | NaN | NaN | NaN | NaN | NaN | 80.0 | ... | 8.0 | 25.0 | NaN | NaN | 9.0 | NaN | 17.0 | 32.0 | 21.0 | NaN |
| 1883 | NaN | NaN | NaN | 105.0 | NaN | NaN | NaN | NaN | NaN | 79.0 | ... | NaN | 23.0 | NaN | NaN | 10.0 | NaN | 11.0 | 35.0 | 25.0 | NaN |
| 1884 | NaN | NaN | NaN | 97.0 | NaN | NaN | NaN | NaN | NaN | 98.0 | ... | 13.0 | 31.0 | NaN | NaN | 14.0 | 6.0 | 8.0 | 58.0 | 27.0 | NaN |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2006 | NaN | 3737.0 | NaN | 8279.0 | NaN | NaN | 297.0 | NaN | 404.0 | 440.0 | ... | NaN | 5145.0 | 2839.0 | 530.0 | NaN | NaN | NaN | NaN | NaN | NaN |
| 2007 | NaN | 3941.0 | NaN | 8914.0 | NaN | NaN | 313.0 | NaN | 349.0 | 468.0 | ... | NaN | 4925.0 | 3028.0 | 526.0 | NaN | NaN | NaN | NaN | NaN | NaN |
| 2008 | 955.0 | 4028.0 | 219.0 | 8511.0 | NaN | NaN | 317.0 | NaN | 344.0 | 400.0 | ... | NaN | 4764.0 | 3438.0 | 492.0 | NaN | NaN | NaN | NaN | NaN | NaN |
| 2009 | 1265.0 | 4352.0 | 270.0 | 7936.0 | NaN | NaN | 296.0 | NaN | 307.0 | 369.0 | ... | NaN | 5120.0 | 3981.0 | 496.0 | NaN | NaN | NaN | NaN | NaN | NaN |
| 2010 | 448.0 | 4628.0 | 438.0 | 7374.0 | 226.0 | NaN | 277.0 | NaN | 295.0 | 324.0 | ... | NaN | 6200.0 | 5164.0 | 504.0 | NaN | NaN | NaN | NaN | NaN | 258.0 |
131 rows × 6868 columns
接下来使用DataFrame中的plot方法:
total_births.info()
<class 'pandas.core.frame.DataFrame'>
Int64Index: 131 entries, 1880 to 2010
Columns: 6868 entries, Aaden to Zuri
dtypes: float64(6868)
memory usage: 6.9 MB
subset = total_births[['John', 'Harry', 'Mary', 'Marilyn']]
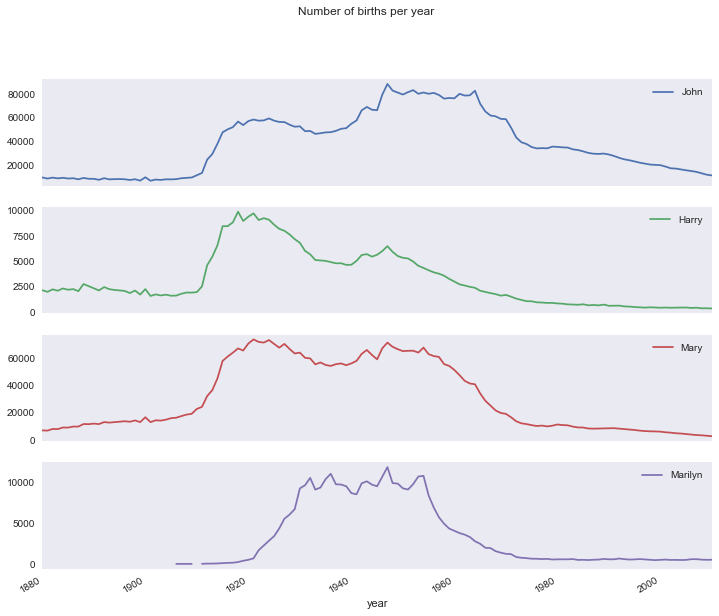
subset.plot(subplots=True, figsize=(12, 10), grid=False,
title="Number of births per year")
array([<matplotlib.axes._subplots.AxesSubplot object at 0x1132a4828>,
<matplotlib.axes._subplots.AxesSubplot object at 0x116933080>,
<matplotlib.axes._subplots.AxesSubplot object at 0x117d24710>,
<matplotlib.axes._subplots.AxesSubplot object at 0x117d70b70>], dtype=object)
评价命名多样性的增长
上图反应的降低情况可能意味着父母愿意给小孩起常见的名字越来越少。这个假设可以从数据中得到验证。一个办法是计算最流行的1000个名字所占的比例,我们按year和sex进行聚合并绘图:
import numpy as np
table = top1000.pivot_table('prop', index='year',
columns='sex', aggfunc=sum)
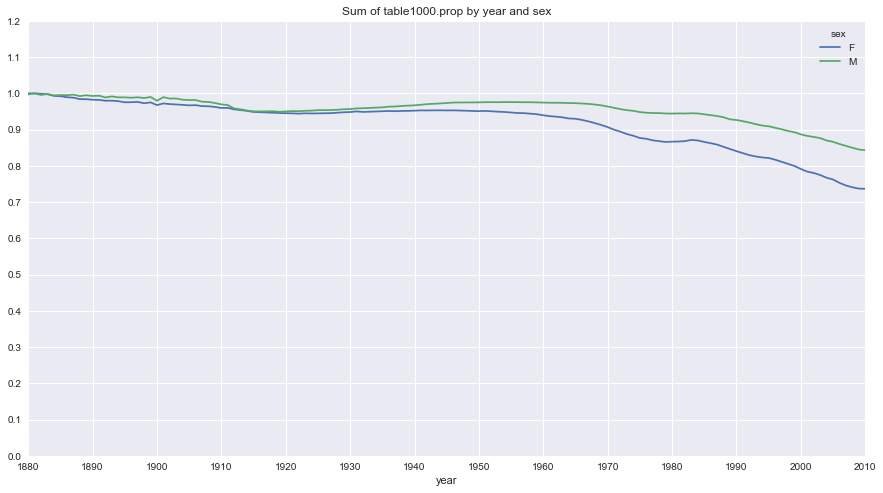
table.plot(title='Sum of table1000.prop by year and sex',
yticks=np.linspace(0, 1.2, 13), xticks=range(1880, 2020, 10),
figsize=(15, 8))
从图中可以看出,名字的多样性确实出现了增长(前1000项的比例降低)。另一个办法是计算占总出生人数前50%的不同名字的数量,这个数字不太好计算。我们只考虑2010年男孩的名字:
df = boys[boys.year == 2010]
df
| name | sex | births | year | prop | |
|---|---|---|---|---|---|
| 260877 | Jacob | M | 21875 | 2010 | 0.011523 |
| 260878 | Ethan | M | 17866 | 2010 | 0.009411 |
| 260879 | Michael | M | 17133 | 2010 | 0.009025 |
| 260880 | Jayden | M | 17030 | 2010 | 0.008971 |
| 260881 | William | M | 16870 | 2010 | 0.008887 |
| ... | ... | ... | ... | ... | ... |
| 261872 | Camilo | M | 194 | 2010 | 0.000102 |
| 261873 | Destin | M | 194 | 2010 | 0.000102 |
| 261874 | Jaquan | M | 194 | 2010 | 0.000102 |
| 261875 | Jaydan | M | 194 | 2010 | 0.000102 |
| 261876 | Maxton | M | 193 | 2010 | 0.000102 |
1000 rows × 5 columns
对prop降序排列后,我们想知道前面多少个名字的人数加起来才够50%。虽然编写一个for循环也能达到目的,但NumPy有一种更聪明的矢量方式。先计算prop的累计和cumsum,,然后再通过searchsorted方法找出0.5应该被插入在哪个位置才能保证不破坏顺序:
prop_cumsum = df.sort_values(by='prop', ascending=False).prop.cumsum()
prop_cumsum[:10]
260877 0.011523
260878 0.020934
260879 0.029959
260880 0.038930
260881 0.047817
260882 0.056579
260883 0.065155
260884 0.073414
260885 0.081528
260886 0.089621
Name: prop, dtype: float64
prop_cumsum.searchsorted(0.5)
array([116])
由于数组索引是从0开始的,因此我们要给这个结果加1,即最终结果为117。拿1900年的数据来做个比较,这个数字要小得多:
df = boys[boys.year == 1900]
in1900 = df.sort_values(by='prop', ascending=False).prop.cumsum()
in1900[-10:]
41853 0.979223
41852 0.979277
41851 0.979330
41850 0.979383
41849 0.979436
41848 0.979489
41847 0.979542
41846 0.979595
41845 0.979648
41876 0.979702
Name: prop, dtype: float64
in1900.searchsorted(0.5) + 1
array([25])
现在就可以对所有year/sex组合执行这个计算了。按这两个字段进行groupby处理,然后用一个函数计算各分组的这个值:
def get_quantile_count(group, q=0.5):
group = group.sort_values(by='prop', ascending=False)
return group.prop.cumsum().searchsorted(q) + 1
diversity = top1000.groupby(['year', 'sex']).apply(get_quantile_count)
diversity = diversity.unstack('sex')
现在,这个diversity有两个时间序列(每个性别各一个,按年度索引)。通过IPython,可以看到其内容,还可以绘制图标
diversity.head()
| sex | F | M |
|---|---|---|
| year | ||
| 1880 | [38] | [14] |
| 1881 | [38] | [14] |
| 1882 | [38] | [15] |
| 1883 | [39] | [15] |
| 1884 | [39] | [16] |
可以看到上面表格中的值为list,如果不加diversity=diversity.astype(float)的话,会报错显示,“no numeric data to plot” error。通过加上这句来更改数据类型,就能正常绘图了:
diversity = diversity.astype('float')
diversity
| sex | F | M |
|---|---|---|
| year | ||
| 1880 | 38.0 | 14.0 |
| 1881 | 38.0 | 14.0 |
| 1882 | 38.0 | 15.0 |
| 1883 | 39.0 | 15.0 |
| 1884 | 39.0 | 16.0 |
| ... | ... | ... |
| 2006 | 209.0 | 99.0 |
| 2007 | 223.0 | 103.0 |
| 2008 | 234.0 | 109.0 |
| 2009 | 241.0 | 114.0 |
| 2010 | 246.0 | 117.0 |
131 rows × 2 columns
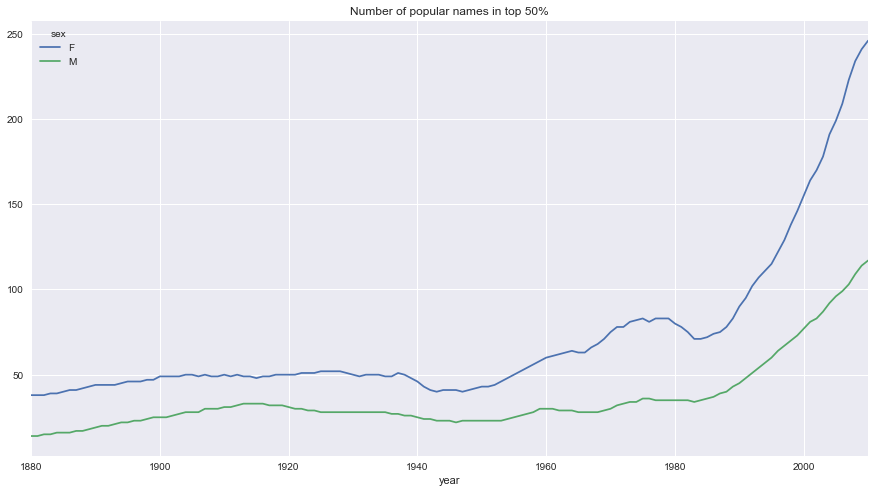
diversity.plot(title='Number of popular names in top 50%', figsize=(15, 8))
从图中可以看出,女孩名字的多样性总是比男孩高,而且还变得越来越高。我们可以自己分析一下具体是什么在驱动这个多样性(比如拼写形式的变化)。
“最后一个字母”的变革
一位研究人员指出:近百年来,男孩名字在最后一个字母上的分布发生了显著的变化。为了了解具体的情况,我们首先将全部出生数据在年度、性别以及末字母上进行了聚合:
# 从name列中取出最后一个字母
get_last_letter = lambda x: x[-1]
last_letters = names.name.map(get_last_letter)
last_letters.name = 'last_letter'
table = names.pivot_table('births', index=last_letters,
columns=['sex', 'year'], aggfunc=sum)
print(type(last_letters))
print(last_letters[:5])
<class 'pandas.core.series.Series'>
0 y
1 a
2 a
3 h
4 e
Name: last_letter, dtype: object
然后,我们选出具有一个代表性的三年,并输出前几行:
subtable = table.reindex(columns=[1910, 1960, 2010], level='year')
subtable.head()
| sex | F | M | ||||
|---|---|---|---|---|---|---|
| year | 1910 | 1960 | 2010 | 1910 | 1960 | 2010 |
| last_letter | ||||||
| a | 108376.0 | 691247.0 | 670605.0 | 977.0 | 5204.0 | 28438.0 |
| b | NaN | 694.0 | 450.0 | 411.0 | 3912.0 | 38859.0 |
| c | 5.0 | 49.0 | 946.0 | 482.0 | 15476.0 | 23125.0 |
| d | 6750.0 | 3729.0 | 2607.0 | 22111.0 | 262112.0 | 44398.0 |
| e | 133569.0 | 435013.0 | 313833.0 | 28655.0 | 178823.0 | 129012.0 |
接下来我们需要安总出生数对该表进行规范化处理,一遍计算出个性别各末字母站总出生人数的比例:
subtable.sum()
sex year
F 1910 396416.0
1960 2022062.0
2010 1759010.0
M 1910 194198.0
1960 2132588.0
2010 1898382.0
dtype: float64
letter_prop = subtable / subtable.sum()
letter_prop
| sex | F | M | ||||
|---|---|---|---|---|---|---|
| year | 1910 | 1960 | 2010 | 1910 | 1960 | 2010 |
| last_letter | ||||||
| a | 0.273390 | 0.341853 | 0.381240 | 0.005031 | 0.002440 | 0.014980 |
| b | NaN | 0.000343 | 0.000256 | 0.002116 | 0.001834 | 0.020470 |
| c | 0.000013 | 0.000024 | 0.000538 | 0.002482 | 0.007257 | 0.012181 |
| d | 0.017028 | 0.001844 | 0.001482 | 0.113858 | 0.122908 | 0.023387 |
| e | 0.336941 | 0.215133 | 0.178415 | 0.147556 | 0.083853 | 0.067959 |
| ... | ... | ... | ... | ... | ... | ... |
| v | NaN | 0.000060 | 0.000117 | 0.000113 | 0.000037 | 0.001434 |
| w | 0.000020 | 0.000031 | 0.001182 | 0.006329 | 0.007711 | 0.016148 |
| x | 0.000015 | 0.000037 | 0.000727 | 0.003965 | 0.001851 | 0.008614 |
| y | 0.110972 | 0.152569 | 0.116828 | 0.077349 | 0.160987 | 0.058168 |
| z | 0.002439 | 0.000659 | 0.000704 | 0.000170 | 0.000184 | 0.001831 |
26 rows × 6 columns
有了这个字母比例数据后,就可以生成一张各年度各性别的条形图了:
import matplotlib.pyplot as plt
fig, axes = plt.subplots(2, 1, figsize=(10, 8))
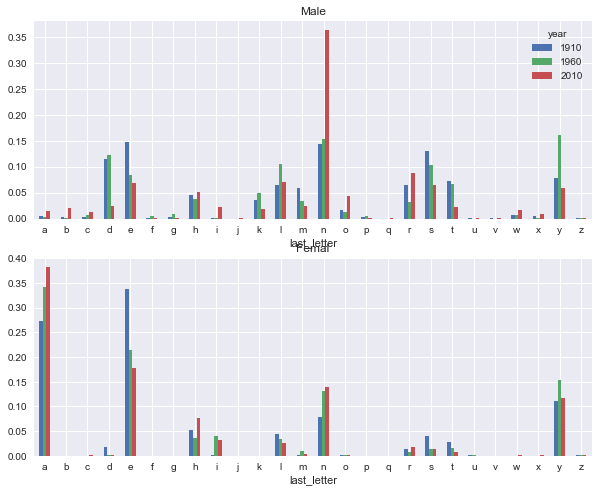
letter_prop['M'].plot(kind='bar', rot=0, ax=axes[0], title='Male')
letter_prop['F'].plot(kind='bar', rot=0, ax=axes[1], title='Femal', legend=False)
从上图可以看出来,从20世纪60年代开始,以字母'n'结尾的男孩名字出现了显著的增长。回到之前创建的那个完整表,按年度和性别对其进行规范化处理,并在男孩名字中选取几个字母,最后进行转置以便将各个列做成一个时间序列:
letter_prop = table / table.sum()
letter_prop.head()
| sex | F | ... | M | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| year | 1880 | 1881 | 1882 | 1883 | 1884 | 1885 | 1886 | 1887 | 1888 | 1889 | ... | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| last_letter | |||||||||||||||||||||
| a | 0.345587 | 0.343440 | 0.338764 | 0.341251 | 0.338550 | 0.341270 | 0.339703 | 0.335258 | 0.332764 | 0.328706 | ... | 0.020162 | 0.020019 | 0.019177 | 0.019505 | 0.018481 | 0.017635 | 0.016747 | 0.016189 | 0.015927 | 0.014980 |
| b | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0.026256 | 0.025418 | 0.024368 | 0.023171 | 0.021645 | 0.020778 | 0.020357 | 0.019655 | 0.019693 | 0.020470 |
| c | NaN | NaN | 0.000046 | 0.000045 | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0.013972 | 0.014048 | 0.014042 | 0.013514 | 0.013083 | 0.012991 | 0.012983 | 0.012458 | 0.012186 | 0.012181 |
| d | 0.006693 | 0.006601 | 0.006806 | 0.007211 | 0.007100 | 0.006478 | 0.006967 | 0.007035 | 0.007266 | 0.007703 | ... | 0.031352 | 0.028794 | 0.027069 | 0.026118 | 0.025420 | 0.025075 | 0.024451 | 0.023574 | 0.023398 | 0.023387 |
| e | 0.366819 | 0.370616 | 0.374582 | 0.373159 | 0.372722 | 0.372896 | 0.372802 | 0.372324 | 0.373675 | 0.373736 | ... | 0.074927 | 0.074603 | 0.073396 | 0.071710 | 0.070799 | 0.069748 | 0.069445 | 0.069362 | 0.068663 | 0.067959 |
5 rows × 262 columns
dny_ts = letter_prop.loc[['d', 'n', 'y'], 'M'].T
dny_ts.head()
| last_letter | d | n | y |
|---|---|---|---|
| year | |||
| 1880 | 0.083055 | 0.153213 | 0.075760 |
| 1881 | 0.083247 | 0.153214 | 0.077451 |
| 1882 | 0.085340 | 0.149560 | 0.077537 |
| 1883 | 0.084066 | 0.151646 | 0.079144 |
| 1884 | 0.086120 | 0.149915 | 0.080405 |
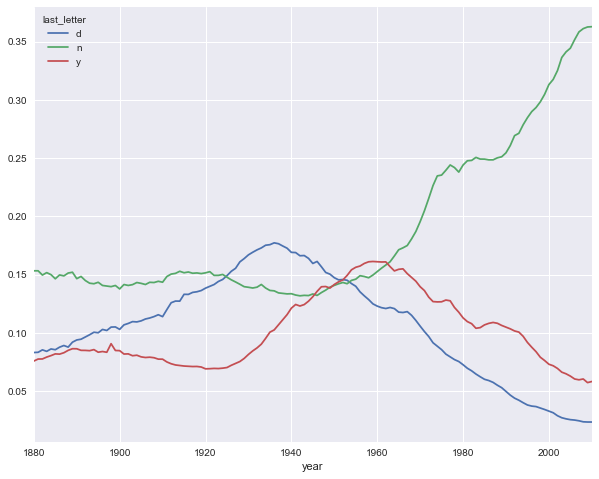
有了这个时间序列的DataFrame后,就可以通过其plot方法绘制出一张趋势图:
dny_ts.plot(figsize=(10, 8))
变成女孩名字的男孩名字(以及相反的情况)
另一个有趣的趋势是,早年流行于男孩的名字近年来“变性了”,列入Lesley或Leslie。回到top1000数据集,找出其中以"lesl"开头的一组名字:
all_names = pd.Series(top1000.name.unique())
lesley_like = all_names[all_names.str.lower().str.contains('lesl')]
lesley_like
632 Leslie
2294 Lesley
4262 Leslee
4728 Lesli
6103 Lesly
dtype: object
然后利用这个结果过滤其他的名字,并按名字分组计算出生数以查看相对频率:
filtered = top1000[top1000.name.isin(lesley_like)]
filtered.groupby('name').births.sum()
name
Leslee 1082
Lesley 35022
Lesli 929
Leslie 370429
Lesly 10067
Name: births, dtype: int64
接下来,我们按性别和年度进行聚合,并按年度进行规范化处理:
table = filtered.pivot_table('births', index='year',
columns='sex', aggfunc='sum')
table = table.div(table.sum(1), axis=0)
table
| sex | F | M |
|---|---|---|
| year | ||
| 1880 | 0.091954 | 0.908046 |
| 1881 | 0.106796 | 0.893204 |
| 1882 | 0.065693 | 0.934307 |
| 1883 | 0.053030 | 0.946970 |
| 1884 | 0.107143 | 0.892857 |
| ... | ... | ... |
| 2006 | 1.000000 | NaN |
| 2007 | 1.000000 | NaN |
| 2008 | 1.000000 | NaN |
| 2009 | 1.000000 | NaN |
| 2010 | 1.000000 | NaN |
131 rows × 2 columns
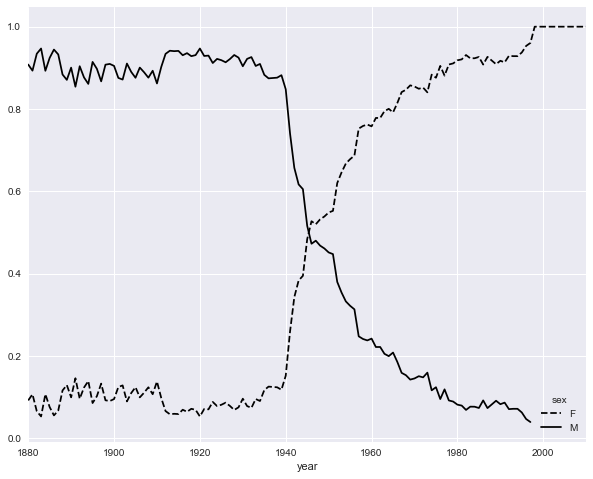
现在,我们可以轻松绘制一张分性别的年度曲线图了:
table.plot(style={'M': 'k-', 'F': 'k--'}, figsize=(10, 8))
<matplotlib.axes._subplots.AxesSubplot at 0x11f0640b8>


![合并区间[中等]](https://img-blog.csdnimg.cn/direct/8195d98576d04e398577815215d22856.png)