大根堆和小根堆配合

实现

第一个数字直接入大根堆

对于后面的数字，

        如果数字 <= 大根堆的堆顶，这个数字入大根堆

        否则入小根堆

在数字入堆的同时，进行大根堆与小根堆的大小的比较，一旦它们两个的大小之差 == 2，较大的堆的堆顶弹出，进较小的堆

目的

保证较小n/2的数在大根堆，保证较大n/2的数在小根堆

各自维持堆顶，利于得到中位数 

偶数个数数字的中位数 = （大根堆的堆顶+小根堆的堆顶）/2

奇数个数数字的中位数 = 个数较大的堆的堆顶

举个栗子

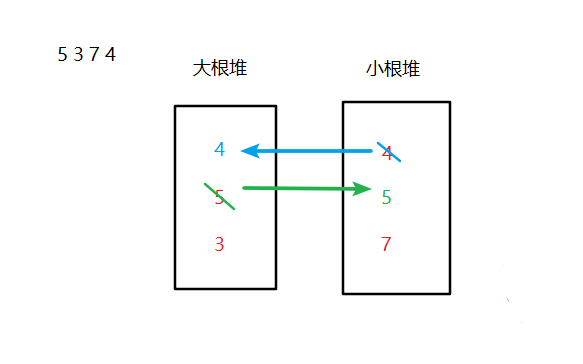
代码

package algorithm;

import java.util.Comparator;
import java.util.PriorityQueue;

public class GetMiddle {
    PriorityQueue<Integer> minPQ = new PriorityQueue<>(new MinComparator());
    PriorityQueue<Integer> maxPQ = new PriorityQueue<>(new MaxComparator());

    public void insert(int num) {
        if (num <= maxPQ.peek()) {
            maxPQ.add(num);
        } else {
            minPQ.add(num);
        }

        if (maxPQ.size() - minPQ.size() == 2) {
            minPQ.add(maxPQ.poll());
        } else if (minPQ.size() - maxPQ.size() == 2) {
            maxPQ.add(minPQ.poll());
        }
    }

    class MinComparator implements Comparator<Integer> {
        @Override
        public int compare(Integer o1, Integer o2) {
            return o1 - o2;
        }
    }

    class MaxComparator implements Comparator<Integer> {
        @Override
        public int compare(Integer o1, Integer o2) {
            return o2 - o1;
        }
    }

    public int getMiddle(int[] arr) {
        if (maxPQ.size() > minPQ.size()) {
            return maxPQ.peek();
        } else if (maxPQ.size() < minPQ.size()) {
            return minPQ.peek();
        } else {
            return (maxPQ.peek() + minPQ.peek()) / 2;
        }
    }

    public static void main(String[] args) {
        int[] arr1 = new int[]{1, 4, 5, 7, 6, 3, 2};

        GetMiddle gm = new GetMiddle();
        gm.maxPQ.add(arr1[0]);
        for (int i = 1; i < arr1.length; i++) {
            gm.insert(arr1[i]);
        }

        System.out.println(gm.getMiddle(arr1));
    }
}