堆的应用（堆排序、Top-K问题）

news2024/9/25 23:24:23

文章目录

1 堆排序
2 Top-K问题

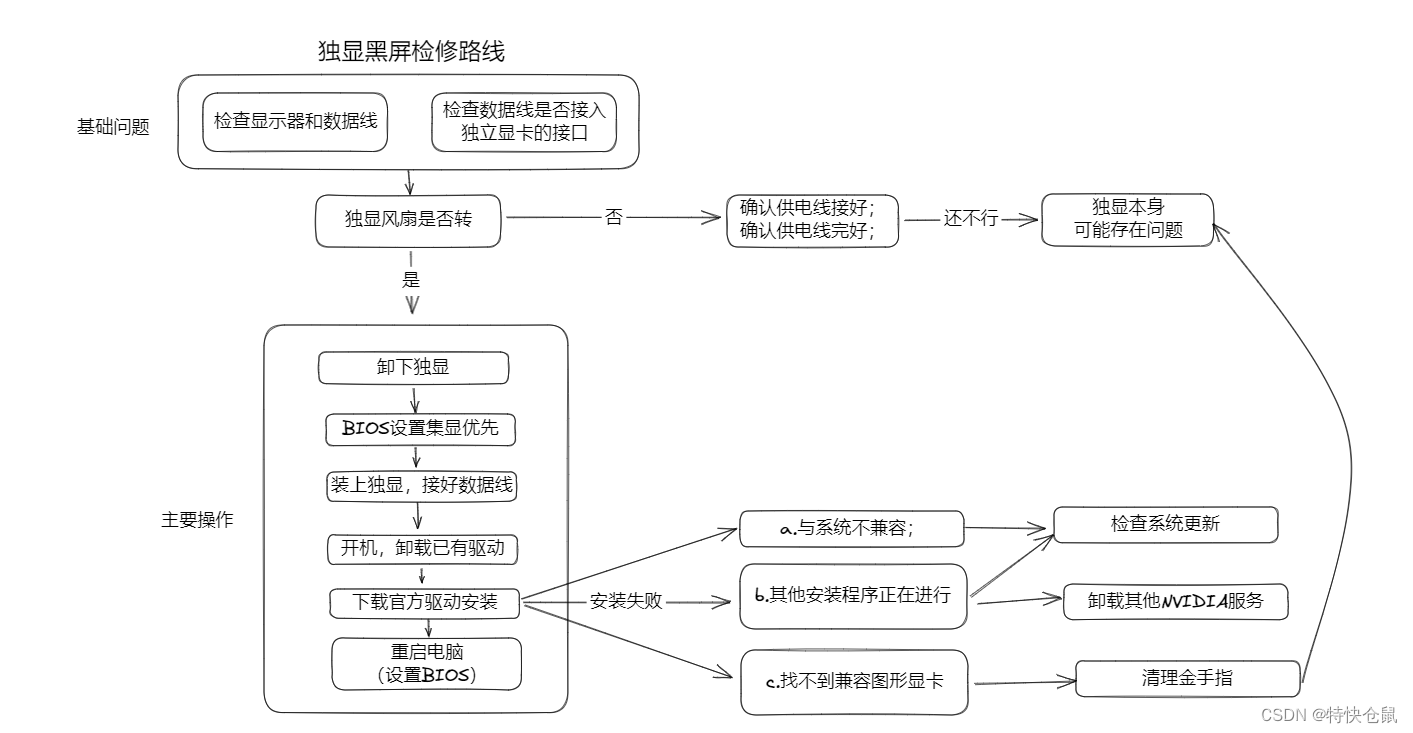
1 堆排序

堆排序是一种基于二叉堆（通常使用数组实现）的排序算法。
它的基本思想是利用堆这种数据结构的性质，通过建立一个堆（大堆或小堆），使得堆的根节点是所有节点中的最大值（大堆）或最小值（小堆）。然后，将根节点与堆的最后一个节点交换，使得最大值或最小值进入有序区。接着，对剩余的未排序部分重新调整成堆，重复这个过程，直到整个数组有序。

建堆和堆调整堆中都用到了向下调整，因此掌握了向下调整法，就可以完成堆排序。对该算法不清楚的，可以参考这篇文章，里面进行了详细的介绍：堆详解(C语言实现)
堆排序步骤：

构建初始堆（建堆）：从最后一个非叶子节点开始，对每个节点进行向下调整（调整成堆的性质，大堆或小堆）。
排升序：建大堆，原因如下：
在堆排序中，升序排序要建立大堆的主要原因是为了保证每次选择堆顶元素都是堆中的最大值。
在排升序时，每次选择堆顶元素与堆的最后一个元素交换，由于堆顶是最大值，将其与末尾元素交换后，最大值就被移到了数组的末尾，而在交换后，需要重新调整堆，使剩余部分重新构成大堆，这样，下一次选择堆顶元素时，依然得到的是剩余元素中的最大值。通过这个过程，每次都能选择到当前堆中的最大值，将其移到数组末尾，逐步形成有序部分，从而实现升序排序。
排降序：建小堆，原因如下：
在堆排序中，降序排序要建立小堆的主要原因是为了保证每次选择堆顶元素都是堆中的最小值。
在排降序时，每次选择堆顶元素与堆的最后一个元素交换，由于堆顶是最小值，将其与末尾元素交换后，最小值就被移到了数组的末尾，而在交换后，需要重新调整堆，使剩余部分重新构成小堆，这样，下一次选择堆顶元素时，依然得到的是剩余元素中的最小值。通过这个过程，每次都能选择到当前堆中的最小值，将其移到数组末尾，逐步形成有序部分，从而实现降序排序。
排序：交换堆的根节点（最大值或最小值）与堆的最后一个节点，并对剩余部分重新调整成堆。
重复：重复步骤2，直到整个数组有序。

例如利用堆排序对该数组{ 8, 5, 3, 9, 1}进行排降序，过程如下：

建小堆
排序

代码如下：

void AdjustDown(int* nums, int n, int parent)
{
	// 左孩子的索引
	int child = parent * 2 + 1;
	// 循环直到没有左孩子
	while (child < n)
	{
		// 如果右孩子存在且比左孩子小，选择右孩子
		//若实现大根堆，这里nums[child + 1] < nums[child]的 ＜ 换成 >
		if (child + 1 < n && nums[child + 1] < nums[child])
		{
			++child;
		}
		// 如果孩子比父亲小，交换它们的值
		//若实现大根堆，这里nums[child] < nums[parent]的 ＜ 换成 >
		if (nums[child] < nums[parent])
		{
			// 孩子比父亲大，堆的有序性已经恢复，退出循环
			int tmp = nums[child];
			nums[child] = nums[parent];
			nums[parent] = tmp;
		}
		else
		{
			break;
		}
		// 更新父亲和孩子的索引
		parent = child;
		child = parent * 2 + 1;
	}
}

void HeapSort(int* nums, int n)
{
	//建堆
	//升序，建大堆
	//降序，建小堆
	for (int i = (n - 2) / 2; i >= 0; --i)
	{
		AdjustDown(nums, n, i);//非叶子节点开始向下调整
	}

	int end = n - 1;
	while (end > 0)
	{
		//交换堆的根节点与堆的最后一个节点
		int tmp = nums[end];
		nums[end] = nums[0];
		nums[0] = tmp;
		//并对剩余部分重新调整成堆。
		AdjustDown(nums, end, 0);
		end--;
	}
}

总之，堆排序是一种选择排序，它利用了堆的性质：堆顶的数据，是堆中最大的数据（或者最小的数据）。该算法通过不断选择堆顶元素，将其与堆的最后一个元素交换，然后调整堆，使剩余部分重新构成堆，重复这个过程直到整个数组有序。

2 Top-K问题

Top-K 问题是在一个包含大量数据的集合中，找出前 K 个最大或最小的元素数据的问题。通常数据量都是比较大的。

关于解决TOP-K问题,我们首先想到的是对这个数据集合拍升序或者降序，然后取前 K 个数据，就能解决这个问题。该方法的缺点是不适用于数据量极大的情况。这是因为，利用排序算法，需要将数据加载到内存中，在内存中进行排序，然而当数据量大到无法一次性加载到内存中时，排序算法的效率就会受到限制。
因此，就有人提出了使用堆来解决这个问题。该算法的思想是：用数据集的前k个数据，建一个大小为 K 的小顶堆（Top K 最大问题）或大顶堆（Top K 最小问题）。依次遍历剩余n - k个元素，将元素与堆顶比较，若大于（或者小于）堆顶，则替换堆顶，并进行堆调整。这样，最终堆中的元素就是前 K 个最大或最小的元素。

例如:面试题 17.14. 最小K个数
过程如下：

用数据集的前k个数据，建一个大小为 K 的小根堆。
依次遍历剩余n - k个元素，将元素与堆顶比较，若大于堆顶，则替换堆顶，并进行堆调整。

代码如下：

 //向下调整算法
 void AdjustDown(int* nums, int n, int parent)
 {
     int child = parent * 2 + 1;
     while (child < n)
     {
         if (child + 1 < n && nums[child + 1] > nums[child])
         {
             ++child;
         }
         if (nums[child] > nums[parent])
         {
             int tmp = nums[child];
             nums[child] = nums[parent];
             nums[parent] = tmp;
         }
         else
         {
             break;
         }
         parent = child;
         child = parent * 2 + 1;
     }
 }
int* smallestK(int* arr, int arrSize, int k, int* returnSize)
{

    int* nums = (int*)malloc(sizeof(int) * k);
    for (int i = 0; i < k; ++i)
    {
        nums[i] = arr[i];
    }
     //前k个数建大堆
    for (int i = (k - 2) / 2; i >=0; --i)
    {
        AdjustDown(nums, k, i);
    }
    //依次遍历剩余n - k个元素
    for (int i = k; i < arrSize; ++i)
    {
        //将元素与堆顶比较，若大于堆顶，则替换堆顶
        if (k > 0 && arr[i] < nums[0])
        {
            nums[0] = arr[i];
            //进行堆调整
            AdjustDown(nums, k, 0);
        }
    }

    *returnSize = k;
    return nums;
}