stdlib.h是做数学计算的头文件
目录
1 数学知识
1.1 弧度值/π = 角度值/180
1.2 双曲函数
2 math.h
2.1 反余弦值 acos()
2.2 反正弦值 asin()
2.3 反正切值 atan()
2.4 两个数的反正切值 atan2()
2.5 向上取整 ceil()
2.6 余弦值 cos()
2.7 双曲余弦 cosh()
2.8 e的x次幂 exp()
2.9 分解浮点数的指数和尾数 frexp()
2.10 分解浮点数的指数和尾数 ldexp()
2.11 ln log()
2.12 lg log10()
2.13 幂运算 pow()
2.14 正弦值 sin()
2.15 双曲正弦 sinh()
2.16 开平方根 sqrt()
2.17 正切值 tan()
2.18 双曲正切 tanh()
1 数学知识
1.1 弧度值/π = 角度值/180
1.2 双曲函数


2 math.h
2.1 反余弦值 acos()

![]()
1.04 / 3.14 * 180 ≈ 59.6 ≈ 60
arccos(1/2) = 60°
2.2 反正弦值 asin()

![]()
0.52 / 3.14 * 180 ≈ 29.8 ≈ 30
arcsin(1/2) = 30°
2.3 反正切值 atan()

![]()
0.7853 / 3.14 * 180 ≈ 45
arctan(1) = 45°
2.4 两个数的反正切值 atan2()
比如我现在求 arctan([根号3]/3)

![]()
0.52 / 3.14 * 180 ≈ 29.8 ≈ 30
arcsin([根号3]/3) = 30°
2.5 向上取整 ceil()

![]()
2.6 余弦值 cos()

1.04 / 3.14 * 180 ≈ 59.6 ≈ 60
cos(60°) = 1/2
![]()
2.7 双曲余弦 cosh()
cosh(x) = (e^x + e^-x) / 2

cosh(1) ≈ (2.7 + 0.37)/2 = 1.535
![]()
2.8 e的x次幂 exp()
比如我算e的1次幂

![]()
2.9 分解浮点数的指数和尾数 frexp()
frexp()用的是下面这个公式
![]()
我们让value为5.5,求mantissa与exponent

![]()
5.5 = 0.6875 * 2的3次方
2.10 分解浮点数的指数和尾数 ldexp()
ldexp()用的是下面这个公式


44 = 5.5 * 2的3次方
![]()
2.11 ln log()


![]()
2.12 lg log10()

![]()
- 计算器里显示的log()实际上是lg()
![]()
2.13 幂运算 pow()
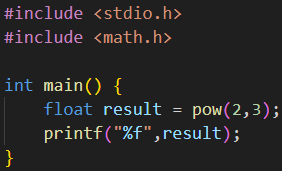
![]()
2.14 正弦值 sin()
0.52 / 3.14 * 180 ≈ 29.8 ≈ 30

sin(30°) = 1/2
![]()
2.15 双曲正弦 sinh()
![]()
sinh(x) = (e^x - e^-x) / 2
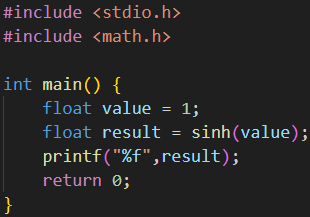
sinh(1) ≈ (2.7 - 0.37)/2 = 1.165
![]()
2.16 开平方根 sqrt()

根号25 = 5
![]()
2.17 正切值 tan()
0.7853 / 3.14 * 180 ≈ 45

tan(45°) = 1
![]()
2.18 双曲正切 tanh()
tanh(x) = (e^x - e^-x) / (e^x + e^-x)

tanh(1) ≈ (2.7 - 0.37)/(2.7 + 0.37) = 2.33/3.07 ≈ 0.7589
![]()



![[SWPU2019]你有没有好好看网课? 1](https://img-blog.csdnimg.cn/10b4b480fa5042d88250d605aacb4f44.png)