A/B 实验的核心统计学理论是(双样本)假设检验,是用来判断样本与样本、样本与总体的差异是由 抽样误差 引起还是 本质差别 造成的一种统计推断方法。
假设检验,顾名思义,是一种对自己做出的假设进行数据验证的过程。通俗地说,假设检验是一门 做出拒绝 的理论,检验结果有两种:拒绝原假设(reject H0),无法拒绝原假设(fail to reject H0)。实验者往往将主观不希望看到的结果(新策略没有效果)置于 原假设 (从英文命名就可以看出来感情色彩 - 它叫 null hypothesis),而将原假设的互斥事件,即对事实本身有利的结果(新策略有提升)置于 备则假设 (alternative hypothesis),如此构成的假设检验目的在于用现有的数据通过一系列理论演绎 拒绝原假设 ,达到证明备择假设是正确的,即某项改进有效的目的,所以这一套方法也被称作 null hypothesis significance testing (NHST) 。
由于我们永远只能抽取流量做 小样本 实验,所以每个假设检验都面临着 随机抽样误差 ,因此在做出推论的过程中,一切都围绕 概率 展开。这意味着没有任何一个基于假设检验的演绎过程可以对结果 100%确定。但所幸,统计理论可以告诉我们在每一步中犯错的机会。因此,事先知晓我们 可能犯什么错 ,以及 有多大机会犯错 就成了设计和解读假设检验的关键所在。
实验者在假设检验的过程中可能会做出 两类错误判断 - 不意外地 - 它们被命名为 第一类错误 (弃真)和 第二类错误 (取伪)。第一类错误(Type I Error):H0 为真,拒绝 H0。“本身没提升,但误判为有提升”第二类错误(Type II Error):H1 为真,接受 H0。“本身有提升,但没有察觉提升”
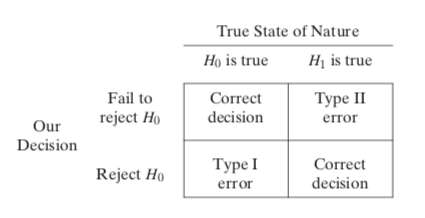
对比上图,第一类错误指的是原假设正确但是我们做出了拒绝原假设的结论,这个错误在现实中常常表现为“我作出了统计显著的结论但是我的改动实际上没用”;相应地,第二类错误指的是原假设错误但是我们没能拒绝原假设,这个错误在现实中常常表现为“我的改动有效,但实验没能检测出来”。
在 AB 实验的场景下,如果对某一个新 feature 是否有效进行假设检验,H0 为新 feature 没有效果,第一类错误指的是“新 feature 实际无效但检测出存在显著性效果”,第二类错误则指的是“新 feature 实际有效但未能检测出效果”。如果犯了第一类错误,会导致新 feature 的错误上线,可能会带来实际利益损失,如果犯了第二类错误,实际有效的 feature 将不会上线,带来的是潜在利益的损失。两相比较,应该更严格地控制第一类错误发生的概率。
定性知晓我们可能犯什么错以后,我们仍然需要定量地分析有多大机会犯错。在频率统计学中 ,显著性水平(α) 以及 (1 - 检验效力 power)(beta) 分别描述了实验者犯第一类错误和第二类错误的概率。这两个统计指标结合在一起比较完整地刻画一个假设检验的总体基本性能,也是进行一个假设检验所需统计指标的最小集。应该说,缺少任何一个,我们都没有足够的信息作出科学的推论,甚至可能错误影响产品的走向。
适用范围可以对 单个总体参数(H0:μ=c) 或者 两个总体参数(H0: μ1= μ2) 进行检验,假设的内容可以是双侧检验 如参数是否等于某个值(H0:μ=c),也可以为单侧检验如 参数是否大于或小于某个值(H0:μ><c)。在 AB 实验的背景下,我们通常进行的检验是 两总体双侧检验。
检验步骤
-
提出假设:H0: μ1= μ2v.s. H1: μ1!= μ2
-
构造统计量
-
计算统计量、检验阈值、置信区间及 p 值
-
得出结论:若 p<0.05 或统计量绝对值>阈值或置信区间包含 0,则拒绝原假设;若 p>0.05 或统计量绝对值<=阈值或置信区间不包含 0,则无法拒绝原假设。
Note:有些其他的计算公式会假定两组的总体方差相等,在方差的计算方式上有区别,这类公式不推荐,因为该假设在 AB 实验应用中并不常见。
p-valueP 值就是当原假设为真是所得到的样本观察结果或更极端结果出现的概率。如果 P 值很小,说明这种情况发生的概率很小,但如果出现了,根据小概率原理,我们就有理由拒绝原假设。P 值越小,说明实验发现的差异是因为抽样误差导致的概率越小,极大程度上还是由于本质上存在差异造成,我们拒绝原假设的理由越充分。
注: 两样本均值差的置信区间包含 0 等价于 P 值大于 0.05 ,此时接受原假设。思想上 与区间估计的原理中提到的“对称”有相通之处。两样本均值差的置信区间包含 0 等价于 均值差与 0 的距离小于 1.96 倍标准差 等价于 统计量的绝对值小于 1.96 等价于 P 值大于 0.05
DataTester 是火山引擎数智平台旗下产品,能基于先进的底层算法,提供科学分流能力和智能的统计引擎,支持多种复杂的 A/B 实验类型。DataTester 深度耦合推荐、广告、搜索、UI、产品功能等多种业务场景需求,为业务增长、转化、产品迭代、策略优化、运营提效等各个环节提供科学的决策依据,让业务真正做到数据驱动。
DataTester 经过抖音、今日头条等字节业务多年验证,截至 2022 年 8 月,已在字节跳动内部累计完成 150 万次 A/B 实验。此外也已经服务了美的、得到、凯叔讲故事等在内多家标杆客户,将成熟的“数据驱动增长”经验赋能给各行业。