零膨胀泊松回归分析

计数研究模型中，常用泊松回归模型，但泊松回归模型理论上是要求平均值与标准差相等，如果不满足，则可使用负二项回归模型

在实际研究中，会出现一种情况即因变量为计数变量，并且该变量包括非常多的数字0，当出现此种情况下，此时可考虑使用零膨胀泊松回归模型，也或者零膨胀负二项回归模型。零膨胀模型的特点是将模型分为两阶段进行（即设置为混合分布模型），第1阶段（零膨胀阶段）为计数变量是否为0的拟合，SPSSAU默认使用二元logit模型进行拟合，第2阶段为泊松分布模型拟合。零膨胀泊松回归模型如下所示：

 

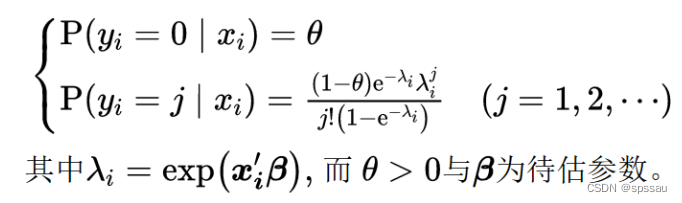
零膨胀泊松回归模型分为两个阶段，第1阶段即零膨胀阶段可拟合因变量是否为0，此阶段中可放入一些自变量X用于拟合因变量是否取数字0的模型，当然也可不放入；第2阶段放入的自变量X为真实研究的变量项。

实际研究中，如果因变量中出现较多的数字0时，则可使用零膨胀泊松回归进行研究，当然还可以使用零膨胀负二项回归模型。至于零膨胀泊松回归模型与零膨胀负二项回归模型的选择上，建议可结合AIC或BIC信息准则进行判断，以信息准则值较小的模型作为最终模型。除此之外，相关文献中还使用Vuong检验进行判断，该检验在学术研究中受到置疑问，SPSSAU暂未来提供该检验（具体可参考下述文献: Wilson P . The misuse of the Vuong test for non-nested models to test for zero-inflation[J]. Economics Letters, 2015.）。

---

1 背景

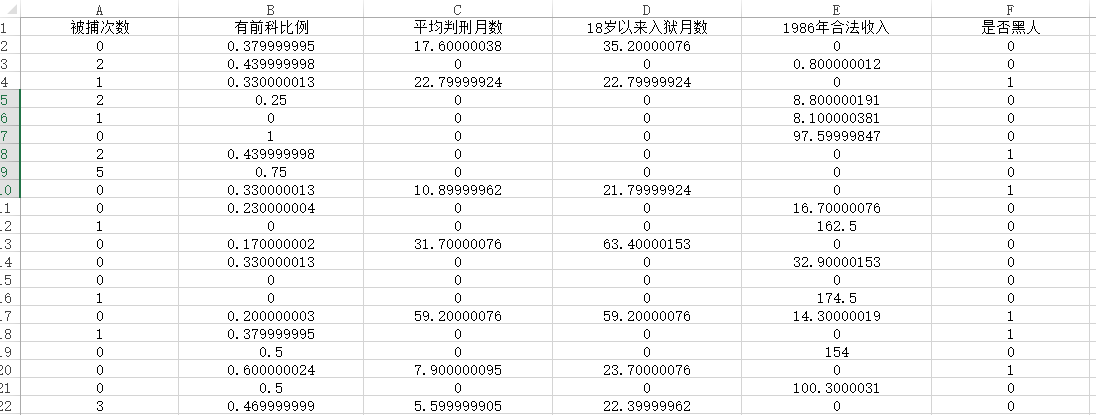
当前有一份关于美国犯罪率的研究，数据包括被捕次数，该变量为计数变量，并且包括大量的数字0（即被捕次数为0），除此之外，包括另外5个自变量，分别是‘有前科比例’、‘平均判邢月数’、‘18岁以来入狱月数’、‘1986年合法收’和‘是否黑人’，其中是否黑人这项，使用数字1表示黑人，数字0表示不是黑人。部分数据截图如下：

2 理论

零膨胀泊松回归模型研究X对于Y的影响，且Y为计数变量且Y包括较多的数字0。除此之外，零膨胀泊松回归模型分为两个阶段，第1阶段为判断Y是否为0的二元logit模型，第1阶段中可包括影响Y是否为数字0的影响因素X，当然也可没有（如果没有此为常数）；第2阶段为真实的研究模型。

特别提示：

• 很多时候需要零膨胀泊松回归模型与零膨胀负二项回归模型进行选择对比使用，建议结合模型输出的AIC或BIC信息准则，以该两值较小值对应的模型作为最终模型。
• 研究中也可考虑首先过滤掉数字0然后进行普通泊松回归（甚至OLS回归研究），但此种做法会丢失大量有意义样本。

3 操作

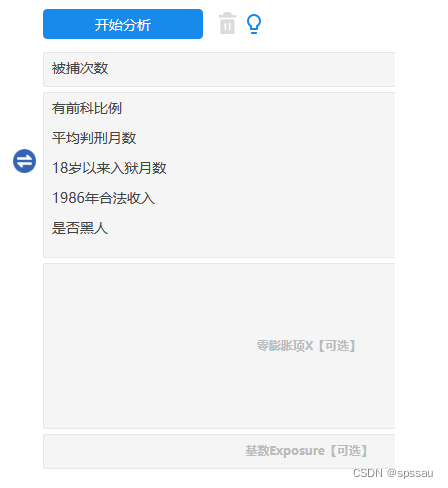
本例子中研究被捕次数的影响因素，其中影响因素包括‘有前科比例’、‘平均判邢月数’、‘18岁以来入狱月数’、‘1986年合法收’和‘是否黑人’，操作截图如下。

本案例时第1阶段零膨胀模型并不包括任何影响因素，因而‘零膨胀项X【可选】’框留空，不放入分析项。与此同时，本案例数据为原始数据并非带‘基数Exposure’格式数据，因而基数项框留空。

 

4 SPSSAU输出结果

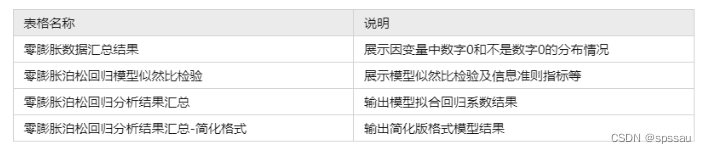
零膨胀泊松回归模型一共输出4个表格，说明如下：

 

5文字分析

上表格展示‘被捕次数’的数字0分布情况，从上表格可以看到，共计2725个样本中有72.29%为数字0，因而意味着应该使用零膨胀模型较为适合。

 

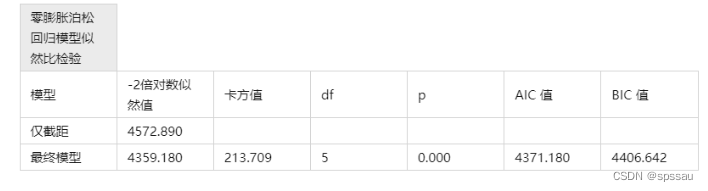
从上表格可以看到：模型通过似然比检验(χ2 =213.709, p =0.000<0.05)，即意味着模型构建有意义。除此之外，上表格展示出AIC值和BIC值，如果需要进行模型对比选优，可使用该两个指标，该两个指标值越小越好。

 

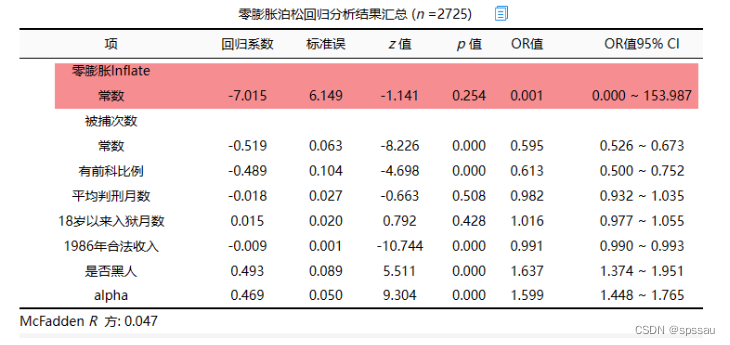
上表格展示出零膨胀泊松回归结果，首先零膨胀模型中仅列出常数值，因为本案例中零膨胀模型并没有设置影响‘被捕次数’是否为0的影响因素项。

从上表格可以看到：有前科比例呈现出0.01水平的显著性，回归系数值为-0.489，即意味着有前科比例越高时，被捕次数反倒越少。与此同时，合法收入也呈现出0.01水平的显著性，该项回归系数为-0.009<0，即意味着合法收越高的群体，其被捕次数越低。是否黑人这项的回归系数为0.493并且呈现出0.01水平的显著性，即说明相对来讲，黑人群体被捕次数明显会更高。与此同时，平均判刑月数、18岁以来入狱月数这两项对于被捕次数并没有影响关系，p值均大于0.05。

SPSSAU针对模型回归系数进行简化格式展示，如上表格所示。

6 剖析

零膨胀泊松分析涉及以下几个关键点，分别如下：

• 首先需确保因变量包括较多的数字0，如果不是这样，此时应使用普通的泊松模型即可；
• 如果需要在零膨胀泊松回归模型或者零膨胀负二项回归模型之间进行取值，建议结合AIC或BIC信息准则越小越好原理进行决择即可。
• 零膨胀模型时共有两个阶段，第1阶段为零膨胀模型即研究因变量是否为0的模型，该模型中也可放入影响因素X，不放入时则该模型中仅有常数；第2阶段模型为真实研究和关注的模型。