【题目描述】
一个工厂制造的产品形状都是长方体，它们的高度都是h，长和宽都相等，一共有六个型号，他们的长宽分别为1×1,2×2,3×3,4×4,5×5,6×6。这些产品通常使用一个6×6×h的长方体包裹包装然后邮寄给客户。因为邮费很贵，所以工厂要想方设法的减小每个订单运送时的包裹数量。他们很需要有一个好的程序帮他们解决这个问题从而节省费用。现在这个程序由你来设计。

【输入】
输入包括几行，每一行代表一个订单。每个订单里的一行包括六个整数，中间用空格隔开，分别为1×1至6×6这六种产品的数量。输入将以6个0组成的一行结尾。

【输出】
除了输入的最后一行6个0以外，输入文件里每一行对应着输出文件的一行，每一行输出一个整数代表对应的订单所需的最小包裹数。

【输入样例】

0 0 4 0 0 1
7 5 1 0 0 0
0 0 0 0 0 0

【输出样例】

2
1

思路分析：

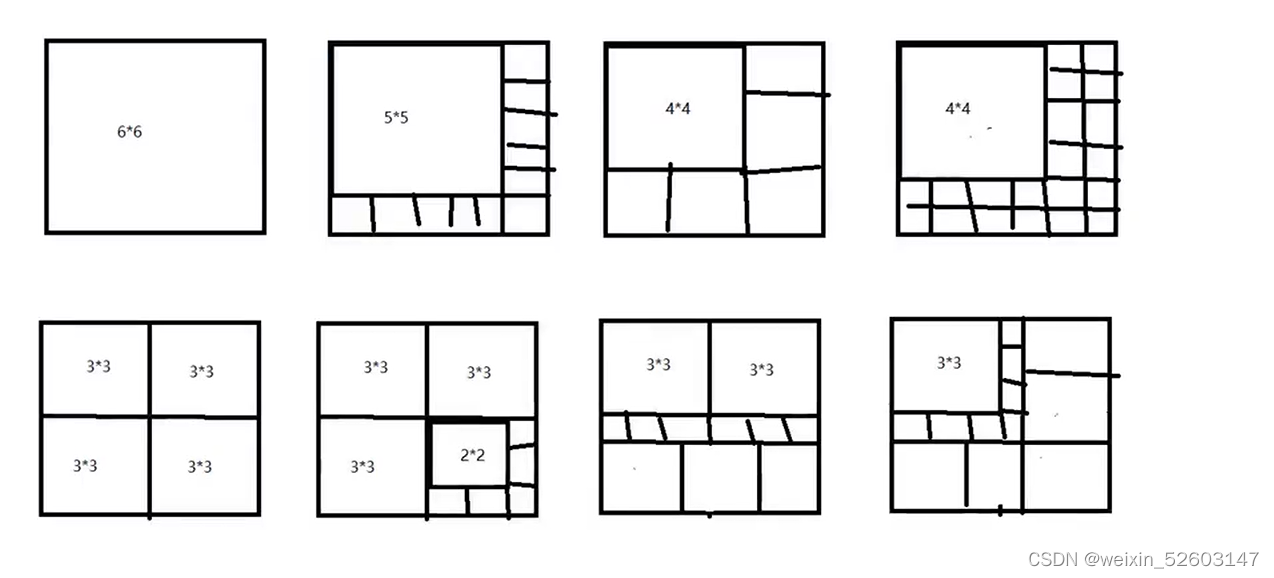
根据上图可以知道6x6，5x5，4x4 这些只要有就需要单独的开辟一个包裹进行包装。利用ans来统计一共多少的包裹，首先找到6x6，5x5，4x4这些一共有多少个，就是需要多少的包裹ans+=a[6]+a[5]+a[4]; ，接下来开始计算3x3的长方体，3x3不能塞到以上已经有的情况中（6x6，5x5，4x4）， 所以需要再单独统计3x3的情况。根据上图一个包裹最多只可以装进4个33,所以向上取整看看装下所有的3x3的长方体需要多少的包裹ans+=ceil(a[3]/4.0);。上面的情况统计完成之后，开始统计2x2的情况，这是我们发下2x2是可以塞进之前统计的情况的，我们开始计算可以塞进的多少的2x2的长方体记录到num2_2中。判断a[2]的数量是不是能全部塞进去，如果塞不进去需要另外增加新的包裹，一个新的包裹最多可塞下9个2x2，ans+=ceil((a[2]-num2_2)/9.0); 。继续开始统计11的长方体，以上的所有已经增加的包裹看看有多少个空可以塞入1x1的包裹，num1_1来统计可以塞的数量num1_1=36*ans-36*a[6]-25*a[5]-16*a[4]-9*a[3]-4*a[2];,判断a[1]的数量是不是够塞进去，不够塞入则需要增加新的包裹ans+=ceil((a[1]-num1_1)/36.0);。最后的到的ans就是包裹的数量。

#include<bits/stdc++.h>
using namespace std;
int a[7];//统计每一个n*n的长度有多少个
int ans;//统计答案最后有多少个包裹
int num1_1,num2_2;//表示每一种情况有多少的1*1,2*2可以放下
int main(){
	while(1){
		int cnt=0;//统计输入了多少个0，题目最后的输入全部是0
		ans=0;//初始化最终包裹数量
		num1_1=num2_2=0;
		for(int i=1;i<=6;i++){
			cin>>a[i];
			if(!a[i]) cnt++;//计算一共多少输入0
		}
		if(cnt==6) break;//表示输入全部为0，结束输入
		//开始判断,判断6*6，5*5，4*4的长方体有多少个，因为这些必须单独开出一个
		ans+=a[6]+a[5]+a[4];
		//开始判断3*3的情况，3*3也不可以直接拼到前面的情况中
		ans+=ceil(a[3]/4.0);//根据画图我们可以得到3*3的一个包裹最多可装4个所以向上取整，看多少个包裹
		int temp=0;//统计3*3的每一种情况可以放多少2*2
		if(a[3]%4==3) temp=1;
		if(a[3]%4==2) temp=3;
		if(a[3]%4==1) temp=5;
		//开始计算前面的情况下可以塞下的2*2的个数
		//6*6 的个数可以塞 0个 ， 5*5 可以塞0个
		//4*4 的个数可以塞 5个 ， 3*3 根据个数可以塞 temp个
		num2_2= a[4]*5+temp;//计算出可塞多少的2*2
		if(a[2]>num2_2){//塞进所有的2*2不够塞
		//不够塞需要多加包裹
			ans+=ceil((a[2]-num2_2)/9.0);
		}
		//算出上面所有的情况后可以塞入多少的1*1
		num1_1=36*ans-36*a[6]-25*a[5]-16*a[4]-9*a[3]-4*a[2];
		if(a[1]>num1_1){
			ans+=ceil((a[1]-num1_1)/36.0);
		}
		cout<<ans<<endl;
		
	}	
}