通常,MATLAB中绘制三维曲面图,先要生成网格数据,再调用mesh函数和surf函数绘制三维曲面。若曲面用含两个自变量的参数方程定义,则还可以调用fmesh函数和fsurf函数绘图。若曲面用隐函数定义,则可以调用fimplicit3函数绘图。
01、三维曲面
1. 产生网格坐标矩阵
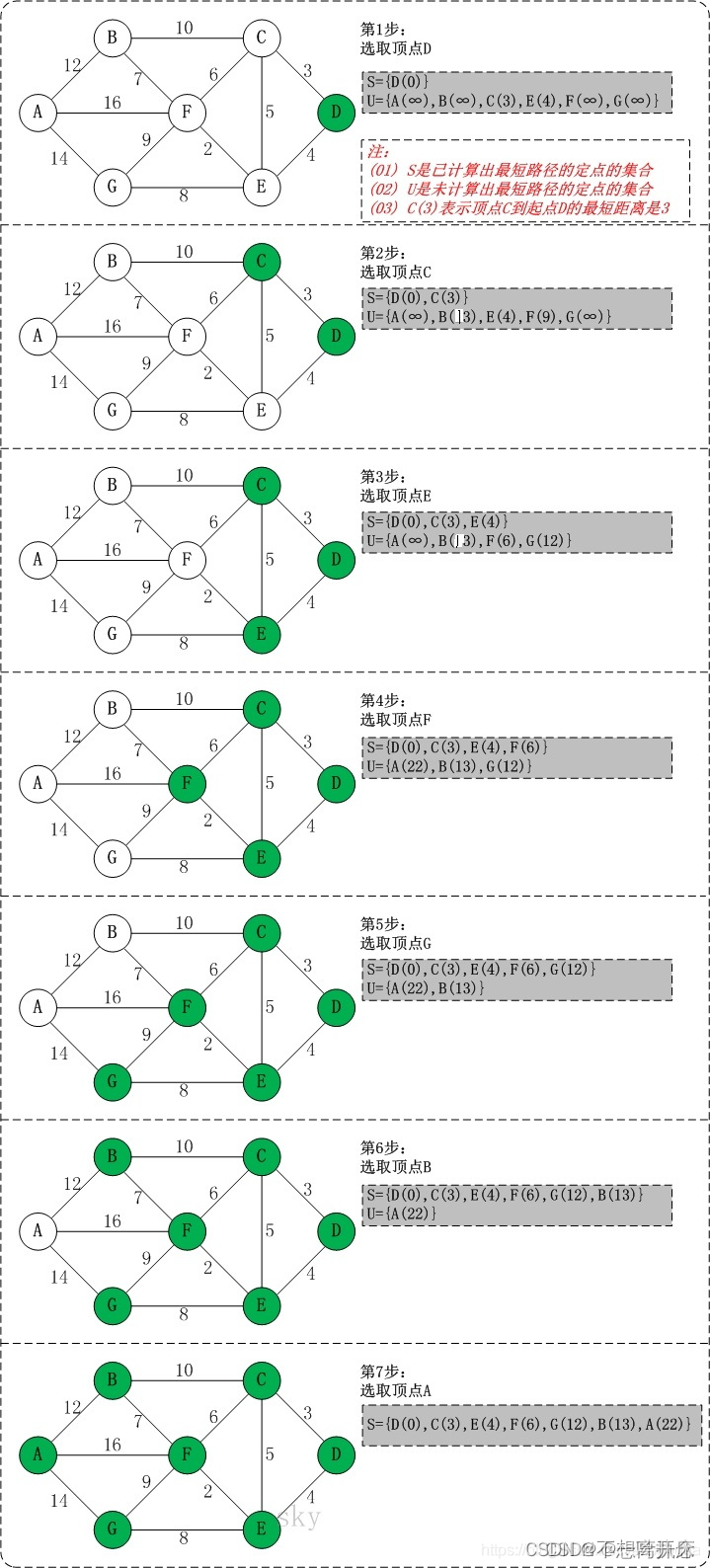
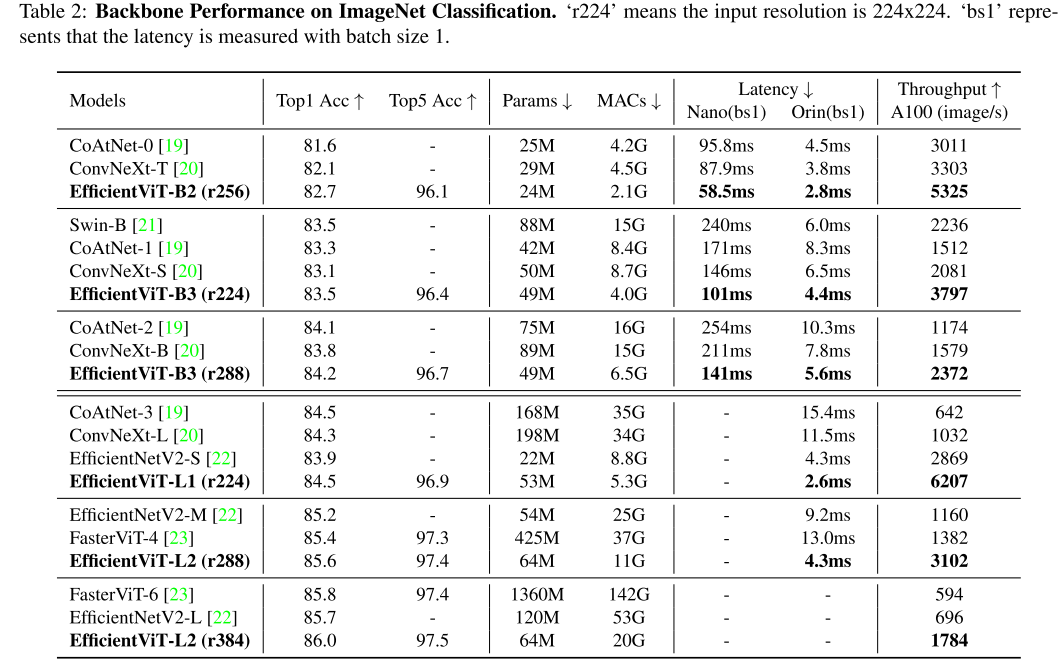
在MATLAB中产生二维网格坐标矩阵的方法是: 将x方向区间[a,b]分成m份,将y方向区间[c,d ]分成n份,由各划分点分别作平行于两坐标轴的直线,将区域[a,b]×[c,d]分成m×n个小网格,生成代表每一个小网格顶点坐标的网格坐标矩阵。例如,在xy平面选定一矩形区域,如图1所示,其左下角顶点的坐标为(2,3),右上角顶点的坐标为(6,8)。然后在x方向分成4份,在y方向分成5份,由各划分点分别作平行于两坐标轴的直线,将区域分成5×4个小矩形,总共有6×5个顶点。用矩阵X、Y分别存储每一个网格顶点的x坐标与y坐标,矩阵X、Y就是该矩形区域的xy平面网格坐标矩阵。
■ 图1网格坐标示例在MATLAB中,产生平面区域内的网格坐标矩阵有两种方法。
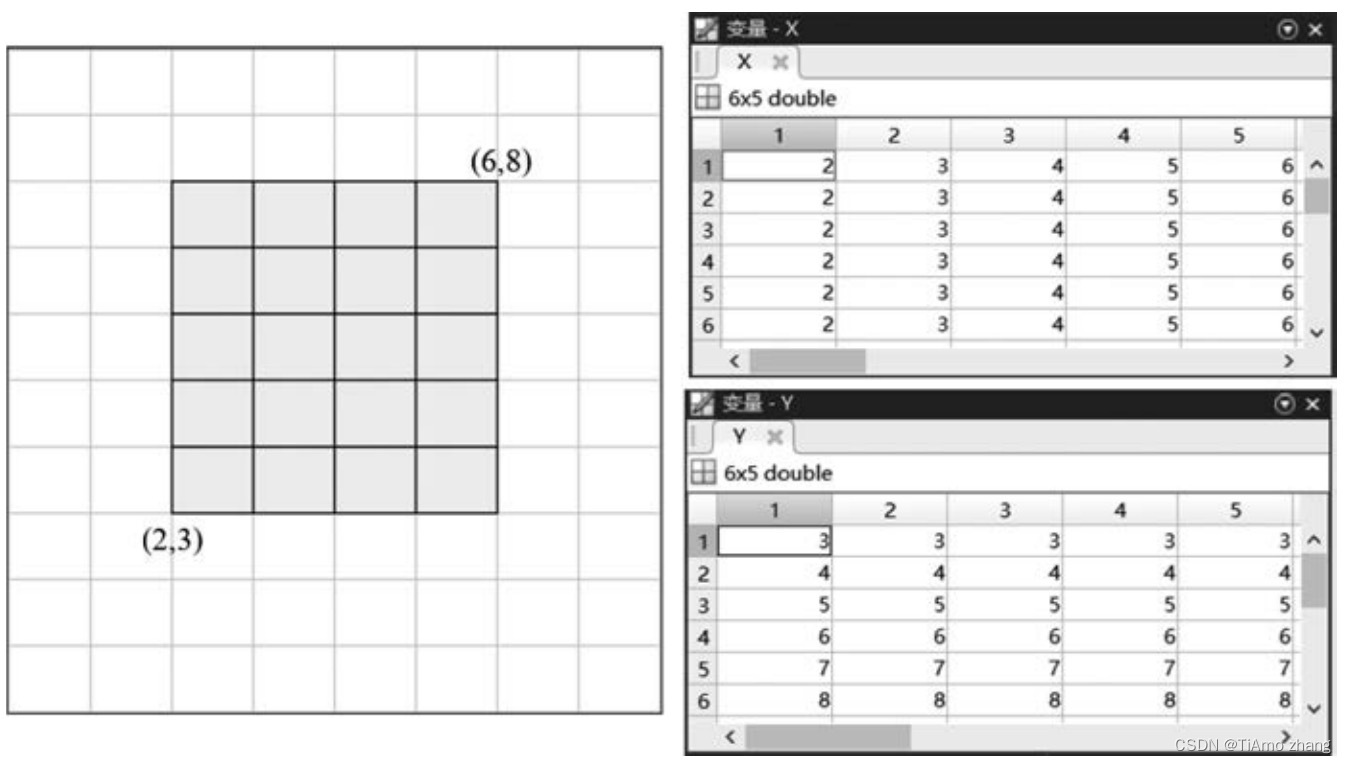
(1) 利用矩阵运算生成。例如,生成图5-24中的网格坐标矩阵,使用以下命令:

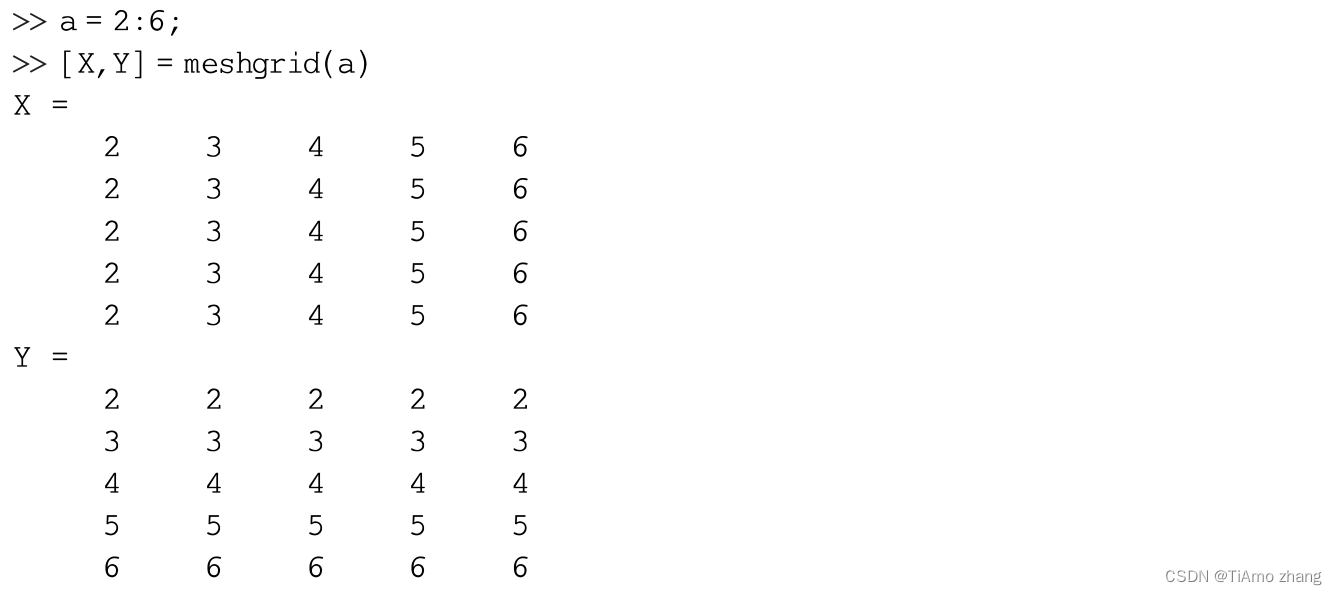
(2) 调用meshgrid函数生成二维网格坐标矩阵,函数的调用格式如下:
其中,输入参数x、y为向量,输出参数X、Y为矩阵。命令执行后,矩阵X的每一行都是向量x,行数等于向量y的元素的个数; 矩阵Y的每一列都是向量y,列数等于向量x的元素的个数。矩阵X和Y相同位置上的元素(Xij,Yij)存储二维空间网格顶点(i,j)的坐标。例如,生成图1中的网格坐标矩阵,也可以使用以下命令:

函数参数可以只有一个,此时生成的网格坐标矩阵是方阵,例如:
meshgrid函数也可以用于生成三维网格数据,调用格式如下:
[X,Y,Z] = meshgrid(x,y,z)其中,输入参数x、y、z为向量,输出参数X、Y、Z为三维数组。命令执行后,数组X、Y和Z的第一维大小和向量x元素的个数相同,第二维大小和向量y元素的个数相同,第三维大小和向量z元素的个数相同。X、Y和Z相同位置上的元素(Xijk,Yijk,Zijk)存储三维空间网格顶点(i,j,k)的坐标。
ndgrid函数用于生成n维网格数据,调用格式如下:
[X1,X2,...Xn] = ndgrid(x1,x2,...xn)其中,输入参数x1、x2、…、xn为向量,输出参数X1、X2、…、Xn为n维矩阵。例如:

对比前面meshgrid网格数据会发现,meshgrid网格数据进行转置即得到ndgrid网格数据。
2. mesh函数和surf函数
MATLAB提供了mesh函数和surf函数来绘制三维曲面图。mesh函数用于绘制三维网格图,网格线条有颜色,网格线条之间无颜色; surf函数用于绘制三维曲面图,网格线条之间的补面用颜色填充。surf函数和mesh函数的调用格式为:
mesh(x,y,z,c)
surf(x,y,z,c)通常,输入参数x、y、z是同型矩阵,x、y定义网格顶点的xy平面坐标,z定义网格顶点的高度。选项c用于指定在不同高度下的补面颜色。c缺省时,MATLAB认为c=z,即颜色的设定值默认正比于图形的高度,这样就可以绘制出层次分明的三维图形。当x,y是向量时,要求x的长度等于矩阵z的列数,y的长度等于矩阵z的行数,x、y向量元素的组合构成网格顶点的x、y坐标。
【例1】已知
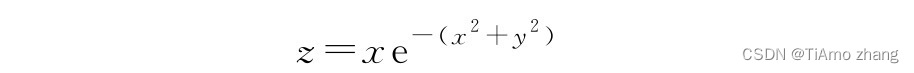
其中,x、y的40个值均匀分布在[-2,2]范围内,绘制三维曲面图。
程序如下
x = linspace(-2,2,40);
[xx,yy] = meshgrid(x);
zz = xx * exp(-(xx^2 + yy^2));
mesh(xx,yy,zz);
title('mesh');
xlabel('X');
ylabel('Y');
zlabel('Z');程序运行结果如图2所示。mesh、surf函数的前两个参数x、y也可以是行向量或列向量,所以程序中的mesh函数也可以写成mesh(x,x,zz)。
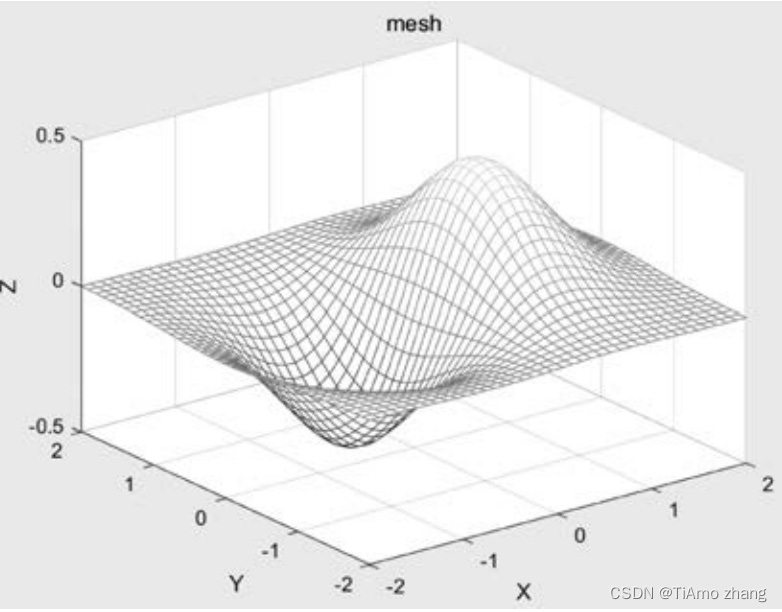
■ 图2 三维曲面图
若调用surf、mesh函数时,省略前两个输入参数x、y,则把z矩阵的第二维下标当作x坐标,把z矩阵的第一维下标当作y坐标,然后绘制三维曲面图。例如:
>>t = 1 : 5;
>>z = [0.5*t;2*t;3*t];
>>mesh(z);第二条命令生成的z是一个3×5的矩阵,执行mesh(z)命令绘制图形,曲面各个顶点的x坐标是z元素的列下标,y坐标是z元素的行下标。
此外,还有两个和mesh函数功能相似的函数,即meshc函数和meshz函数,其用法与mesh函数类似,不同的是meshc函数还在xy平面上绘制曲面在z轴方向的等高线,meshz函数还在xy平面上绘制曲面的底座。surf函数也有两个类似的函数,即具有等高线的曲面函数surfc和具有光照效果的曲面函数surfl。
【例2】在xy平面内选择区域[-8,8]×[-8,8],利用下列函数绘制4种形式的三维曲面图。
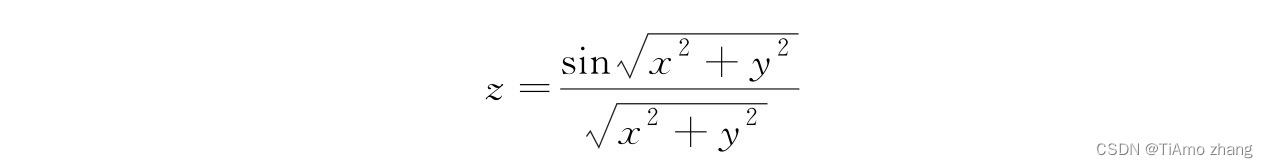
程序如下:
[x,y] = meshgrid(-8:0.5:8);
z = sin(sqrt(x^2+y^2))/sqrt(x^2+y^2);
subplot(2,2,1);
meshz(x,y,z);
title(meshz(x,y,z));
subplot(2,2,2);
meshc(x,y,z);
title(meshc(x,y,z));
subplot(2,2,3);
surfl(x,y,z);
title(surfl(x,y,z));
subplot(x,y,z);
title(surfc(x,y,z));程序运行结果如图3所示。
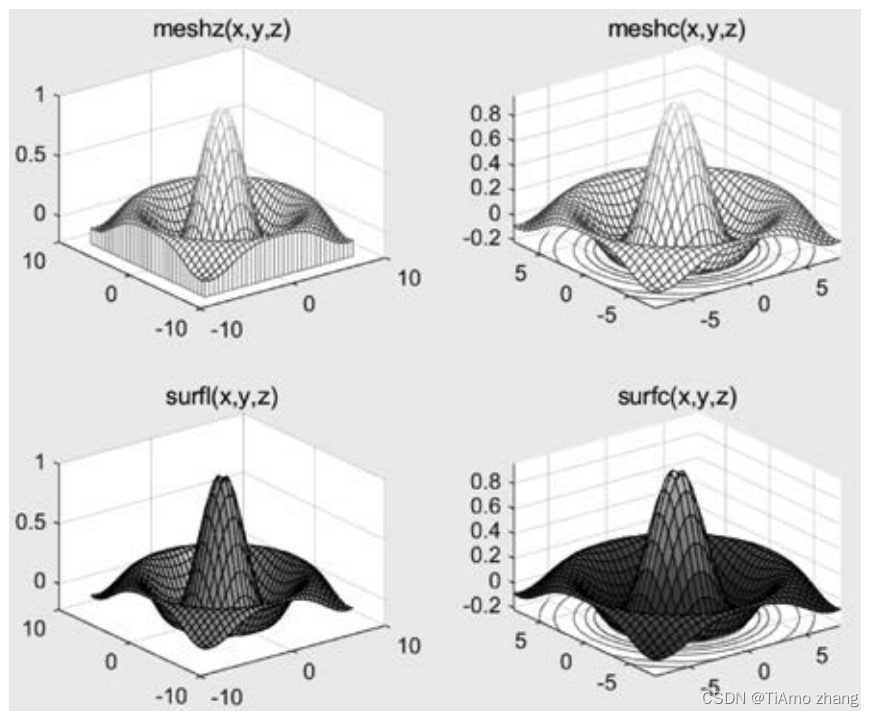
■ 图3 4种形式的三维曲面图