第一题：

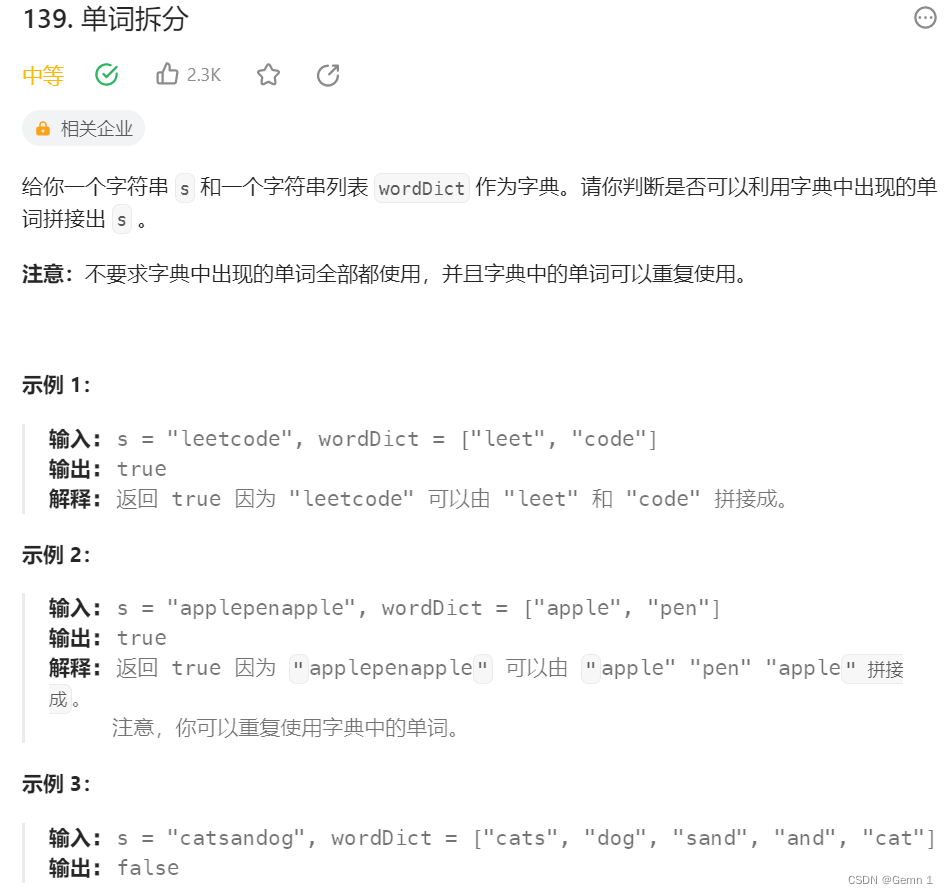
简介：

本题的重点在于确定背包容量和物品数量

1. 确定dp数组以及下标的含义

dp[i] : 字符串长度为i的话，dp[i]为true，表示可以拆分为一个或多个在字典中出现的单词。 

     2.确定递推公式

如果确定dp[j] 是true，且 [j, i] 这个区间的子串出现在字典里，那么dp[i]一定是true。（j < i ）。

所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。

     3.dp数组如何初始化

dp[0]初始为true完全就是为了推导公式。下标非0的dp[i]初始化为false，只要没有被覆盖说明都是不可拆分为一个或多个在字典中出现的单词。

    4.确定遍历顺序

题目中说是拆分为一个或多个在字典中出现的单词，所以这是完全背包。两种遍历顺序都可以，因为我们只要确定能够拼成就行

1. 举例推导dp[i]

以输入: s = "leetcode", wordDict = ["leet", "code"]为例，dp状态如图：

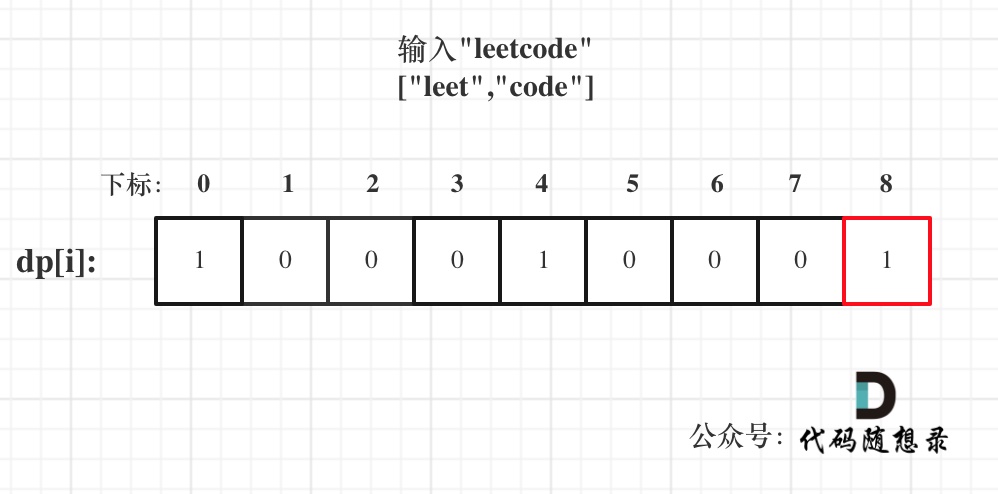
代码实现：

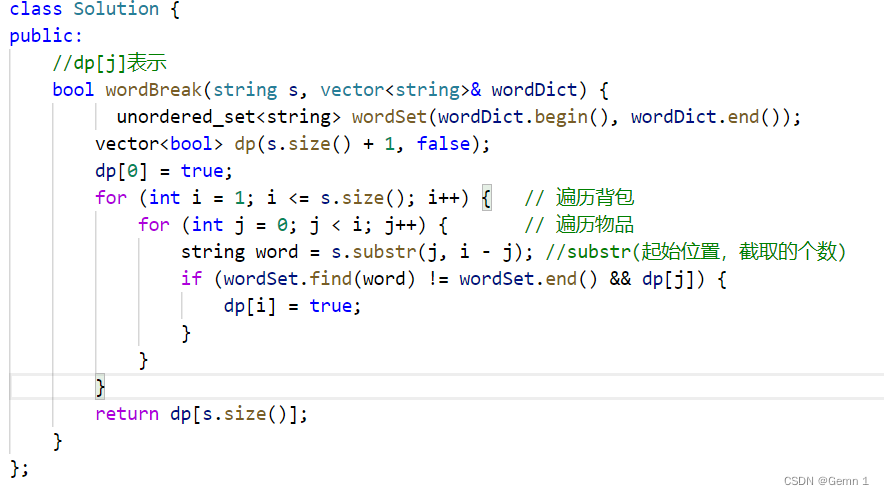
第二题：

简介：

本题时纯多重背包的应用，但是其实和01背包的区别在于他的物品有个数，一个物品可能有多个。我们只要将其全部展开就可以了。

代码实现： 

#include <iostream>
#include <vector>
using namespace std;
void testbag(){
    int bagWeight,n;
    cin >> bagWeight >> n;
    vector<int> weight(n, 0); 
    vector<int> value(n, 0);
    vector<int> nums(n, 0);
    for (int i = 0; i < n; i++) cin >> weight[i];
    for (int i = 0; i < n; i++) cin >> value[i];
    for (int i = 0; i < n; i++) cin >> nums[i];    
    vector<int> dp(bagWeight+1,0);
    for(int i=0;i<n;i++){
        for(int j=bagWeight;j>=weight[i];j--){
            //遍历个数
            for(int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++)
               dp[j]=max(dp[j],dp[j-k*weight[i]]+k*value[i]);
        }
    }
    
    cout << dp[bagWeight] << endl;
}





int main(){
    testbag();
}

总结： 

有些题还是有点抽象，需要多加练习，提高对题的敏感程度。继续加油！