引言
在学习高级知识时,理解基本概念至关重要。为什么?因为基础知识是您构建高级知识的基础。如果你把更多的东西放在薄弱的基础之上,它最终可能会分裂,这意味着你最终无法完全理解你所学的任何知识。因此,让我们尝试深入了解基本原理。
在本系列中,我将解释机器学习中的概率和统计。主要来自教科书:Simon J.D. Prince博士的《Computer Vision: Models, Learning, and Inference》。这本教科书很棒而且切中要害。 在我的这一系列文章中,我将总结并添加一些额外的想法,以便您轻松掌握这些概念。
概率和随机变量简介
我相信你在某个时候已经了解了概率。我们在现实生活中做决定时也会不自觉地使用它。如果您认为自己最有可能在您试图做出的决定中取得成功,那么您就会去做。否则,你不会。这是一个有趣的研究领域,但有时也很棘手。因此,在本文的这一部分,让我们回顾一下什么是概率,并向您介绍“随机变量”的概念。
假设您手上有一张牌。而你即将卡片抛到地上。卡片躺在地上时正面朝上的概率是多少?
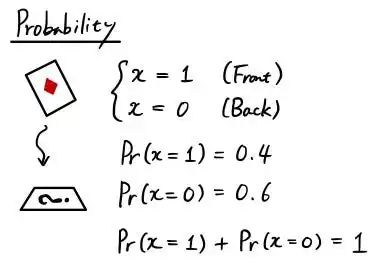
概率在现实生活中通常用 % 表示(比如 80% 的下雨几率),但是当我们在数学中处理概率时,我们通常用小数来表示它们(例如 0.5 表示 50%)。概率衡量事件发生的可能性,用 0 到 1 之间的数字表示。
随机变量(RV)代表我们感兴趣结果的变量。当我们谈到上面丢卡片的示例时。 随机变量x用来表示一张牌的状态。它只有 2 种状态,面朝上 (x = 1) 或面朝下 (x = 0)。如果您熟悉编程,它就像您将使用的任何其他变量一样。每次事件发生时,RV 都可以更改其状态。所以如果你丢了一张牌 5 次,x 可能是 [0, 0, 1, 0, 1]。由于我们在 5 次试验中有 3 次面朝下 (x = 0),因此一张牌面朝下的概率为 Pr(x=0) = 3/5 = 0.6。另一方面,一张牌面朝上 (x = 1) 的概率是 5 次中的 2 次,因此 Pr(x=1) = 2/5 = 0.4。请注意,所有状态(x = 0 和 x = 1)的总和为 1,如果对所有可能的状态求和,情况总是如此。
概率密度函数简介 (PDF)
现在你知道什么是概率和随机变量了。再来说说概率密度函数(通常缩写为PDF,不是你经常使用的文件类型!)。
还记得我向您展示过所有状态的总和始终为 1 吗?记住这一点非常重要,因为它是一个非常有用的依赖属性。
如果我要在条形图中可视化丢卡片的示例,它会是这样的:
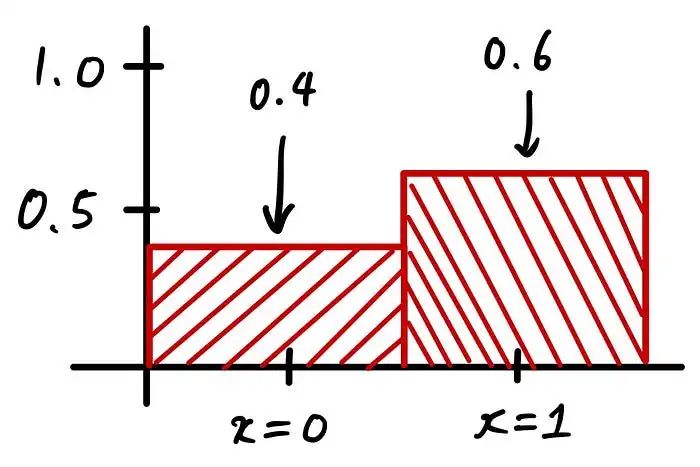
这是概率密度函数的离散版本。称为概率质量假设每个条形的宽度始终为 1。那么 Pr(x=0) 的面积为 0.4 * 1 = 0.4。Pr(x=1) 也是如此。请注意,所有区域的总和始终为 1。如果是连续的,同样适用。
让我们在这里回顾一下什么是连续和离散概率分布函数。
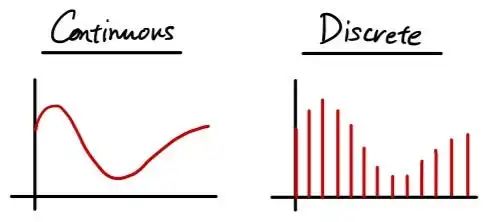
这两个图都代表相同的分布。唯一的区别是它是连续的还是离散的。在数据科学中,尤其是当我们通过编程处理数据时,您更有可能处理具有多行和多列的离散数据,每个单元格包含一个数据点。
联合概率简介
我们讨论了概率和概率密度分布以及连续和离散数据表示。现在让我们更深入地探讨一下概率,谈谈“联合概率”。
下面我们来看一个简单的例子。假设你有 2 个随机变量 x 和 y,x 代表是否下雨,y 代表你是否有雨伞。假设您知道每个事件的概率:

目前,这两个条件是相互独立的。但是我们想知道它们同时发生的概率。这就是“联合概率”发挥作用的地方。
让我们举个例子。下雨而你有伞的概率是多少?(感谢上帝,你有雨伞!)这是我们的案例 1。我们有 Pr(x=1, y=1) 的联合概率,x=1 表示下雨的可能性,y=1 表示你有雨伞。情况 2 是最坏的情况。下雨了,你没有带伞。联合概率为 Pr(x=1, y=0)。
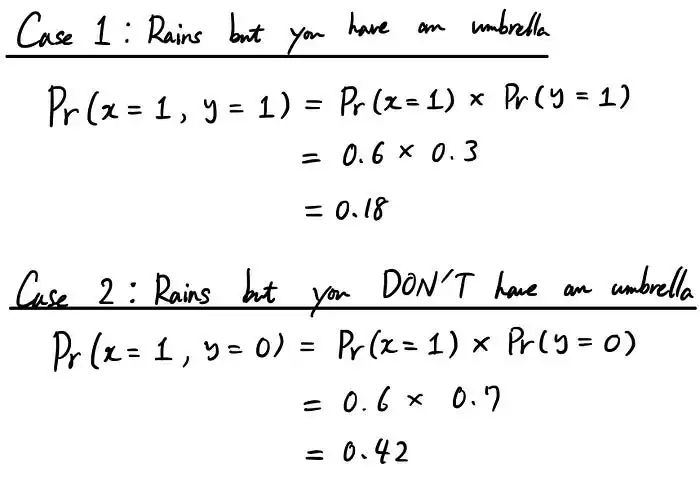
所以通过上面的例子,我希望你对什么是联合概率有一点了解。用更一般的术语来说,联合概率是计算两个(或更多!)事件在同一时间点一起发生的可能性的大小。
为了给你另一个视角,让我们试着可视化什么是联合概率。假设你有 2 个随机变量(x 和 y)并且想直观地知道它的联合概率。它看起来像下面的例子。

把它想象成等高线图。深色区域(接近黑色)位于底部,随着颜色变浅(接近黄色),海拔高度也变高。本质上,您是在尝试通过查看 2D 地图来了解3D视图。
那么,当涉及到联合概率时,这告诉我们什么?一件重要的事情是黑色方框包围的整个区域始终等于 1。还记得我们讨论过概率密度函数 (PDF) 吗?面积必须始终为 1 , 这里也一样。既然是概率,那么这里所有可能的联合概率之和就得是1。还有一个方面就是高度。你可以看到在中心附近有一个淡黄色的部分,稍微偏右一点。这是 Pr(x, y) 的联合概率最高的地方,这意味着特定的 x 和 y 对会为特定事件产生更高的概率。
边缘概率简介
好了,现在你知道联合概率了。我们来谈谈“边缘化”。边缘化是从联合概率到我们一开始处理的标准概率的一种方式。假设您只有联合概率:
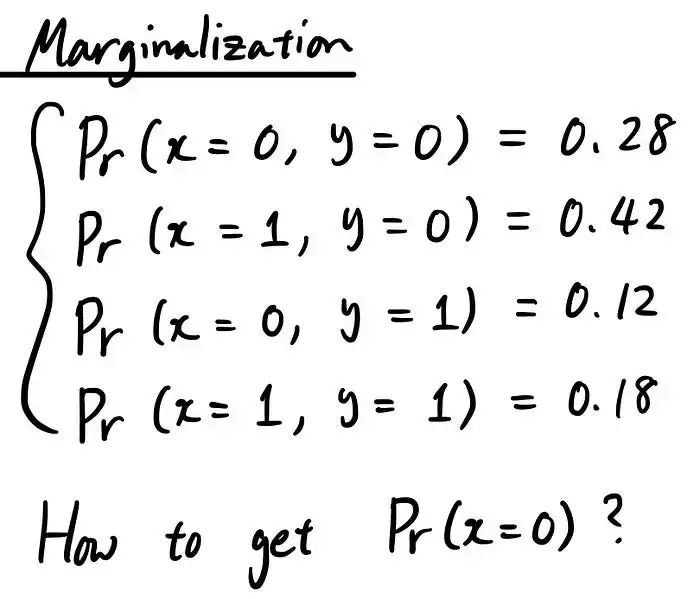
我们现在感兴趣的是独立概率,例如 Pr(x=1) 或 Pr(y=0)。我们如何从这些联合概率中计算出来?
这很容易。这是连续和离散情况的公式:
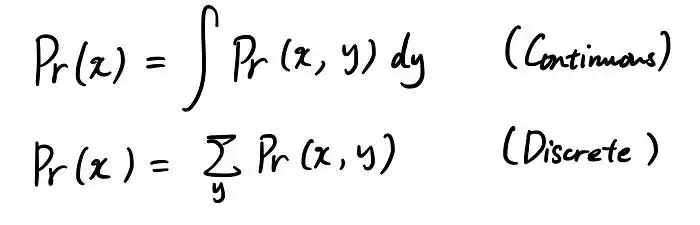
它只是对不感兴趣的随机变量的所有可能状态进行求和。让我们看一个例子来理解这一点。假设你想得到 Pr(x=0),但你只有联合概率 Pr(x=0, y=0) & Pr(x=0, y=1)。要获得 Pr(x=0),您可以通过执行以下操作来执行边缘化:
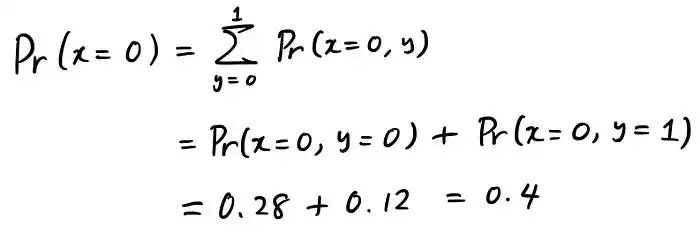
那么这个计算背后的直觉是什么?Marginalization 是试图为你感兴趣的状态考虑所有可能的情况。要想得到 Pr(x=0)。问题是你只有联合概率 Pr(x=0, y=0) 和 Pr(x=0, y=1)。但是如果你想一想,对于我们感兴趣的特定状态 (x=0),只有两种情况。 无非 y=0 还是 y=1。这就是为什么将Pr(x=0, y=0) 和Pr(x=0, y=1) 的概率相加,我们在考虑Pr(x=0) 的所有可能情况,从而得到概率。
条件概率简介
现在话题会变得有点复杂,但同时也更有趣!先说一个很重要的概念,叫做“条件概率”。
让我们再次回到下雨和打伞的例子。以前,我们认为每个状态都是独立的,这意味着一个条件不会影响另一个。考虑到下午可能会下雨的情况(假设),你带伞的可能性会增加。这就是条件概率发挥作用的地方。

所以条件概率如下所示:

这个等式是什么意思呢?
回到可视化的联合概率等高线图,我们可以解释为什么这个等式有意义。我已经解释过联合概率看起来像左边的等高线图。条件概率是在给定一定条件(y = y*)的情况下进行限制。在这种情况下,您不是在考虑所有可能的 y,而只是考虑特定的 y=y* 来作为您的决定的基础(例如,当您已经知道下午可能会下雨时,您正试图考虑带上雨伞 ).
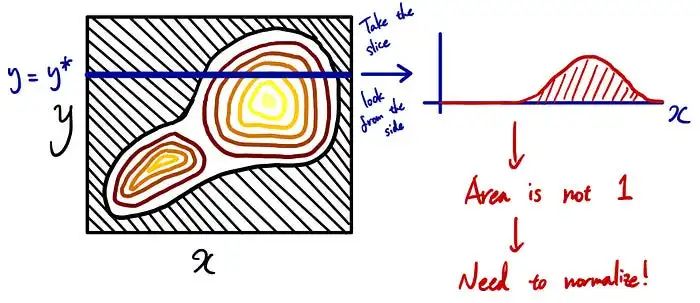
给定 y=y*,我们可以简单地从等高线图中取出切片并将其用作我们的条件概率。但是有1个问题。切片的面积不是1。为什么?还记得我之前解释的时候,这个区域所有可能的联合概率总和必须为 1 吗?这就是为什么切片不会给你 1 的原因,因为你忽略了所有其他可能的联合概率情况。因此,要使这个切片成为PDF,我们需要对面积进行归一化,使这个切片面积变为1。
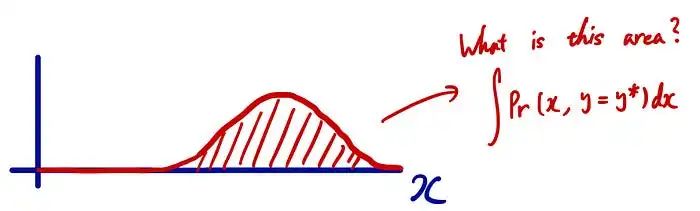
如果是连续的情况,面积用上面的积分表示。通过使用它,我们可以这样计算条件概率:
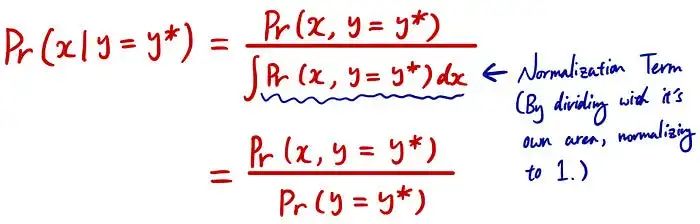
所以这就是为什么条件概率的简化形式看起来像这样:
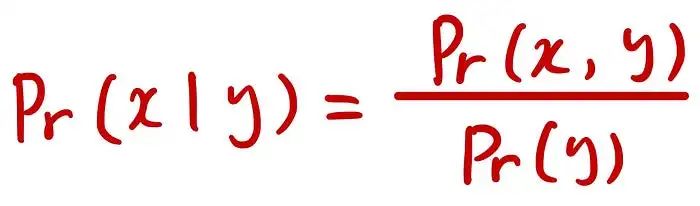
贝叶斯法则简介
今天文章的最后一个话题是另一个非常重要的概念,叫做“贝叶斯法则”。我很确定你以前听说过它。让我们仔细看看以了解这个概念。
公式本身很简单。但是这个公式是什么意思,我们如何从已知的知识中得到这个公式呢?
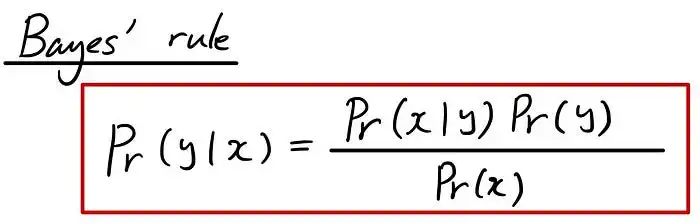
首先,让我们尝试理解公式本身。所以上面众所周知的公式可以根据我们已经学过的知识进行重写。

你不觉得这很眼熟吗?是的!这就像条件概率公式一样,我们将区域归一化为 1,以便我们可以将其视为 PDF。
因此,要分解贝叶斯定理,它是一种使用 3 个术语来计算“后验”的方法:“似然概率”、“先验”和“证据”。
后验:观察 x 后我们对 y 的了解
似然:在给定 y 的特定值的情况下观察 x 的特定值的倾向
先验:在观察 x 之前我们对 y 的了解
证据:确保左侧是有效分布的常数(归一化项)
它很有用,因为即使很难计算后验,但通常更容易根据似然、先验和证据进行计算。其他术语也是如此。
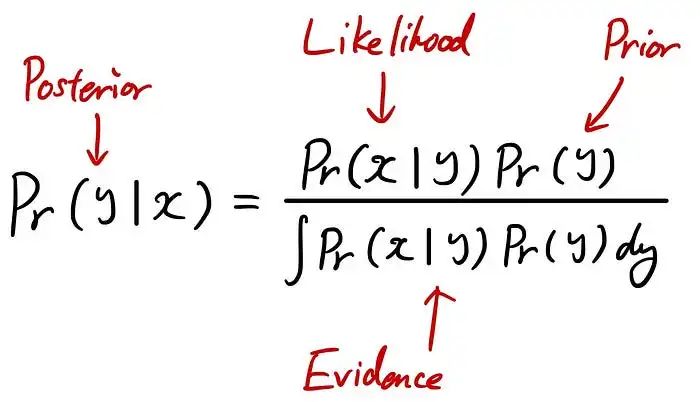
我希望你现在已经理解了这个公式。让我们看看如何从已知的知识中推导出这个公式。
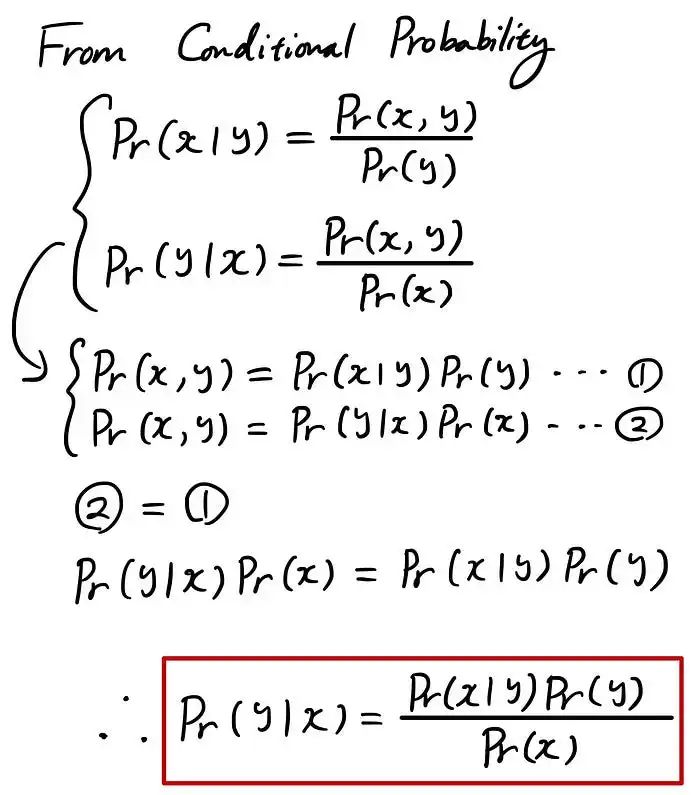
基本上,我们可以从条件概率定义中推导出贝叶斯定理。这是一个重要的概念,请务必花一些时间来理解它!
独立性简介
先说“独立”。还记得我们上次讲的联合概率吗?简而言之,联合概率是两个或多个事件同时发生的概率。如果它们是独立的,我们可以简单地将联合概率视为每个事件概率相乘。你还记得条件概率吗?一个事件的概率由其他事件决定,如果事件是独立的,则条件概率将不再受其他条件影响。它只会成为它自己的概率。

举个例子,假设您想知道 Bob 赢得网球比赛和 Amanda 赢得演讲比赛的概率。您是在与朋友打赌他们的输赢(现实生活中不要这样做!)。两项比赛在同一时间,同一天举行。根据他的统计数据,Bob 获胜的机会是 0.35 (=35%)。Amanda 的演讲非常出色,并且已经连续赢得 5 场比赛,所以我们假设它大约是 0.95 (=95%)。这些事件是独立的,因为一个事件不会影响另一个。因此,如果您押注双方都赢得比赛,则联合概率将为 0.35 * 0.95 = 0.3325 (=33.25%)。另一方面,如果您打赌 Bob 输而 Amanda 赢,则联合概率将为 (1 - 0.35) * 0.95 = 0.6175 (=61.75%)。因此,您将决定对这种组合下注……
期望简介
期望值或期望是概率和统计中最重要的基本概念之一,因此请花一些时间和精力来理解这一部分!
如果您想以简单的方式考虑,期望或期望值是简称平均值或均值。
举个简单的例子,考虑一个随机变量 X 及其对应的概率 P。期望值可以表示如下:

一般来说,期望值是随机变量和概率密度函数的所有组合的总和。
为了方便起见,我们通常使用希腊字符 μ (mu) 来书写期望值。
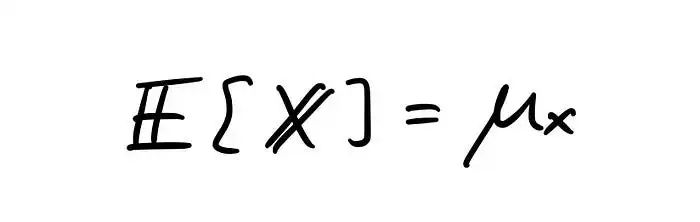
好吧,它可能还不是很清楚,所以让我给你一个具体的例子。
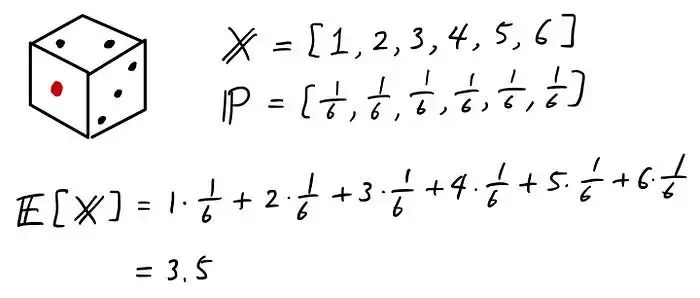
我希望你现在已经知道了期望的概念。让我们从这里看一下它们的属性。属性是概念所具有的某些规则,理解这些规则通常很有用,这样可以更容易地理解更高级的概念(比如后面的方差、协方差、偏度等)。
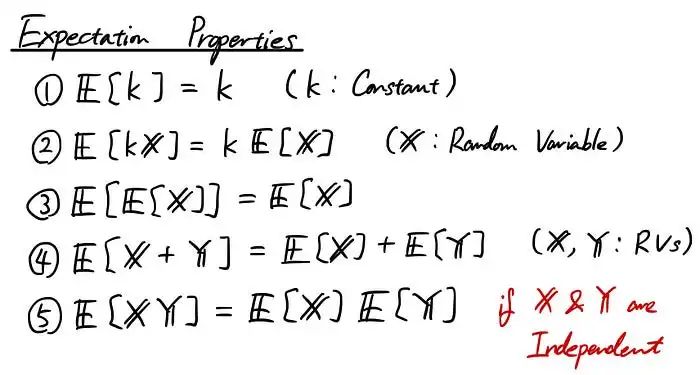
方差和协方差简介
在研究了期望之后,现在是时候进入下一个令人兴奋的话题,方差了!有时,在编写代码时将其缩写为“Var”或“var”。方差是一种度量,它告诉我们数据与均值的分布情况。该等式如下所示:
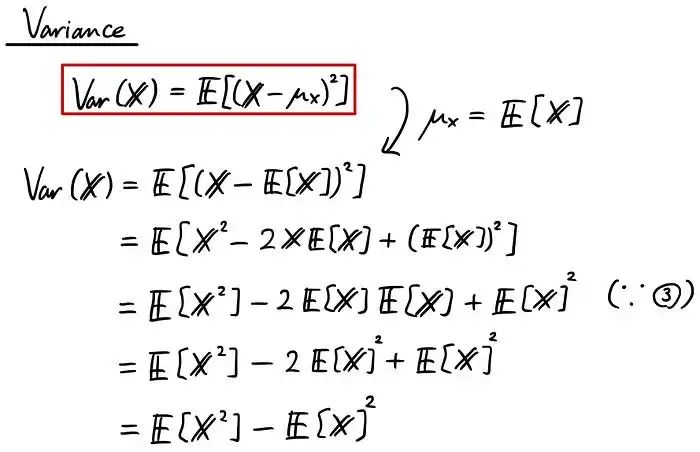
我正在使用我们学到的期望值的属性以不同的形式改变方程。我展示的第一个被红色包围的公式告诉我们,方差是从随机变量中减去均值,取平方来考虑负性,然后取期望值。
现在是“协方差”(在编写代码时通常缩写为“Cov”或“cov”)。协方差实际上是另一个非常重要的概念。每当您学习更高级的主题时,它就会不时出现。它基本上讲述了两个随机变量如何一起移动。如果一个随机变量增加其值而另一个随机变量也增加其值,则协方差很高。如果一个随机变量增加而另一个没有变化,则协方差很低。从这些词中可能很难理解,所以我先把方程式给你们看一下,让我想象一下。
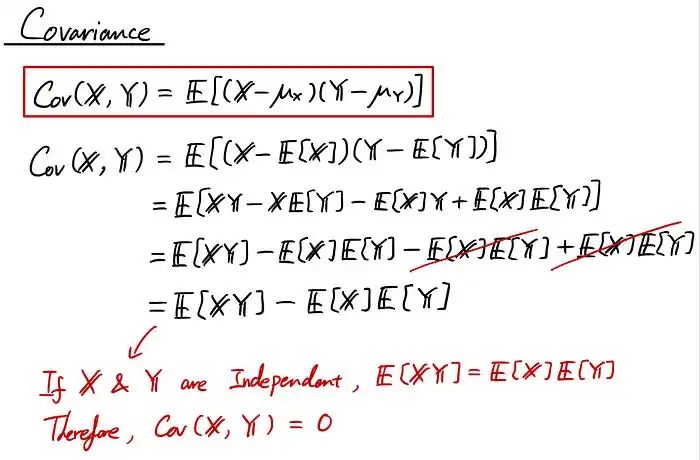
协方差的实际方程包含在红色框中。一件有趣的事情是(通过使用我们讨论的期望属性)协方差可以表示为另一种形式,如方程的第二部分,如果随机变量 X 和 Y 是独立的,则协方差为 0。
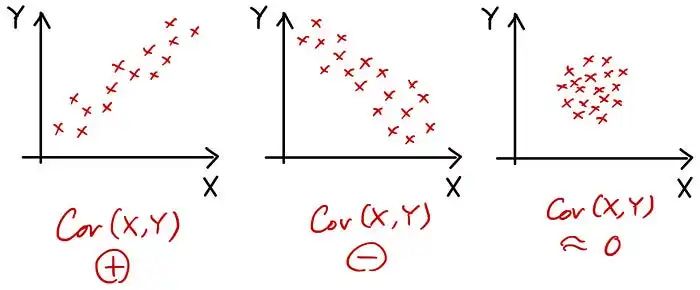
现在让我形象化协方差,以便您可以更好地了解它代表什么!
标准偏差简介
现在让我们谈谈另一个重要的统计测量,称为“标准偏差”。有时人们在编写代码时将其缩写为“Std”或“std”。标准偏差与方差非常相似,它也量化数据的变化量。在等式中,它是这样写的:
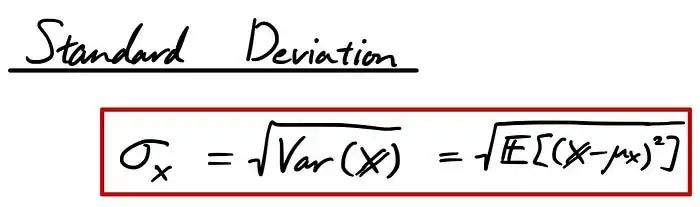
要记住的一件事是在非正态分布上使用这种测量。它仍然可以使用,但需要注意某些在处理正态分布数据时非常有用的属性此时将无法使用。例如,如果你的数据是正态分布的,1个标准差可能占数据的大约68%。2 个标准偏差几乎占据 95% 的。3 个标准偏差覆盖高达 99.7%。它通常被称为 68–95–99.7 规则。这个有用的属性只适用于正态分布。

偏度和峰度简介
与我上面解释的概念相比,您可能没有听说过“偏度”或“峰态”。但如果你真的将这些统计值视为k 阶矩,那么很明显,偏度和峰态只是另一种统计度量。

这里,“σ”是标准偏差。
首先,让我们谈谈“偏度”。简而言之,偏度是一种统计量度,它告诉我们分布是如何向右或向左倾斜的。让我给你一个形象化的例子。
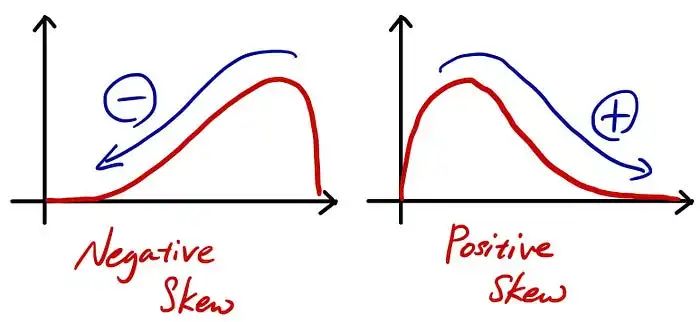
您可以通过较长的尾巴走向来记住偏度的含义。如蓝色箭头所示,如果较长的尾巴趋于负方向,则为负偏度,反之亦然。
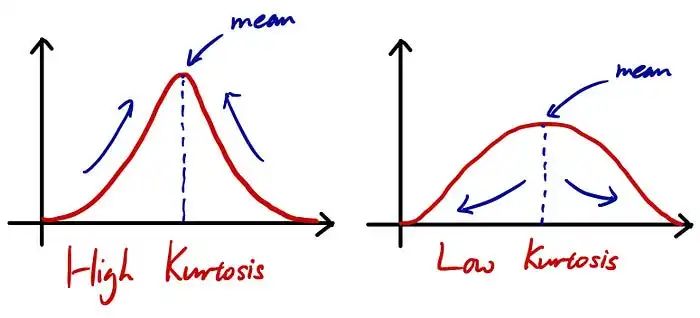
现在关于“峰度”。峰度是分布锐度的度量。峰度越高,峰值越尖锐。
总结
概率:事件发生的可能性的度量,以 0 到 1 之间的数字表示。
随机变量 (RV):就像任何其他变量一样,可用于表示随机结果的可能值的变量。
概率密度函数 (PDF):连续随机变量的密度表示为函数,其中曲线下的面积显示 RV 本身的概率。
联合概率:两个或多个随机变量同时出现的概率。
边缘化:忽略某些随机变量以获得具有较少随机变量的概率的方法。
条件概率:给定(通过假设、推定、断言或证据)另一个事件已经发生的事件的概率。
贝叶斯规则:将后验概率与似然概率、先验和证据联系起来的规则。
独立性:如果两个随机变量彼此独立,则可以将其联合概率视为其乘法。同样,如果条件概率是独立的,您可以将条件概率视为它自己的概率,而不管条件如何。
期望:最重要的统计测量。您可以将其视为使用随机变量及其相应概率取平均值。
标准偏差:用于量化您正在寻找的数据的基础分布的可变性的度量。
方差:另一种量化数据基础分布可变性的方法。
偏度:分布峰值如何向一侧(右侧或左侧)倾斜。
峰度:表示数据分布的峰值有多尖锐的度量。