策略算法
教程链接
DataWhale强化学习课程JoyRL
https://johnjim0816.com/joyrl-book/#/ch7/main
策略梯度
与前面的基于价值的算法不同,这类算法直接对策略本身进行近似优化。
在这种情况下,我们可以将策略描述成一个带有参数 θ θ θ的连续函数,该函数将某个状态作为输入,输出的不再是某个确定性的离散动作,而是对应的动作概率分布,通常用 π θ ( a ∣ s ) \pi_{θ}(a|s) πθ(a∣s) 表示,称作随机性策略。
价值算法缺点
- 无法表示连续动作
由于 DQN 等算法是通过学习状态和动作的价值函数来间接指导策略的,因此它们只能处理离散动作空间的问题,无法表示连续动作空间的问题
- 高方差
基于价值的方法通常都是通过采样的方式来估计价值函数,这样会导致估计的方差很高,从而影响算法的收敛性。尽管一些 DQN 改进算法,通过改善经验回放、目标网络等方式,可以在一定程度上减小方差,但是这些方法并不能完全解决这个问题。
- 探索与利用的平衡问题
DQN 等算法在实现时通常选择贪心的确定性策略,而很多问题的最优策略是随机策略,即需要以不同的概率选择不同的动作。虽然可以通过 ϵ -greedy \epsilon\text{-greedy} ϵ-greedy 策略等方式来实现一定程度的随机策略,但是实际上这种方式并不是很理想,因为它并不能很好地平衡探索与利用的关系。
策略梯度算法
特点: 直接对策略进行优化算法,但是优化目标与基于价值一样,都是累积的价值期望 V ∗ ( s ) V^{*}(s) V∗(s)
轨迹产生的概率:
P θ ( τ ) = p ( s 0 ) π θ ( a 0 ∣ s 0 ) p ( s 1 ∣ s 0 , a 0 ) π θ ( a 1 ∣ s 1 ) p ( s 2 ∣ s 1 , a 1 ) ⋯ = p ( s 0 ) ∏ t = 0 T π θ ( a t ∣ s t ) p ( s t + 1 ∣ s t , a t ) (9.2) \tag{9.2} \begin{aligned} P_{\theta}(\tau) &=p(s_{0}) \pi_{\theta}(a_{0} | s_{0}) p(s_{1} | s_{0}, a_{0}) \pi_{\theta}(a_{1} | s_{1}) p(s_{2} | s_{1}, a_{1}) \cdots \\ &=p(s_{0}) \prod_{t=0}^{T} \pi_{\theta}\left(a_{t} | s_{t}\right) p\left(s_{t+1} | s_{t}, a_{t}\right) \end{aligned} Pθ(τ)=p(s0)πθ(a0∣s0)p(s1∣s0,a0)πθ(a1∣s1)p(s2∣s1,a1)⋯=p(s0)t=0∏Tπθ(at∣st)p(st+1∣st,at)(9.2)
基于全期望公式得到价值的期望公式
J ( π θ ) = E τ ∼ π θ [ R ( τ ) ] = P θ ( τ 1 ) R ( τ 1 ) + P θ ( τ 2 ) R ( τ 2 ) + ⋯ = ∫ τ P θ ( τ ) R ( τ ) = E τ ∼ P θ ( τ ) [ ∑ t r ( s t , a t ) ] (9.3) \tag{9.3} \begin{aligned} J(\pi_{\theta}) = \underset{\tau \sim \pi_\theta}{E}[R(\tau)] & = P_{\theta}(\tau_{1})R(\tau_{1})+P_{\theta}(\tau_{2})R(\tau_{2})+\cdots \\ &=\int_\tau P_{\theta}(\tau) R(\tau) \\ &=E_{\tau \sim P_\theta(\tau)}[\sum_t r(s_t, a_t)] \end{aligned} J(πθ)=τ∼πθE[R(τ)]=Pθ(τ1)R(τ1)+Pθ(τ2)R(τ2)+⋯=∫τPθ(τ)R(τ)=Eτ∼Pθ(τ)[t∑r(st,at)](9.3)
由于 R ( τ ) R(\tau) R(τ)与参数 θ \theta θ无关,一来问题就稍稍简化成了如何求解 P θ ( τ ) P_{\theta}(\tau) Pθ(τ) 的梯度了
后进行一系列推导
∇ θ P θ ( τ ) = P θ ( τ ) ∇ θ P θ ( τ ) P θ ( τ ) = P θ ( τ ) ∇ θ log P θ ( τ ) (9.4) \tag{9.4} \nabla_\theta P_{\theta}(\tau)= P_{\theta}(\tau) \frac{\nabla_\theta P_{\theta}(\tau)}{P_{\theta}(\tau) }= P_{\theta}(\tau) \nabla_\theta \log P_{\theta}(\tau) ∇θPθ(τ)=Pθ(τ)Pθ(τ)∇θPθ(τ)=Pθ(τ)∇θlogPθ(τ)(9.4)
log P θ ( τ ) = log p ( s 0 ) + ∑ t = 0 T ( log π θ ( a t ∣ s t ) + log p ( s t + 1 ∣ s t , a t ) ) (9.5) \tag{9.5} \log P_{\theta}(\tau)= \log p(s_{0}) + \sum_{t=0}^T(\log \pi_{\theta}(a_t \mid s_t)+\log p(s_{t+1} \mid s_t,a_t)) logPθ(τ)=logp(s0)+t=0∑T(logπθ(at∣st)+logp(st+1∣st,at))(9.5)
∇ θ log P θ ( τ ) = ∇ θ log ρ 0 ( s 0 ) + ∑ t = 0 T ( ∇ θ log π θ ( a t ∣ s t ) + ∇ θ log p ( s t + 1 ∣ s t , a t ) ) = 0 + ∑ t = 0 T ( ∇ θ log π θ ( a t ∣ s t ) + 0 ) = ∑ t = 0 T ∇ θ log π θ ( a t ∣ s t ) (9.6) \tag{9.6} \begin{aligned} \nabla_\theta \log P_{\theta}(\tau) &=\nabla_\theta \log \rho_0\left(s_0\right)+\sum_{t=0}^T\left(\nabla_\theta \log \pi_\theta\left(a_t \mid s_t\right)+\nabla_\theta \log p\left(s_{t+1} \mid s_t, a_t\right)\right) \\ &=0+\sum_{t=0}^T\left(\nabla_\theta \log \pi_\theta\left(a_t \mid s_t\right)+0\right) \\ &=\sum_{t=0}^T \nabla_\theta \log \pi_\theta\left(a_t \mid s_t\right) \end{aligned} ∇θlogPθ(τ)=∇θlogρ0(s0)+t=0∑T(∇θlogπθ(at∣st)+∇θlogp(st+1∣st,at))=0+t=0∑T(∇θlogπθ(at∣st)+0)=t=0∑T∇θlogπθ(at∣st)(9.6)
得到目标函数的梯度
∇ θ J ( π θ ) = ∇ θ E τ ∼ π θ [ R ( τ ) ] = ∇ θ ∫ τ P θ ( τ ) R ( τ ) = ∫ τ ∇ θ P θ ( τ ) R ( τ ) = ∫ τ P θ ( τ ) ∇ θ log P θ ( τ ) R ( τ ) = E τ ∼ π θ [ ∇ θ log P θ ( τ ) R ( τ ) ] = E τ ∼ π θ [ ∑ t = 0 T ∇ θ log π θ ( a t ∣ s t ) R ( τ ) ] (9.7) \tag{9.7} \begin{aligned} \nabla_\theta J\left(\pi_\theta\right) &=\nabla_\theta \underset{\tau \sim \pi_\theta}{\mathrm{E}}[R(\tau)] \\ &=\nabla_\theta \int_\tau P_{\theta}(\tau) R(\tau) \\ &=\int_\tau \nabla_\theta P_{\theta}(\tau) R(\tau) \\ &=\int_\tau P_{\theta}(\tau) \nabla_\theta \log P_{\theta}(\tau) R(\tau) \\ &=\underset{\tau \sim \pi_\theta}{\mathrm{E}}\left[\nabla_\theta \log P_{\theta}(\tau) R(\tau)\right]\\ &= \underset{\tau \sim \pi_\theta}{\mathrm{E}}\left[\sum_{t=0}^T \nabla_\theta \log \pi_\theta\left(a_t \mid s_t\right) R(\tau)\right] \end{aligned} ∇θJ(πθ)=∇θτ∼πθE[R(τ)]=∇θ∫τPθ(τ)R(τ)=∫τ∇θPθ(τ)R(τ)=∫τPθ(τ)∇θlogPθ(τ)R(τ)=τ∼πθE[∇θlogPθ(τ)R(τ)]=τ∼πθE[t=0∑T∇θlogπθ(at∣st)R(τ)](9.7)
蒙特卡洛策略梯度算法
由于环境的初始状态为随机的,智能体的每次采样动作也是随机的,从而导致每条轨迹可能不一样。考虑采样数量足够多的轨迹,然后利用这些轨迹的平均值来近似求解目标函数的梯度。
∇ J θ ≈ 1 N ∑ n = 1 N ∑ t = 1 T n G t n ∇ log π θ ( a t n ∣ s t n ) (9.8) \tag{9.8} \nabla J_{\theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_{n}} G_{t}^{n} \nabla \log \pi_{\theta}\left(a_{t}^{n} \mid s_{t}^{n}\right) ∇Jθ≈N1n=1∑Nt=1∑TnGtn∇logπθ(atn∣stn)(9.8)
这里我们假定目标是使每回合的累积价值最大。
但是实际每回合的累积奖励或回报会受到很多因素的影响。后引入优势量来进行评估价值。
作业题
- 基于价值和基于策略的算法各有什么优缺点?
基于价值的算法的优点包括:
-
可以收敛到全局最优策略,而不是局部最优。
-
可以利用贪心策略或者epsilon-greedy策略来平衡探索和利用。
-
可以用于离散或者连续的状态空间。
基于价值的算法的缺点包括:
- 对于高维或者连续的动作空间,难以找到最优的动作。
- 需要存储和更新一个大的值函数表格或者近似函数,计算量较大。
- 不能很好地处理随机策略。
策略梯度算法优点:
- 适配连续动作空间。在将策略函数设计的时候我们已经展开过,这里不再赘述。
- 适配随机策略。由于策略梯度算法是基于策略函数的,因此可以适配随机策略,而基于价值的算法则需要一个确定的策略。此外其计算出来的策略梯度是无偏的,而基于价值的算法则是有偏的。
策略梯度算法缺点
- 采样效率低。由于使用的是蒙特卡洛估计,与基于价值算法的时序差分估计相比其采样速度必然是要慢很多的,这个问题在前面相关章节中也提到过。
- 高方差。虽然跟基于价值的算法一样都会导致高方差,但是策略梯度算法通常是在估计梯度时蒙特卡洛采样引起的高方差,这样的方差甚至比基于价值的算法还要高。
- 收敛性差。容易陷入局部最优,策略梯度方法并不保证全局最优解,因为它们可能会陷入局部最优点。策略空间可能非常复杂,存在多个局部最优点,因此算法可能会在局部最优点附近停滞。
- 难以处理高维离散动作空间:对于离散动作空间,采样的效率可能会受到限制,因为对每个动作的采样都需要计算一次策略。当动作空间非常大时,这可能会导致计算成本的急剧增加。
- 马尔可夫平稳分布需要满足什么条件?
- 非周期性:由于马尔可夫链需要收敛,那么就一定不能是周期性的,实际上我们处理的问题基本上都是非周期性的,这点不需要做过多的考虑。
- 状态连通性:即存在概率转移矩阵P,能够使得任意状态S0经过有限次转移到达状态s,反之亦然。
- REINFORCE 算法会比 Q-learning 算法训练速度更快吗?为什么?
是的。REINFORCE 算法直接优化一个参数化的策略函数,而不需要估计一个值函数.Q-learning 算法是一种基于价值的算法,它通过学习一个状态-动作值函数来评估不同动作的优劣,然后根据这个函数来选择最优的动作。
- 确定性策略与随机性策略的区别?
- 确定性策略是指在每个状态下,只选择一个固定的动作,不考虑其他可能的动作。确定性策略可以用一个函数来表示,即 a = μ ( s ) a = \mu(s) a=μ(s) ,其中 a 是动作,s 是状态, μ \mu μ是策略函数。
- 随机性策略是指在每个状态下,按照一定的概率分布来选择动作,而不是唯一确定的。随机性策略可以用一个条件概率来表示,即 π ( a ∣ s ) \pi(a|s) π(a∣s),其中 π \pi π是策略函数,表示在状态 s 下选择动作 a 的概率。
随机性策略可以更好地探索环境,避免陷入局部最优,而确定性策略可以更高效地利用已知的信息,减少计算量。
Actor-Ctitic算法
策略梯度算法优缺点:
- 适配连续动作空间。在将策略函数设计的时候我们已经展开过,这里不再赘述。
- 适配随机策略。由于策略梯度算法是基于策略函数的,因此可以适配随机策略,而基于价值的算法则需要一个确定的策略。此外其计算出来的策略梯度是无偏的,而基于价值的算法则是有偏的。
但同样的,策略梯度算法也有其缺点。
- 采样效率低。由于使用的是蒙特卡洛估计,与基于价值算法的时序差分估计相比其采样速度必然是要慢很多的,这个问题在前面相关章节中也提到过。
- 高方差。虽然跟基于价值的算法一样都会导致高方差,但是策略梯度算法通常是在估计梯度时蒙特卡洛采样引起的高方差,这样的方差甚至比基于价值的算法还要高。
- 收敛性差。容易陷入局部最优,策略梯度方法并不保证全局最优解,因为它们可能会陷入局部最优点。策略空间可能非常复杂,存在多个局部最优点,因此算法可能会在局部最优点附近停滞。
- 难以处理高维离散动作空间:对于离散动作空间,采样的效率可能会受到限制,因为对每个动作的采样都需要计算一次策略。当动作空间非常大时,这可能会导致计算成本的急剧增加。
结合策略梯度与值函数的Actor-Critic算法能够同时兼顾两者的优点,甚至还能缓解两种方法都很难解决的高方差问题。
策略梯度算法高方差来源为 直接对策略参数化,相当于既要利用策略与环境进行交互采样,又要利用采样去估计策略梯度。
价值函数算法高方差来源为 需要与环境交互采样来估计值函数。
而两者结合后,Actor网络部分还是负责估计策略梯度和采样,但是Critic网络 也就是原来的值函数部分就不需要采样只负责估计值函数,并且由于它估计的值函数为策略函数的只,相当于带来了一个更稳定的估计用于指导Actor的更新,反而能够缓解策略梯度估计带来的高方差。
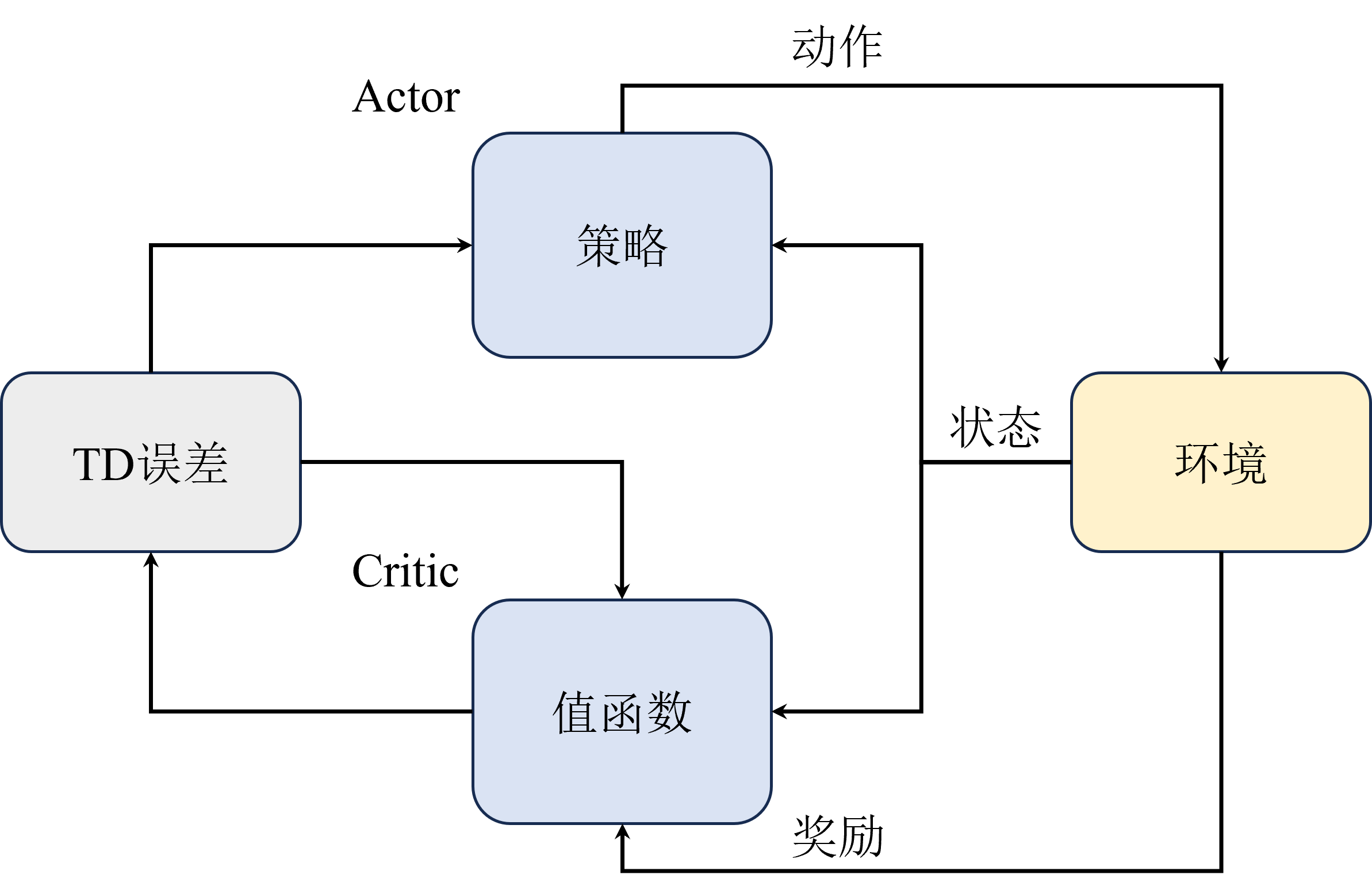
由于AC网络并不能彻底解决策略梯度算法的高方差问题,所以为了进一步缓解高方差问题,引入了一个优势函数,用来表示当前状态-动作对相当于平均水平的优势
KaTeX parse error: \tag works only in display equations
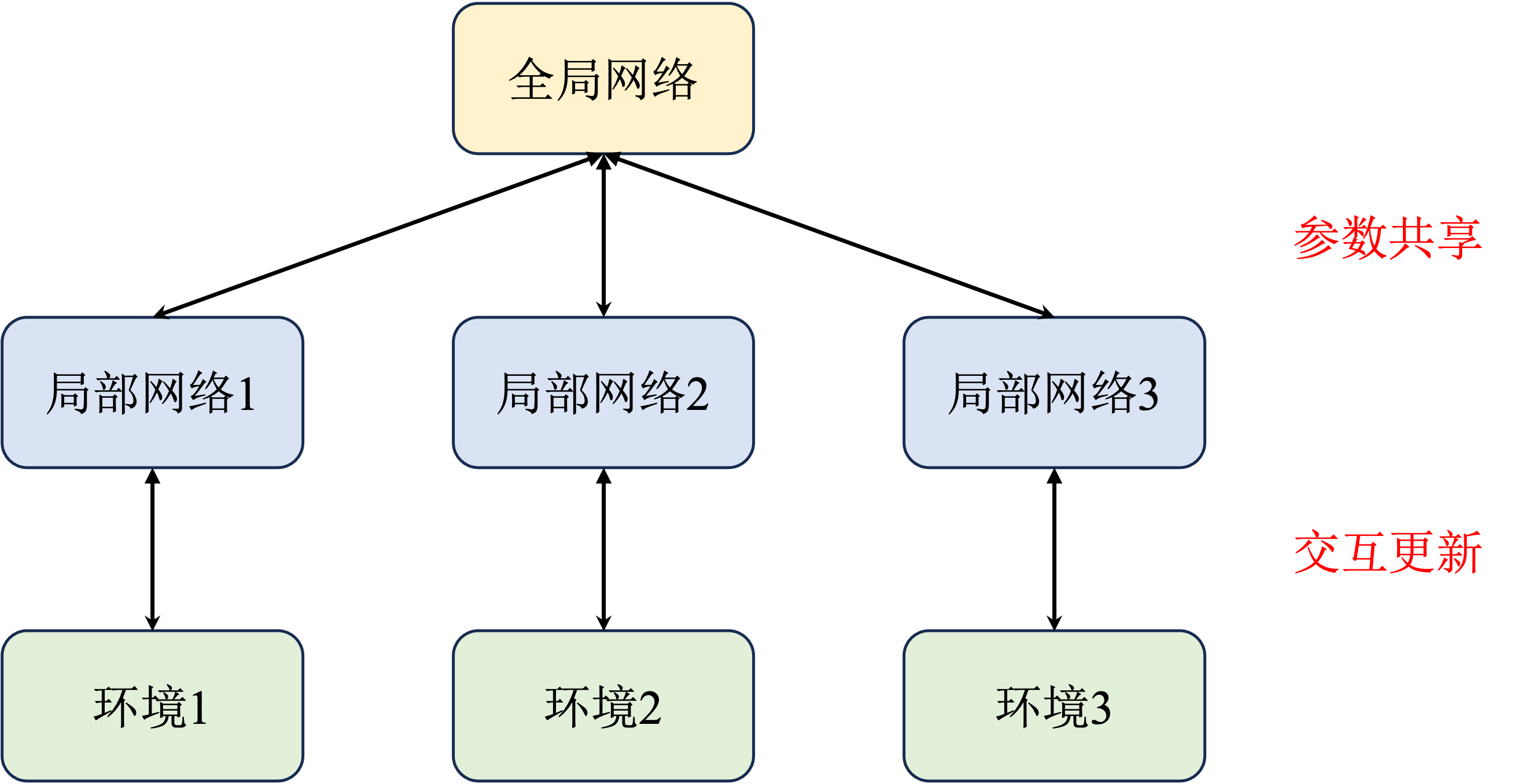
这里优势函数相当于减去了一个基线,可以自由选择,但是通常选择状态价值函数使得梯度估计更加稳定。即A2C算法。而A3C算法是在A2C基础上引入了多线程的概念提高训练效率。原先的 A2C 算法相当于只有一个全局网络并持续与环境交互更新。而 A3C 算法中增加了多个进程,每一个进程都拥有一个独立的网络和环境以供交互,并且每个进程每隔一段时间都会将自己的参数同步到全局网络中,这样就能提高训练效率。
作业题
- 相比于 REINFORCE 算法, A2C 主要的改进点在哪里,为什么能提高速度?
A2C引入了优势函数与AC演员评论家网络。A2C 算法是一种演员-评论家算法,它引入了一个值函数作为评论家,可以在每一步或者每几步就根据优势函数来更新策略和值函数。可以衡量一个动作相对于平均水平的优劣。这些改进使得 A2C 算法能够更快地收敛到最优策略,提高了训练的速度和效果。
- A2C 算法是 on-policy 的吗?为什么?
什么能提高速度?
A2C引入了优势函数与AC演员评论家网络。A2C 算法是一种演员-评论家算法,它引入了一个值函数作为评论家,可以在每一步或者每几步就根据优势函数来更新策略和值函数。可以衡量一个动作相对于平均水平的优劣。这些改进使得 A2C 算法能够更快地收敛到最优策略,提高了训练的速度和效果。
- A2C 算法是 on-policy 的吗?为什么?
是的。 A2C 算法的目标是最大化累积回报的期望,而这个期望是基于当前的策略分布的,如果使用不同的策略分布来采样数据,那么就会导致偏差和不一致。