前言

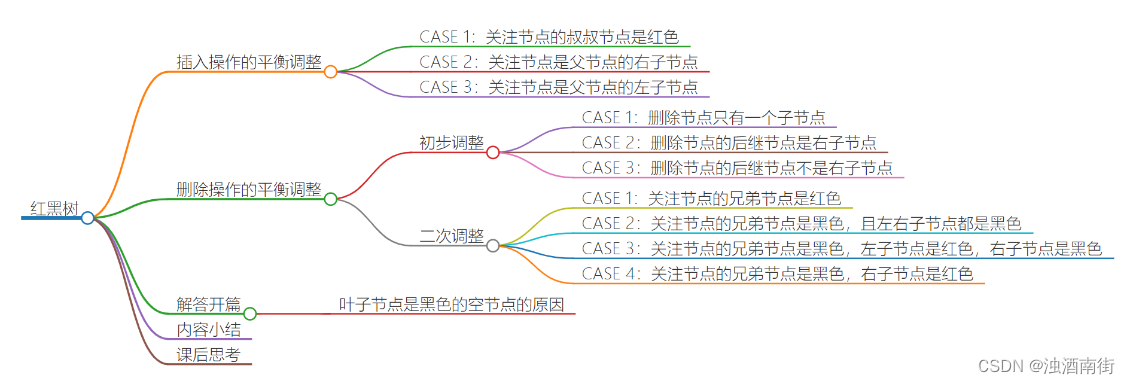
本节课程思维导图：

红黑树是一个让我又爱又恨的数据结构，“爱”是因为它稳定、高效的性能，“恨”是因为实现起来实在太难了。对于绝大部分开发工程师来说，这辈子你可能都用不着亲手写一个红黑树，所以没必要去死磕它。
上一节，我们讲到红黑树定义的时候，提到红黑树的叶子节点都是黑色的空节点。当时我只是粗略地解释了，这是为了代码实现方便，那更加确切的原因是什么呢？

实现红黑树的基本思想

实际上，红黑树的平衡过程跟魔方复原非常神似，大致过程就是：遇到什么样的节点排布，我们就对应怎么去调整。只要按照这些固定的调整规则来操作，就能将一个非平衡的红黑树调整成平衡的。

一棵合格的红黑树需要满足这样几个要求：

1. 根节点是黑色的；
2. 每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存储数据；
3. 任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的；
4. 每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点。

在插入、删除节点的过程中，第三、第四点要求可能会被破坏，而我们今天要讲的“平衡调整”，实际上就是要把被破坏的第三、第四点恢复过来。
我先介绍两个非常重要的操作，左旋（rotate left）、右旋（rotate right）。左旋全称其实是叫围绕某个节点的左旋，右旋全称其实叫围绕某个节点的右旋。我们下面的平衡调整中，会一直用到这两个操作，所以我这里画了个示意图，帮助你彻底理解这两个操作。图中的 a，b，r 表示子树，可以为空。

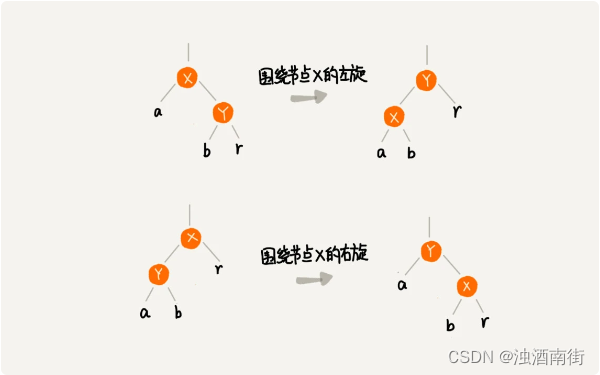
左旋是指将当前节点的右子节点旋转为当前节点的父节点，同时将当前节点作为其右子节点的左子节点。右旋是指将当前节点的左子节点旋转为当前节点的父节点，同时将当前节点作为其左子节点的右子节点。

插入操作的平衡调整

首先，我们来看插入操作。
红黑树规定，插入的节点必须是红色的。而且，二叉查找树中新插入的节点都是放在叶子节点上。所以，关于插入操作的平衡调整，有这样两种特殊情况，但是也都非常好处理。
如果插入节点的父节点是黑色的，那我们什么都不用做，它仍然满足红黑树的定义。如果插入的节点是根节点，那我们直接改变它的颜色，把它变成黑色就可以了。除此之外，其他情况都会违背红黑树的定义，于是我们就需要进行调整，调整的过程包含两种基础的操作：左右旋转和改变颜色。
红黑树的平衡调整过程是一个迭代的过程。我们把正在处理的节点叫做关注节点。关注节点会随着不停地迭代处理，而不断发生变化。最开始的关注节点就是新插入的节点。新节点插入之后，如果红黑树的平衡被打破，那一般会有下面三种情况。我们只需要根据每种情况的特点，不停地调整，就可以让红黑树继续符合定义，也就是继续保持平衡。我们下面依次来看每种情况的调整过程。提醒你注意下，为了简化描述，我把父节点的兄弟节点叫做叔叔节点，父节点的父节点叫做祖父节点。

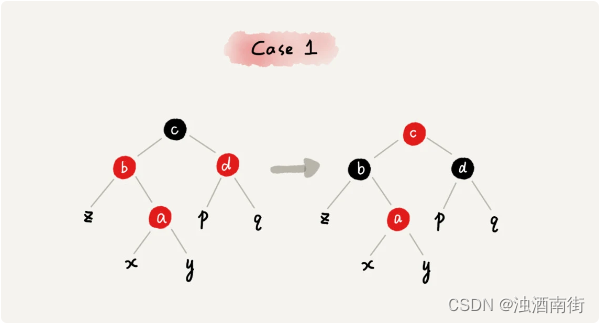
CASE 1：如果关注节点是 a，它的叔叔节点 d 是红色，我们就依次执行下面的操作：

1. 将关注节点 a 的父节点 b、叔叔节点 d 的颜色都设置成黑色；
2. 将关注节点 a 的祖父节点 c 的颜色设置成红色；
3. 关注节点变成 a 的祖父节点 c；跳到 CASE 2 或者 CASE 3。
   
   CASE 2：如果关注节点是 a，它的叔叔节点 d 是黑色，关注节点 a 是其父节点 b 的右子节点，我们就依次执行下面的操作：
4. 关注节点变成节点 a 的父节点 b；
5. 围绕新的关注节点b 左旋；
6. 跳到 CASE 3。
   
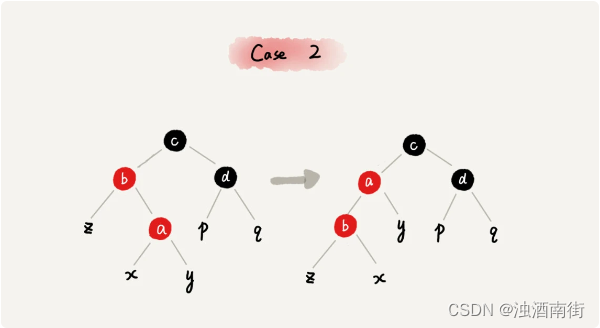
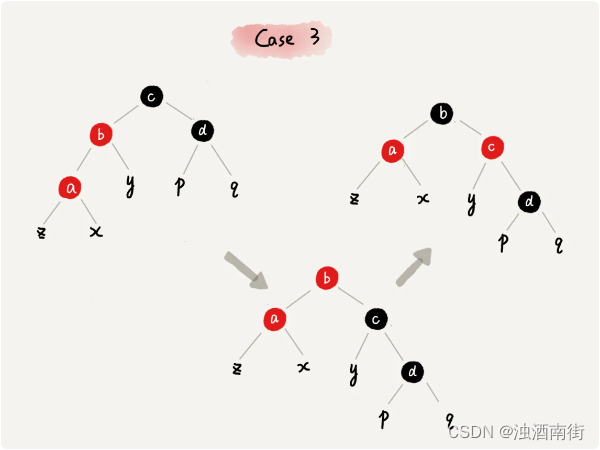
   CASE 3：如果关注节点是 a，它的叔叔节点 d 是黑色，关注节点 a 是其父节点 b 的左子节点，我们就依次执行下面的操作：
7. 围绕关注节点 a 的祖父节点 c 右旋；
8. 将关注节点 a 的父节点 b、兄弟节点 c 的颜色互换。
9. 调整结束。

删除操作的平衡调整

红黑树插入操作的平衡调整还不是很难，但是它的删除操作的平衡调整相对就要难多了。

删除操作的平衡调整分为两步，第一步是针对删除节点初步调整。初步调整只是保证整棵红黑树在一个节点删除之后，仍然满足最后一条定义的要求，也就是说，每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点；第二步是针对关注节点进行二次调整，让它满足红黑树的第三条定义，即不存在相邻的两个红色节点。

1. 针对删除节点初步调整

在下面的讲解中，如果一个节点既可以是红色，也可以是黑色，在画图的时候，我会用一半红色一半黑色来表示。如果一个节点是“红 - 黑”或者“黑 - 黑”，我会用左上角的一个小黑点来表示额外的黑色。
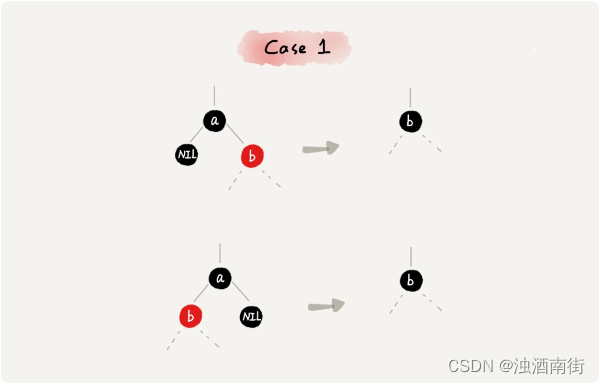
CASE 1：如果要删除的节点是 a，它只有一个子节点 b，那我们就依次进行下面的操作：
删除节点 a，并且把节点 b 替换到节点 a 的位置，这一部分操作跟普通的二叉查找树的删除操作一样；

• 节点 a 只能是黑色，节点 b 也只能是红色，其他情况均不符合红黑树的定义。
• 这种情况下，我们把节点 b 改为黑色；
• 调整结束，不需要进行二次调整。

CASE 2：如果要删除的节点 a 有两个非空子节点，并且它的后继节点就是节点 a 的右子节点 c。我们就依次进行下面的操作：
如果节点 a 的后继节点就是右子节点 c，那右子节点 c 肯定没有左子树。我们把节点 a 删除，并且将节点 c 替换到节点 a 的位置。这一部分

• 操作跟普通的二叉查找树的删除操作无异；
• 然后把节点 c 的颜色设置为跟节点 a 相同的颜色；
• 如果节点 c 是黑色，为了不违反红黑树的最后一条定义，我们给节点 c 的右子节点 d 多加一个黑色，这个时候节点 d 就成了“红 - 黑”或者“黑 - 黑”；
• 这个时候，关注节点变成了节点 d，第二步的调整操作就会针对关注节点来做。

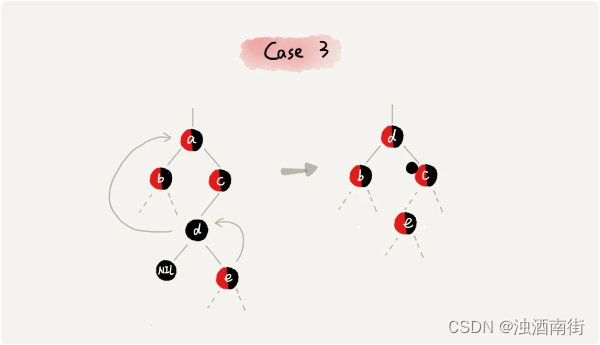
CASE 3：如果要删除的是节点 a，它有两个非空子节点，并且节点 a 的后继节点不是右子节点，我们就依次进行下面的操作：

• 找到后继节点 d，并将它删除，删除后继节点 d 的过程参照 CASE 1；
• 将节点 a 替换成后继节点 d；把节点 d 的颜色设置为跟节点 a 相同的颜色；
• 如果节点 d 是黑色，为了不违反红黑树的最后一条定义，我们给节点 d 的右子节点 c 多加一个黑色，这个时候节点 c 就成了“红 - 黑”或者“黑 - 黑”；
• 这个时候，关注节点变成了节点 c，第二步的调整操作就会针对关注节点来做。
  
• 针对关注节点进行二次调整
  经过初步调整之后，关注节点变成了“红 - 黑”或者“黑 - 黑”节点。针对这个关注节点，我们再分四种情况来进行二次调整。二次调整是为了让红黑树中不存在相邻的红色节点。
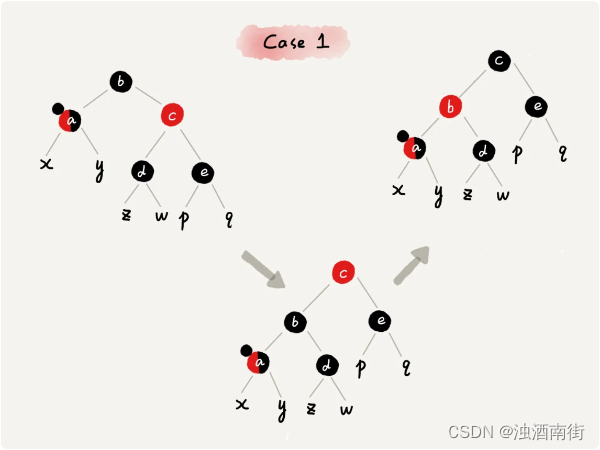
  CASE 1：如果关注节点是 a，它的兄弟节点 c 是红色的，我们就依次进行下面的操作：
• 围绕关注节点 a 的父节点 b 左旋；
• 关注节点 a 的父节点 b 和祖父节点 c 交换颜色；
• 关注节点不变；
• 继续从四种情况中选择适合的规则来调整。
  
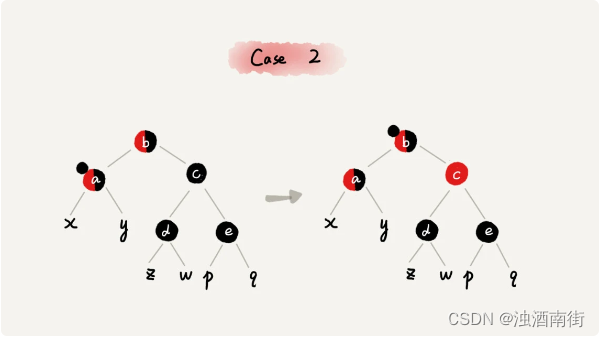
  CASE 2：如果关注节点是 a，它的兄弟节点 c 是黑色的，并且节点 c 的左右子节点 d、e 都是黑色的，我们就依次进行下面的操作：
• 将关注节点 a 的兄弟节点 c 的颜色变成红色；
• 从关注节点 a 中去掉一个黑色，这个时候节点 a 就是单纯的红色或者黑色；
• 给关注节点a 的父节点 b 添加一个黑色，这个时候节点 b 就变成了“红 - 黑”或者“黑 - 黑”；
• 关注节点从 a 变成其父节点 b；
• 继续从四种情况中选择符合的规则来调整。
  
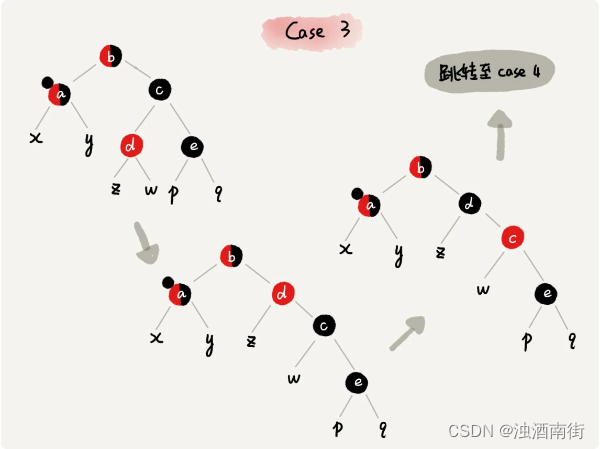
  CASE 3：如果关注节点是 a，它的兄弟节点 c 是黑色，c 的左子节点 d 是红色，c 的右子节点 e 是黑色，我们就依次进行下面的操作：
• 围绕关注节点 a 的兄弟节点 c 右旋；
• 节点 c 和节点 d 交换颜色；
• 关注节点不变；
• 跳转到 CASE 4，继续调整。

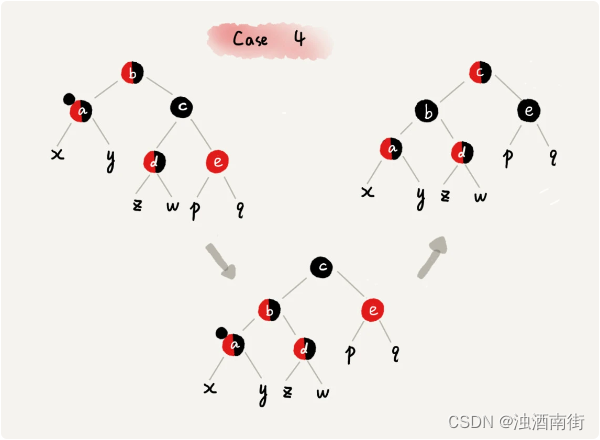
CASE 4：如果关注节点 a 的兄弟节点 c 是黑色的，并且 c 的右子节点是红色的，我们就依次进行下面的操作：

• 围绕关注节点 a 的父节点 b 左旋；
• 将关注节点 a 的兄弟节点 c 的颜色，跟关注节点 a 的父节点 b 设置成相同的颜色；
• 将关注节点 a 的父节点 b 的颜色设置为黑色；
• 从关注节点 a 中去掉一个黑色，节点 a 就变成了单纯的红色或者黑色；
• 将关注节点 a 的叔叔节点 e 设置为黑色；调整结束。
  

解答开篇

为什么红黑树的定义中，要求叶子节点是黑色的空节点？
要我说，之所以有这么奇怪的要求，其实就是为了实现起来方便。只要满足这一条要求，那在任何时刻，红黑树的平衡操作都可以归结为我们刚刚讲的那几种情况。
还是有点不好理解，我通过一个例子来解释一下。假设红黑树的定义中不包含刚刚提到的那一条“叶子节点必须是黑色的空节点”，我们往一棵红黑树中插入一个数据，新插入节点的父节点也是红色的，两个红色的节点相邻，这个时候，红黑树的定义就被破坏了。那我们应该如何调整呢？

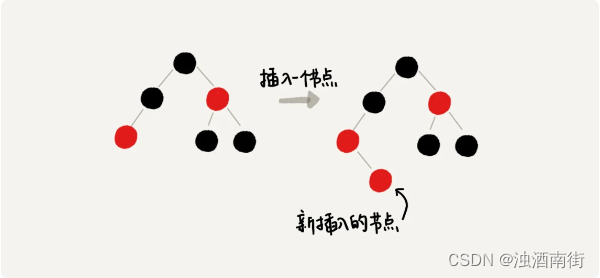
你会发现，这个时候，我们前面在讲插入时，三种情况下的平衡调整规则，没有一种是适用的。但是，如果我们把黑色的空节点都给它加上，变成下面这样，你会发现，它满足 CASE 2 了。

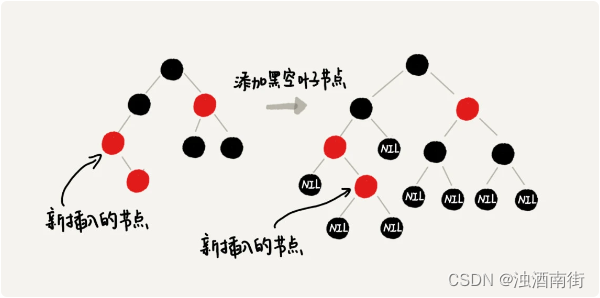
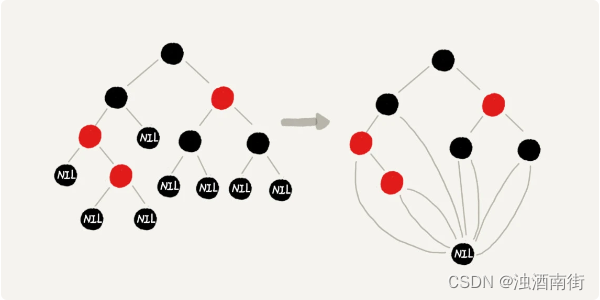
你可能会说，这样给红黑树添加黑色的空的叶子节点，会不会比较浪费存储空间呢？答案是不会的。虽然我们在讲解或者画图的时候，每个黑色的、空的叶子节点都是独立画出来的。实际上，在具体实现的时候，我们只需要像下面这样，共用一个黑色的、空的叶子节点就行了。

内容小结

现在，我就来总结一下，如何比较轻松地看懂我今天讲的操作过程。
第一点，把红黑树的平衡调整的过程比作魔方复原，不要过于深究这个算法的正确性。你只需要明白，只要按照固定的操作步骤，保持插入、删除的过程，不破坏平衡树的定义就行了。
第二点，找准关注节点，不要搞丢、搞错关注节点。因为每种操作规则，都是基于关注节点来做的，只有弄对了关注节点，才能对应到正确的操作规则中。在迭代的调整过程中，关注节点在不停地改变，所以，这个过程一定要注意，不要弄丢了关注节点。
第三点，插入操作的平衡调整比较简单，但是删除操作就比较复杂。针对删除操作，我们有两次调整，第一次是针对要删除的节点做初步调整，让调整后的红黑树继续满足第四条定义，“每个节点到可达叶子节点的路径都包含相同个数的黑色节点”。但是这个时候，第三条定义就不满足了，有可能会存在两个红色节点相邻的情况。第二次调整就是解决这个问题，让红黑树不存在相邻的红色节点。