一、什么是回归
机器学习中的回归是一种预测性分析任务,旨在找出因变量(目标变量)和自变量(预测变量)之间的关系。与分类问题不同,回归问题关注的是预测连续型或数值型数据,如温度、年龄、薪水、价格等。回归分析可以帮助我们理解当其他变量保持不变时,因变量的值如何随着自变量的变化而变化。
回归分析可以分为线性回归和非线性回归:
-
线性回归:线性回归是一种统计学方法,用于建立响应变量(通常称为y或目标)和一个或多个预测变量(称为x或特征)之间的线性关系。简单线性回归只涉及一个特征,而多元线性回归涉及多个特征。线性回归的模型可以用一次函数表示,如y = a * x + b,其中a是斜率,b是截距。
-
非线性回归:非线性回归是一种涉及非线性方程的回归分析方法,用于描述因变量和自变量之间的关系。非线性回归可以处理更复杂的关系,如指数、对数、多项式等。非线性回归模型通常通过迭代优化算法(如梯度下降)来训练。
在机器学习中,回归问题通常采用监督学习方法,即利用已标记的数据集(包含输入和目标输出)来训练模型。训练完成后,模型可以对新数据进行预测。回归分析的应用广泛,包括广告投放效果评估、房价预测、股票价格预测等。
二、什么是拟合?
拟合是一种数学方法,用于描述一组数据之间的关系。它通过在平面上的点之间绘制一条曲线来实现。拟合的方法有很多,如最小二乘法、多项式拟合等。拟合程度可以通过决定系数(也称为R²)来衡量。决定系数越接近1,表示拟合程度越好。
在机器学习和数据挖掘领域,拟合通常用于建立自变量和因变量之间的函数关系。例如,线性回归、多项式回归和非线性回归等方法都是用来拟合数据以便进行预测和分析。
三、过拟合
过拟合(overfitting)是机器学习中常见的问题,指的是模型在训练集上表现非常好,但在新样本上的泛化能力较差的现象。当模型过度拟合训练数据时,它会学习到训练数据中的噪声和细节,而无法捕捉到真正的模式和规律,导致在未见过的数据上预测性能下降。
过拟合通常是由于模型的复杂度过高或训练数据量较少造成的。以下是一些常见导致过拟合的因素:
1. 模型复杂度过高:如果模型具有过多的参数或层数,它可以过度记忆训练数据中的噪声和特殊情况,而忽略了真正的模式。过于复杂的模型可能不适合数据量较少的情况。
2. 缺乏正则化:正则化是一种用来控制模型复杂度的技术。如果在训练过程中未使用正则化方法,模型可能过度拟合训练数据。
3. 训练数据不足:当可用的训练数据较少时,模型可能难以学习到足够多的样本,并且容易过拟合已有的数据。
为了应对过拟合问题,可以采取以下策略:
1. 增加训练数据量:通过增加更多的样本,可以提供更多的信息给模型,减少过拟合的可能性。
2. 使用正则化技术:正则化方法如L1正则化、L2正则化、dropout等可以限制模型的复杂度,防止过度拟合。这些技术通过在损失函数中引入惩罚项,使得模型倾向于选择简单的解。
3. 交叉验证:使用交叉验证可以更好地评估模型的性能。通过将训练数据分成训练集和验证集,可以及时发现模型是否过拟合,并进行相应调整。
4. 特征选择:选择最具代表性的特征可以减少模型的复杂度,避免过拟合现象。可以使用特征选择算法来选择对目标变量具有最大影响力的特征。
5. 提前停止训练:在训练过程中,可以通过监控验证集上的性能指标,当性能不再提升时,提前停止训练,防止过拟合。
总之,解决过拟合问题需要综合考虑模型复杂度、数据量和正则化等因素,以找到合适的平衡点,从而提高模型在未知数据上的泛化能力。
【说人话就是,一味追求低误差,很可能导致机器为了减少误差而减少误差,即使用更加复杂的关系来拟合曲线,与实际情况脱钩。原则上解决过拟合要取得低误差与模型复杂度的平衡。】【例,本来一条直线就能解决的,一味追求最低误差,能可能变成奇形怪状的曲线】
四、欠拟合
欠拟合(underfitting)是机器学习中另一个常见的问题,指的是模型无法很好地拟合训练数据,导致在训练数据和新样本上的性能都较差。当模型过于简单或不足够强大时,往往无法捕捉到数据中的复杂模式和规律,从而导致欠拟合现象。
以下是一些常见导致欠拟合的因素:
-
模型复杂度过低:如果模型的容量不足以表示数据中的关键特征和模式,模型会很难适应训练数据,并且无法提供准确的预测结果。
-
特征选择不足:选择的特征可能不足以描述数据的复杂性,或者特征之间的关系没有充分考虑。这会导致模型无法捕捉到数据中潜在的规律。
-
训练数据噪声过多:如果训练数据中存在较多的噪声或异常值,模型可能过于敏感地学习到这些不相关的信息,从而影响了其泛化能力。
为了解决欠拟合问题,可以采取以下策略:
-
增加模型复杂度:通过增加模型的参数或层数,可以提高模型的拟合能力。但需要注意避免过拟合,可以使用正则化等方法进行控制。
-
增加特征数量和多样性:添加更多合适的特征,并考虑不同特征之间的组合关系,可以提供更多信息给模型,提高其表达能力。
-
数据预处理:对训练数据进行必要的预处理,如去除异常值、平衡样本分布、缩放特征等,可以减少噪声对模型的影响,帮助模型更好地拟合数据。
-
调整超参数:通过调整模型的超参数,如学习率、正则化项的权重等,可以寻找到更适合数据的模型配置,提高拟合能力。
-
使用更复杂的模型:如果简单模型无法很好地拟合数据,可以尝试更复杂的模型,如深度神经网络、支持向量机等,以提高模型的非线性拟合能力。

五、回归的准确性判断
1.平均绝对误差(Mean Absolute Error,MAE):所有数据点绝对误差的平均值。
计算公式如下:
MAE = (1/n) * ∑(|y_i - ŷ_i|)
其中,n为样本数量,y_i为实际值,ŷ_i为预测值。
平均绝对误差越小,表示预测值与实际值之间的差异越小,模型的准确性越高。MAE常用于回归分析、时间序列预测等领域。与均方误差(MSE)和均方根误差(RMSE)相比,MAE对异常值的影响较小,因此在评估模型准确性时具有更好的稳定性。
2.均方误差(Mean Squared Error,简称MSE)是一种衡量预测值与实际值之间差异的指标。它是指预测值与实际值之差的平方值的平均值。MSE可以用于评估模型或预测方法的准确性。
计算公式如下:
MSE = (1/n) * ∑(y_i - ŷ_i)^2
其中,n为样本数量,y_i为实际值,ŷ_i为预测值。
均方误差越小,表示预测值与实际值之间的差异越小,模型的准确性越高。MSE广泛应用于回归分析、时间序列预测等领域。然而,MSE对异常值的影响较大,因此在评估模型准确性时可能不够稳定。与平均绝对误差(MAE)和均方根误差(RMSE)相比,MSE在评价模型准确性时可能不够敏感。
3.中位数绝对误差(Median Absolute Error,简称MAE)是一种衡量预测值与实际值之间差异的指标。它是指预测值与实际值之差的绝对值的 median(中位数)。MAE可以用于评估模型或预测方法的准确性。
计算公式如下:
MAE = median(|y_i - ŷ_i|)
其中,y_i为实际值,ŷ_i为预测值。
与均方误差(MSE)和均方根误差(RMSE)相比,中位数绝对误差具有以下优点:
- 对异常值不敏感,稳定性较高。
- 更容易理解和解释。
4.解释方差分
方差分(Variance Fraction,简称VF)是一种用于评估数据集内在结构特征的统计量。它反映了数据集中不同方差等级(或称不同频率)的信息含量。方差分可用于分析信号、图像等数据的特性,并为信号处理、数据压缩等领域提供依据。
方差分的计算公式如下:
VF = (var(X) - var(Y)) / var(X)
其中,X表示原始数据集,Y表示经过滤波处理后的数据集。var(X)和var(Y)分别表示X和Y的方差。
方差分(VF)的取值范围为[0, 1]。当VF接近1时,说明数据集的高频成分较多,噪声较大;当VF接近0时,说明数据集的低频成分较多,噪声较小。通过分析方差分,可以了解数据的内在结构特征以及滤波效果的好坏。
在实际应用中,方差分(VF)常用于评估滤波器性能、信号处理算法等方面的性能。通过比较不同算法的方差分,可以优选滤波器参数,提高信号处理效果。此外,方差分还可以应用于医学影像处理、语音信号处理等领域,以提取有效信息、消除噪声干扰。
5.相关系数(Correlation Coefficient)是一种用于衡量两个变量之间线性关系强度的统计量。它的值介于-1和1之间,表示两个变量之间的线性相关程度。相关系数的计算公式如下:
ρ(X,Y)= cov(X,Y)/ (σX * σY)
其中,X和Y是两个随机变量,cov(X,Y)表示它们的协方差,σX和σY分别表示它们的标准差。
相关系数具有以下性质:
1. 当ρ(X,Y)= 1时,表示X和Y完全正相关;
2. 当ρ(X,Y)= -1时,表示X和Y完全负相关;
3. 当ρ(X,Y)= 0时,表示X和Y之间不存在线性关系,但可能存在其他类型的关系(如非线性关系);
4. 当0 < ρ(X,Y)< 1时,表示X和Y存在正线性关系,但相关程度较低;
5. 当-1 < ρ(X,Y)< 0时,表示X和Y存在负线性关系,但相关程度较低。
相关系数在实际应用中广泛应用于经济学、金融学、统计学、社会科学等领域。通过计算相关系数,可以分析变量之间的关联性,为建模、预测和决策提供依据。然而,需要注意的是,相关系数仅能反映线性关系,对于非线性关系,相关系数可能会产生误导。因此,在实际分析中,还需结合其他方法(如回归分析、协方差分析等)以获得更全面的结果。
6.决定系数(R²)在统计学中是一个重要概念,用于衡量自变量对因变量的解释程度。决定系数 ranges 从 0 到 1,其中:
-
R² = 0:表示自变量对因变量没有解释力度,即两个变量之间不存在线性关系; -
R² = 1:表示自变量完全解释了因变量的变异,即两个变量之间存在完美的线性关系。
在实际应用中,决定系数 R² 可以用于评估回归模型(如线性回归、逻辑回归等)的拟合效果。较高的 R² 值表示模型能够较好地解释因变量的变异,较低的 R² 值则表示模型拟合效果不佳,需要进一步优化。
计算决定系数 R² 的公式如下:
R² = 1 - (SSR² / SSE²)
其中:
-
SSR:回归平方和,表示自变量对因变量的贡献; -
SSE:残差平方和,表示自变量无法解释的因变量变异。
【即:1-∑(预测值-实际值)^2/预测值^2,本质是利用了最小二乘法实现】
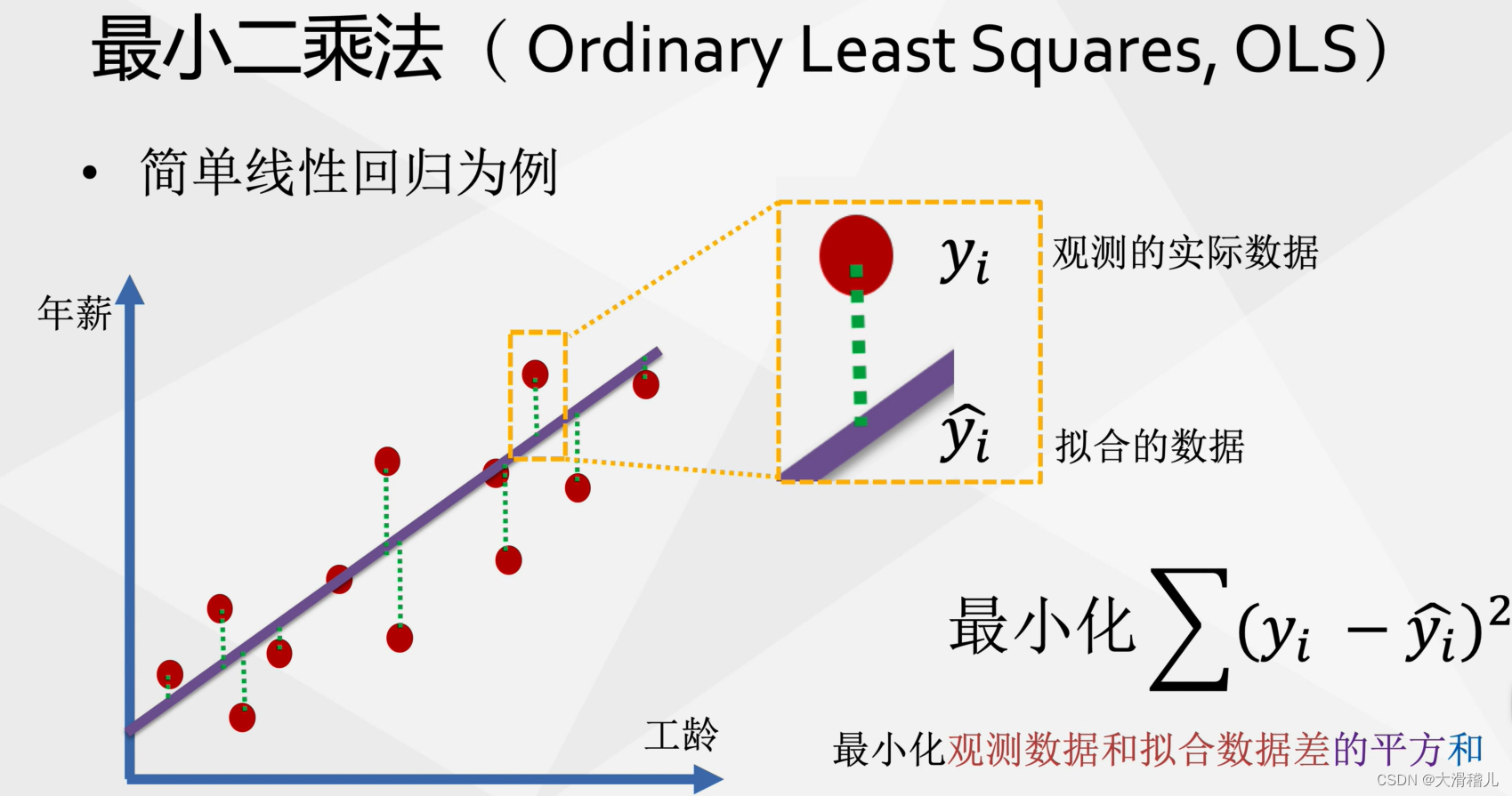
决定系数 R² 越高,表明自变量对因变量的解释力度越强,模型拟合效果越好。在实际分析中,我们可以根据 R² 值来选择最优的模型,提高预测精度。同时,R² 值还可以用于比较不同模型之间的拟合效果,选取最佳模型。
需要注意的是,决定系数 R² 仅衡量自变量对因变量的线性关系,未能考虑非线性关系。在实际应用中,我们还可以使用其他指标(如均方根误差、决定系数等)来评估模型的拟合效果,以选取最优模型。
最小二乘法(Least Squares Method)是一种数学优化技术,用于通过最小化误差的平方和来寻找最佳拟合函数。它在各个领域有广泛的应用,如线性回归、曲线拟合、信号处理等。最小二乘法的基本原理是寻找一条直线或曲线,使得所有数据点到这条直线的垂直距离之和最小。