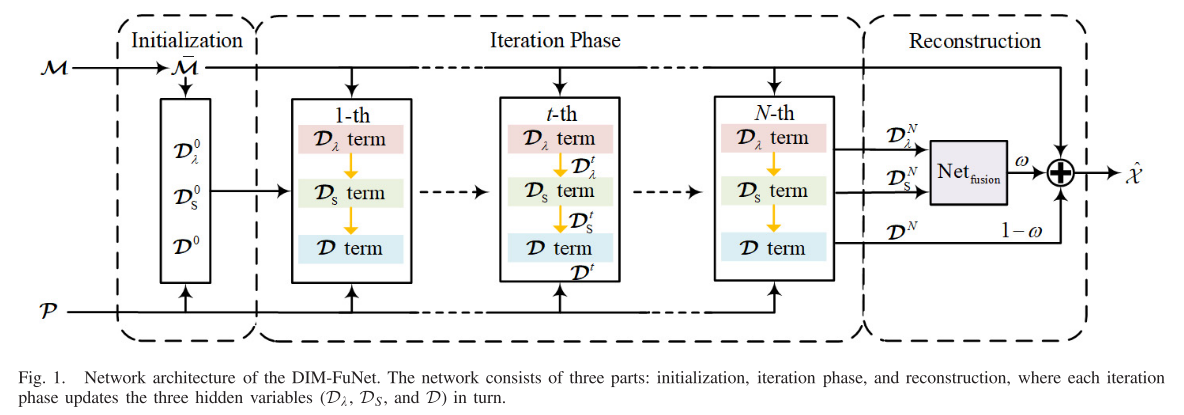
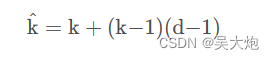今日主要总结一下动态规划的一道题目,剑指 Offer 46. 把数字翻译成字符串
题目:剑指 Offer 46. 把数字翻译成字符串
Leetcode题目地址
题目描述:
给定一个数字,我们按照如下规则把它翻译为字符串:0 翻译成 “a” ,1 翻译成 “b”,……,11 翻译成 “l”,……,25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数,用来计算一个数字有多少种不同的翻译方法。
示例 1:
输入: 12258
输出: 5
解释: 12258有5种不同的翻译,分别是"bccfi", “bwfi”, “bczi”, “mcfi"和"mzi”
提示:
0 <= num < 2^31
本题重难点
首先我们来通过一个例子理解一下这里「翻译」的过程:我们来尝试翻译「1402」。
分成两种情况:
- 首先我们可以把每一位单独翻译,即 [1, 4, 0, 2],翻译的结果是 beac
- 然后我们考虑组合某些连续的两位:
- [14, 0, 2],翻译的结果是 oac。
- [1, 40, 2],这种情况是不合法的,因为 40 不能翻译成任何字母。
- [1, 4, 02],这种情况也是不合法的,含有前导零的两位数不在题目规定的翻译规则中,那么 [14, 02]显然也是不合法的。
那么我们可以归纳出翻译的规则,字符串的第 i 位置:
- 可以单独作为一位来翻译
- 如果第 i - 1 位和第 i 位组成的数字在 10 到 25 之间,可以把这两位连起来翻译
我们可以用 f(i) 表示以第 i 位结尾的前缀串翻译的方案数,考虑第 i 位单独翻译和与前一位连接起来再翻译对 f(i) 的贡献。单独翻译对 f(i)的贡献为 f(i - 1));如果第 i - 1位存在,并且第 i - 1位和第 i 位形成的数字 x 满足10 ≤ x ≤ 25,那么就可以把第 i - 1 位和第 i 位连起来一起翻译,对 f(i) 的贡献为 f(i−2),否则为 0。我们可以列出这样的动态规划转移方程:
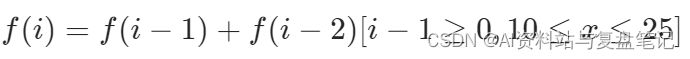
这里其实可以类比成青蛙跳台阶问题,跳一步是恒成立的,因为每个数字都会对应一个字母。能否跳两步呢?即青蛙所在的数字和下一个数字能否在10~25之间,如果可以,青蛙就跳两步。
动规五部曲分析如下:
-
确定dp数组(dp table)以及下标的含义:
dp[i]代表以 nums[i] 为结尾的数字的翻译方案数量 -
确定递推公式
若 nums[i - 1] 和 nums[i - 2] 组成的两位数字可以被翻译,则 dp[i] = dp[i - 1] + dp[i - 2];否则 dp[i] = dp[i - 1]

-
dp数组如何初始化
dp[0]=dp[1]=1 ,即 “无数字” 和 “第 1 位数字” 的翻译方法数量均为 11; -
确定遍历顺序
因为递推公式含有 dp[i - 2], i - 2 > 0 ,所以 i 从 2开始正序遍历 -
有问题时别忘了打印dp数组
C++代码
class Solution {
public:
int translateNum(int num) {
if(num < 10) return 1;
string s = to_string(num);
vector<int>dp(s.size() + 1, 0);
dp[0] = 1;
dp[1] = 1;
for(int i = 2; i <= s.size(); i++){
if(s[i - 2] == '1' || (s[i - 2] == '2' && s[i - 1] <= '5')){
dp[i] = dp[i - 1] + dp[i - 2];
}
else{
dp[i] = dp[i - 1];
}
}
return dp[s.size()];
}
};
总结
动态规划
英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。
动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的
对于动态规划问题,可以拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
这篇文章主要总结了使用动态规划解决剑指 Offer 46. 把数字翻译成字符串问题,依然是使用动规五部曲,做每道动态规划题目这五步都要弄清楚才能更清楚的理解题目!
欢迎大家关注本人公众号:编程复盘与思考随笔
(关注后可以免费获得本人在csdn发布的资源源码)