目录
语法
说明
示例
矩阵的随机列
两个随机变量
矩阵的 P 值
相关性边界
NaN 值
corrcoef函数的功能是返回数据的相关系数。
语法
R = corrcoef(A)
R = corrcoef(A,B)
[R,P] = corrcoef(___)
[R,P,RL,RU] = corrcoef(___)
___ = corrcoef(___,Name,Value)说明
R = corrcoef(A) 返回 A 的相关系数的矩阵,其中 A 的列表示随机变量,行表示观测值。
R = corrcoef(A,B) 返回两个随机变量 A 和 B 之间的系数。
[R,P] = corrcoef(___) 返回相关系数的矩阵和 p 值矩阵,用于测试观测到的现象之间没有关系的假设(原假设)。此语法可与上述语法中的任何参数结合使用。如果 P 的非对角线元素小于显著性水平(默认值为 0.05),则 R 中的相应相关性被视为显著。如果 R 包含复数元素,则此语法无效。
[R,P,RL,RU] = corrcoef(___) 包括矩阵,这些矩阵包含每个系数的 95% 置信区间的下界和上界。如果 R 包含复数元素,则此语法无效。
___ = corrcoef(___,Name,Value) 在上述语法的基础上,通过一个或多个 Name,Value 对组参数指定其他选项以返回任意输出参数。例如,corrcoef(A,'Alpha',0.1) 指定 90% 置信区间,corrcoef(A,'Rows','complete') 省略 A 的包含一个或多个 NaN 值的所有行。
示例
矩阵的随机列
计算一个矩阵的相关系数,该矩阵具有两个正态分布的随机列,其中一个列依据另一个列来定义。由于 A 的第三个列是第二个列的倍数,这两个变量直接相关,因此 R 的 (2,3) 和 (3,2) 元的相关系数为 1。
x = randn(6,1);
y = randn(6,1);
A = [x y 2*y+3];
R = corrcoef(A)
R = 3×3
1.0000 -0.6237 -0.6237
-0.6237 1.0000 1.0000
-0.6237 1.0000 1.0000两个随机变量
计算两个正态分布的随机向量(其中每个包含 10 个观测值)之间的相关系数矩阵。
A = randn(10,1);
B = randn(10,1);
R = corrcoef(A,B)
R = 2×2
1.0000 0.4518
0.4518 1.0000矩阵的 P 值
计算一个正态分布的随机矩阵的相关系数和 p 值,其中添加的第四列等于其他三列之和。由于 A 的最后一列是其他列的线性组合,第四个变量与其他三个变量中的每一个之间建立了相关性。因此,P 的第四行和第四列包含非常小的 p 值,将其标识为显著相关。
A = randn(50,3);
A(:,4) = sum(A,2);
[R,P] = corrcoef(A)
R = 4×4
1.0000 0.1135 0.0879 0.7314
0.1135 1.0000 -0.1451 0.5082
0.0879 -0.1451 1.0000 0.5199
0.7314 0.5082 0.5199 1.0000
P = 4×4
1.0000 0.4325 0.5438 0.0000
0.4325 1.0000 0.3146 0.0002
0.5438 0.3146 1.0000 0.0001
0.0000 0.0002 0.0001 1.0000相关性边界
创建一个正态分布的随机矩阵,其中添加的第四列等于其他三列之和,并计算相关系数、p 值以及系数的下界和上界。
A = randn(50,3);
A(:,4) = sum(A,2);
[R,P,RL,RU] = corrcoef(A)
R = 4×4
1.0000 0.1135 0.0879 0.7314
0.1135 1.0000 -0.1451 0.5082
0.0879 -0.1451 1.0000 0.5199
0.7314 0.5082 0.5199 1.0000
P = 4×4
1.0000 0.4325 0.5438 0.0000
0.4325 1.0000 0.3146 0.0002
0.5438 0.3146 1.0000 0.0001
0.0000 0.0002 0.0001 1.0000
RL = 4×4
1.0000 -0.1702 -0.1952 0.5688
-0.1702 1.0000 -0.4070 0.2677
-0.1952 -0.4070 1.0000 0.2825
0.5688 0.2677 0.2825 1.0000
RU = 4×4
1.0000 0.3799 0.3575 0.8389
0.3799 1.0000 0.1388 0.6890
0.3575 0.1388 1.0000 0.6974
0.8389 0.6890 0.6974 1.0000
默认情况下,矩阵 RL 和 RU 根据 95% 置信区间分别给出每个相关系数的下界和上界。可以通过指定 Alpha 的值来更改置信水平,该值定义百分比置信度 100*(1-Alpha)%。例如,使用 Alpha 值 0.01 来计算 99% 置信区间,这将反映在 RL 和 RU 边界中。99% 置信度的 RL 和 RU 中的系数边界定义的区间大于 95% 置信度所定义的区间,因为置信度越高,需要的可能相关性值范围越大。
[R,P,RL,RU] = corrcoef(A,'Alpha',0.01)
R = 4×4
1.0000 0.1135 0.0879 0.7314
0.1135 1.0000 -0.1451 0.5082
0.0879 -0.1451 1.0000 0.5199
0.7314 0.5082 0.5199 1.0000
P = 4×4
1.0000 0.4325 0.5438 0.0000
0.4325 1.0000 0.3146 0.0002
0.5438 0.3146 1.0000 0.0001
0.0000 0.0002 0.0001 1.0000
RL = 4×4
1.0000 -0.2559 -0.2799 0.5049
-0.2559 1.0000 -0.4792 0.1825
-0.2799 -0.4792 1.0000 0.1979
0.5049 0.1825 0.1979 1.0000
RU = 4×4
1.0000 0.4540 0.4332 0.8636
0.4540 1.0000 0.2256 0.7334
0.4332 0.2256 1.0000 0.7407
0.8636 0.7334 0.7407 1.0000
NaN 值
创建一个包括 NaN 值的正态分布矩阵,并计算相关系数矩阵,但排除包含 NaN 的任何行。
A = randn(5,3);
A(1,3) = NaN;
A(3,2) = NaN;
A
A = 5×3
0.5377 -1.3077 NaN
1.8339 -0.4336 3.0349
-2.2588 NaN 0.7254
0.8622 3.5784 -0.0631
0.3188 2.7694 0.7147
R = corrcoef(A,'Rows','complete')
R = 3×3
1.0000 -0.8506 0.8222
-0.8506 1.0000 -0.9987
0.8222 -0.9987 1.0000
使用 'all' 以在计算中包含所有 NaN 值。
R = corrcoef(A,'Rows','all')
R = 3×3
1 NaN NaN
NaN NaN NaN
NaN NaN NaN
使用 'pairwise' 以在成对基础上计算每个两列相关系数。如果两列中的一列包含一个 NaN,该行将被忽略。
R = corrcoef(A,'Rows','pairwise')
R = 3×3
1.0000 -0.3388 0.4649
-0.3388 1.0000 -0.9987
0.4649 -0.9987 1.0000
参数说明
A — 输入数组
输入数组,指定为矩阵。
-
如果 A 是标量,则 corrcoef(A) 返回 NaN。
-
如果 A 是向量,则 corrcoef(A) 返回 1。
B — 其他输入数组
其他输入数组,指定为向量、矩阵或多维数组。
-
A 和 B 的大小必须相同。
-
如果 A 和 B 是标量,则 corrcoef(A,B) 返回 1。然而,如果 A 和 B 相等,则 corrcoef(A,B) 返回 NaN。
-
如果 A 和 B 是矩阵或多维数组,则 corrcoef(A,B) 将每个输入转换为其向量表示形式,等效于 corrcoef(A(:),B(:)) 或 corrcoef([A(:) B(:)])。
-
如果 A 和 B 是 0×0 空数组,corrcoef(A,B) 返回一个 NaN 值的 2×2 矩阵。
名称-值参数
将可选的参数对组指定为 Name1=Value1,...,NameN=ValueN,其中 Name 是参数名称,Value 是对应的值。名称-值参数必须出现在其他参数之后,但参数对组的顺序无关紧要。
在 R2021a 之前,使用逗号分隔每个名称和值,并用引号将 Name 引起来。
Alpha — 显著性水平
显著性水平,指定为一个 0 到 1 之间的数值。'Alpha' 参数的值为相关系数定义百分比置信水平,即 100*(1-Alpha)%,用来确定 RL 和 RU 中的边界。
Rows — 使用 NaN 选项
使用 NaN 选项,指定为下列值之一:
-
'all' - 计算相关系数时将输入中的所有 NaN 值纳入在内。
-
'complete' - 计算相关系数时忽略输入中任何包含 NaN 值的行。此选项始终返回一个半正定矩阵。
-
'pairwise' - 对于每个两列相关系数计算,忽略任何仅包含成对 NaN 的行。此选项可返回非半正定矩阵。
R— 相关系数
相关系数,以矩阵形式返回。
-
对于单矩阵输入,根据 A 表示的随机变量数(列数),R 的大小为 [size(A,2) size(A,2)]。对角线元素按照约定设置为 1,而非对角线元素是变量对组的相关系数。系数值的范围是从 -1 到 1,其中 -1 表示直接负相关性,0 表示无相关性,1 表示直接正相关性。R 是对称的。
-
对于两个输入参数,R 是 2×2 矩阵,其中对角线元素为 1,非对角线元素为相关系数。
-
如果任何随机变量为常量,则它与所有其他变量的相关性为未定义,且各自的行和列值为 NaN。
P — P 值
P 值,以矩阵形式返回。P 是对称的,且大小与 R 相同。对角线元素全部为 1,非对角线元素是每个变量对组的 p 值。P 值的范围是从 0 到 1,其中接近 0 的值对应于 R 中的显著相关性,表示观测到原假设情况的概率较低。
RL — 相关系数的下界
相关系数的下界,以矩阵形式返回。RL 是对称的,且大小与 R 相同。对角线元素全部为 1,非对角线元素是 R 中相应系数的 95% 置信区间下界。如果 R 包含复数值,则返回 RL 的语法无效。
RU — 相关系数的上界
相关系数的上界,以矩阵形式返回。RU 是对称的,且大小与 R 相同。对角线元素全部为 1,非对角线元素是 R 中相应系数的 95% 置信区间上界。如果 R 包含复数值,则返回 RL 的语法无效。
相关系数
两个随机变量的相关系数用于度量其线性相关性。如果每个变量具有 N 个标量观测值,则 Pearson 相关系数定义为
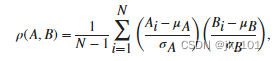
,其中 μA 和 σA 分别是 A 的均值和标准差,μB 和 σB 是 B 的均值和标准差。也可以根据 A 和 B 的协方差定义相关系数:
![]()
两个随机变量的相关系数矩阵是每个对组变量组合的相关系数的矩阵,
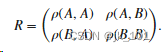
由于 A 和 B 始终直接与自身相关,对角线上的元素均为 1,即,
![]()