1 激活函数介绍
1.1 什么是激活函数
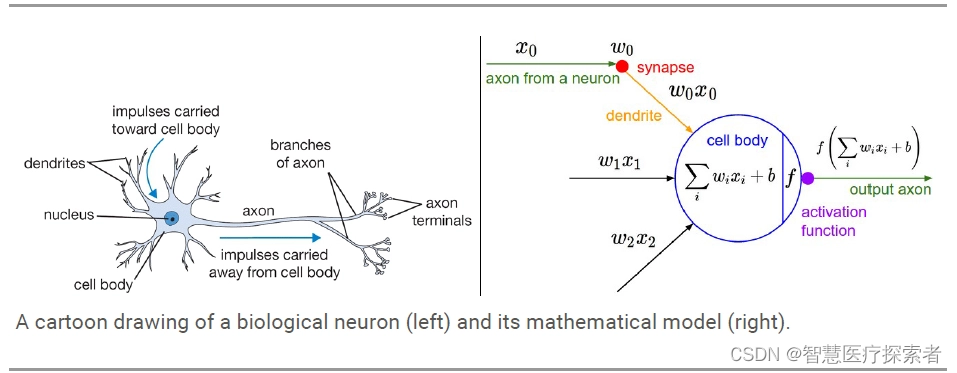
激活函数是神经网络中引入的非线性函数,用于捕获数据中的复杂关系。它来自动物界的灵感,动物的神经元会接受来自对它有作用的其他神经元的信号,当然这些信号对该神经元的作用大小不同(即具有不同的权重)。那么该神经元的信号值就是其他神经元信号加权求和后的值。如果该信号值大于指定阈值,则会激活,否则不会激活,抽象的数学模型为:
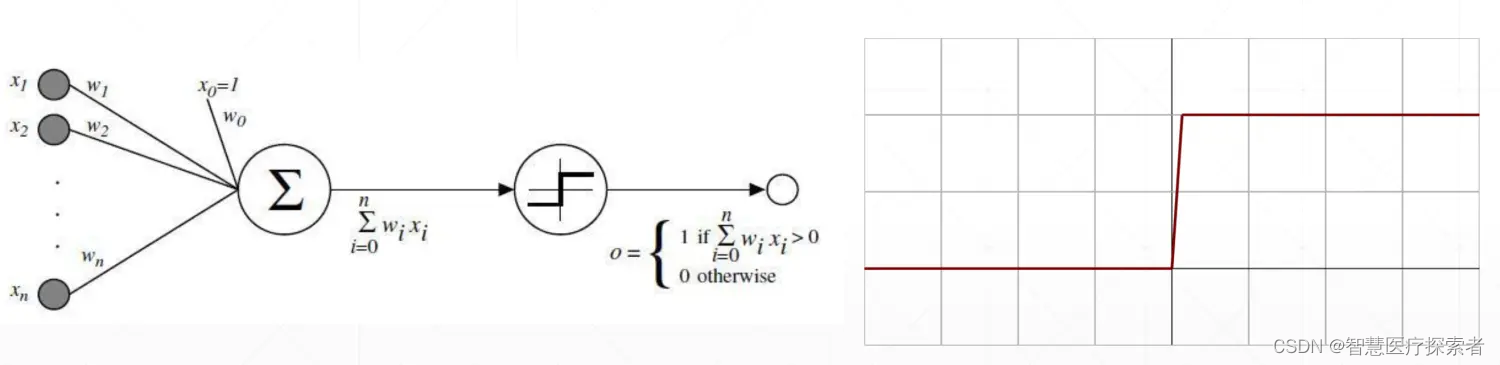
这里的激活函数就是阶跃函数,但在0处跃变且不可导。
进一步抽象出神经网络模型中神经元模型为:
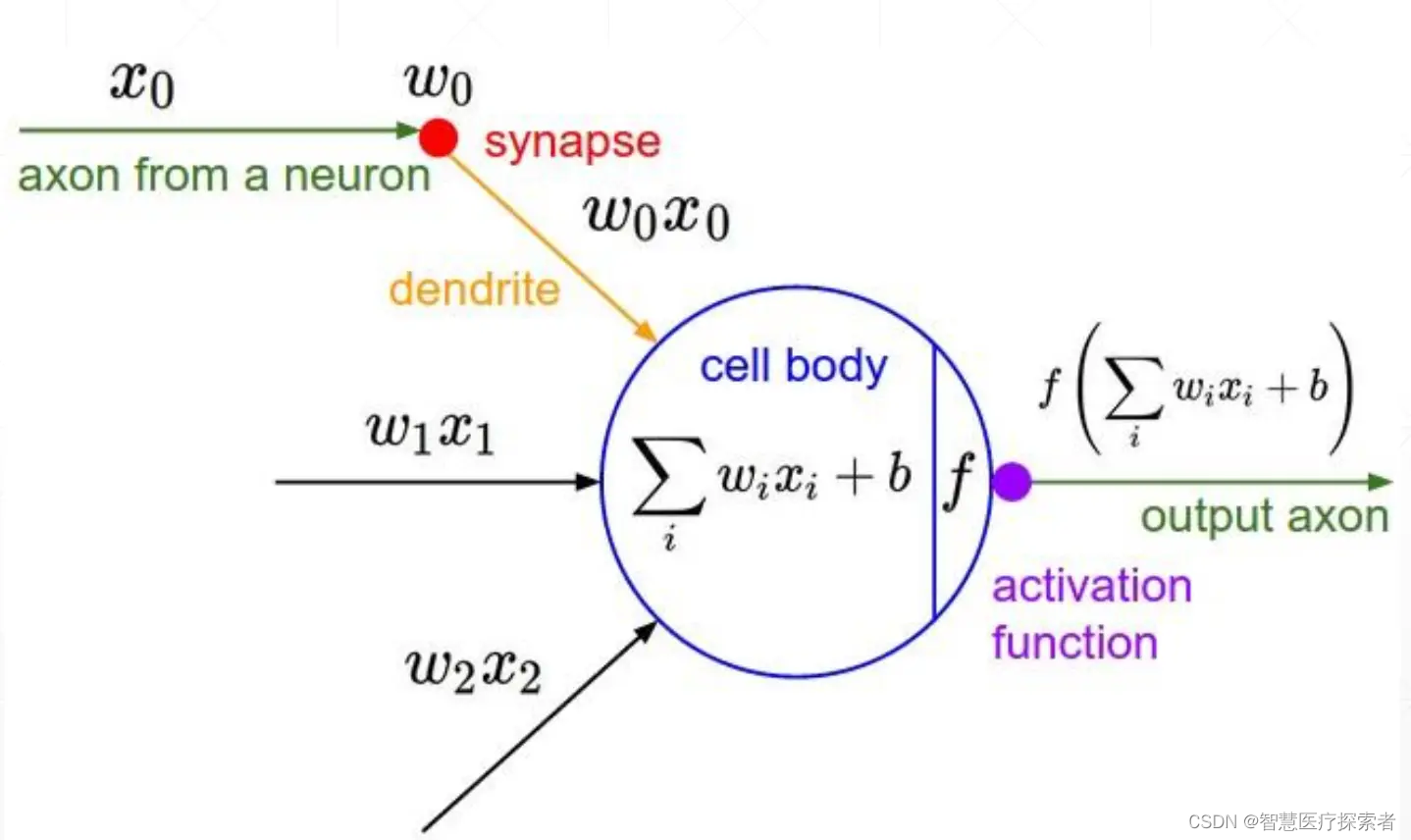
其中为激活函数
1.2 激活函数的作用
没有激活函数,可能简单的二分类问题都不能被优雅解决
现在有一个二分类问题,将三角形和圆点进行正确分类。这是一个线性不可分的问题(在这个平面里,找不到一条直线可以把图中的三角形和圆点完全分开),我们试着用神经网络解决这个问题。
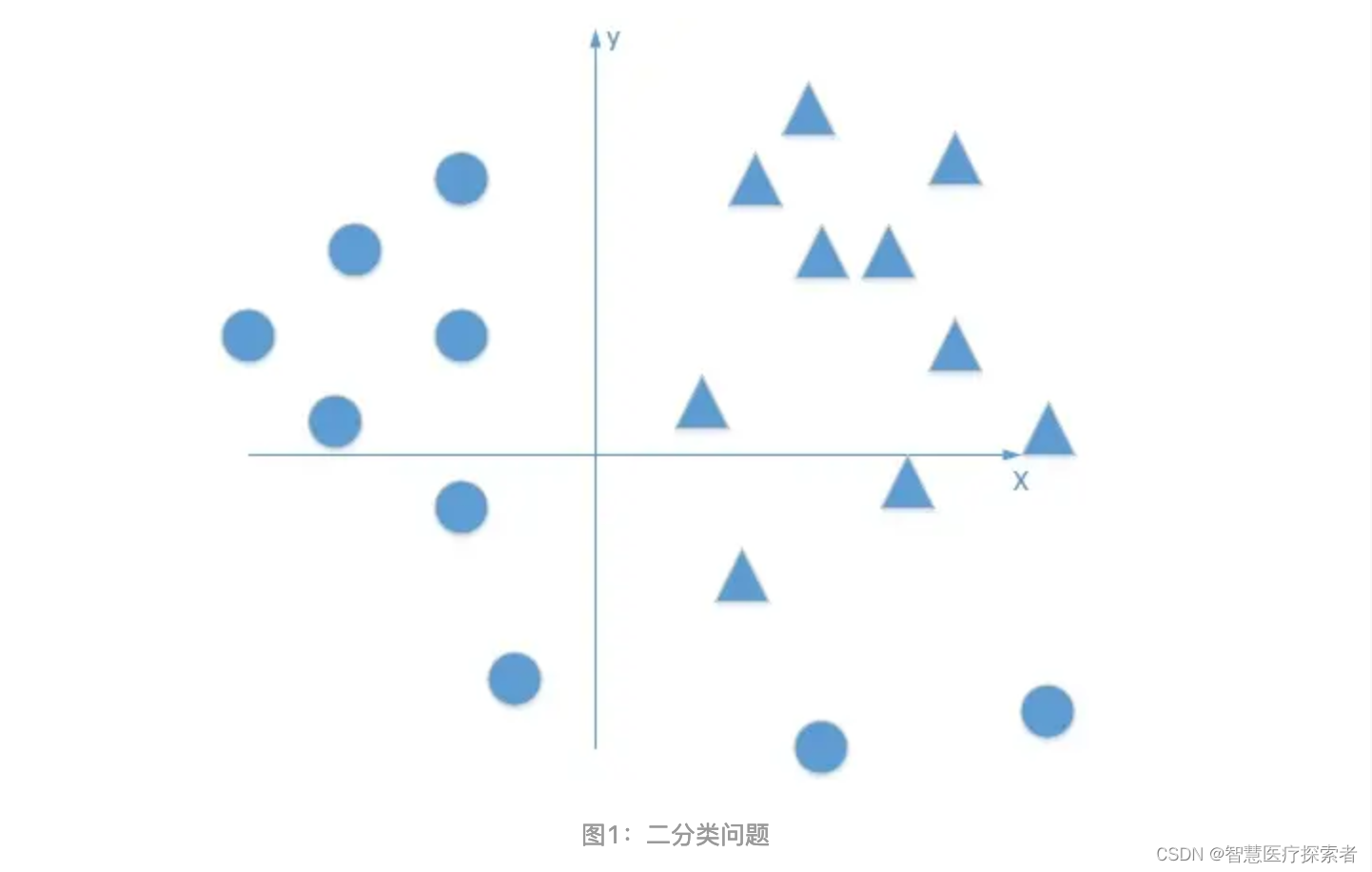
可能的解决思路:
- 用单层感知机(不带激活函数)
首先我们想到利用最简单的单层感知机来解决,单层感知机可以画出一条直线,把平面分开。
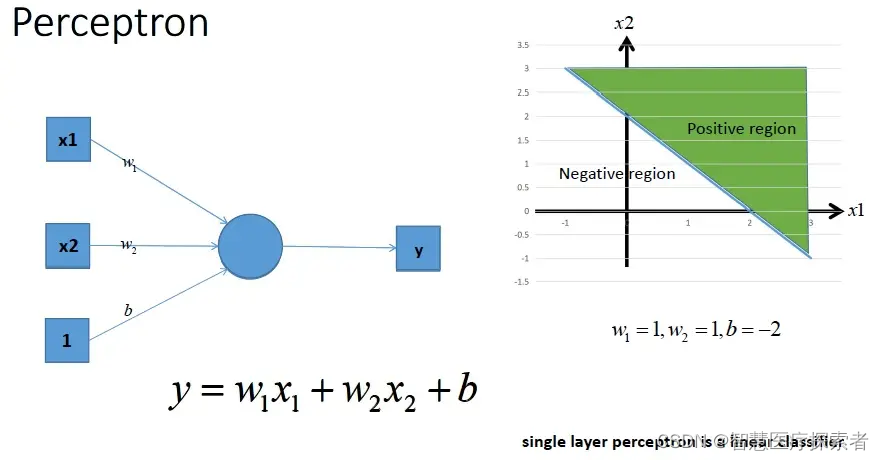
左图是没有激活函数的单层感知机结构,其中w1,w2是权重值,b是偏置值,它的工作原理是:输入一个样本(有两个特征x1,x2),如果y>0说明该样本是正类;如果y<0,说明该样本是负类。我们这里不讨论y=0的特殊情况。根据单层感知机的工作原理,我们画出右边的坐标图。
结论是:不带激活函数的单层感知机是一个线性分类器,不能解决线性不可分的问题。 不能解决二分类问题。
- 用多个感知机(不带激活函数)
不带激活函数的单层感知机解决不了问题,那我们就会想到用多个感知机进行组合,获得更强的分类能力,看看能不能解决我们的线性不可分问题。
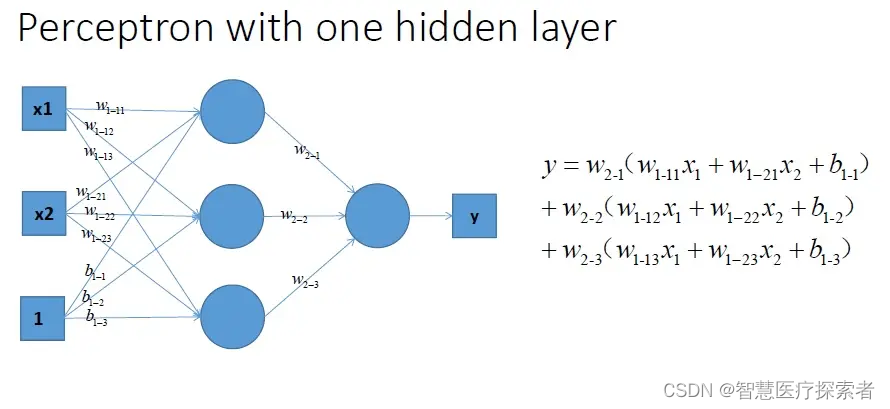
上图中,虽说模型变得复杂,表达能力更强一点,但y还是一个关于x1,x2的线性表达式。
结论是:合并后的多个感知器本质上还是一个线性分类器,还是解决不了非线性的问题。
进一步分析总结:不管是单层感知机还是多个感知器,只要不带激活函数,都只能解决线性可分的问题,解决不了我们的线性不可分问题。
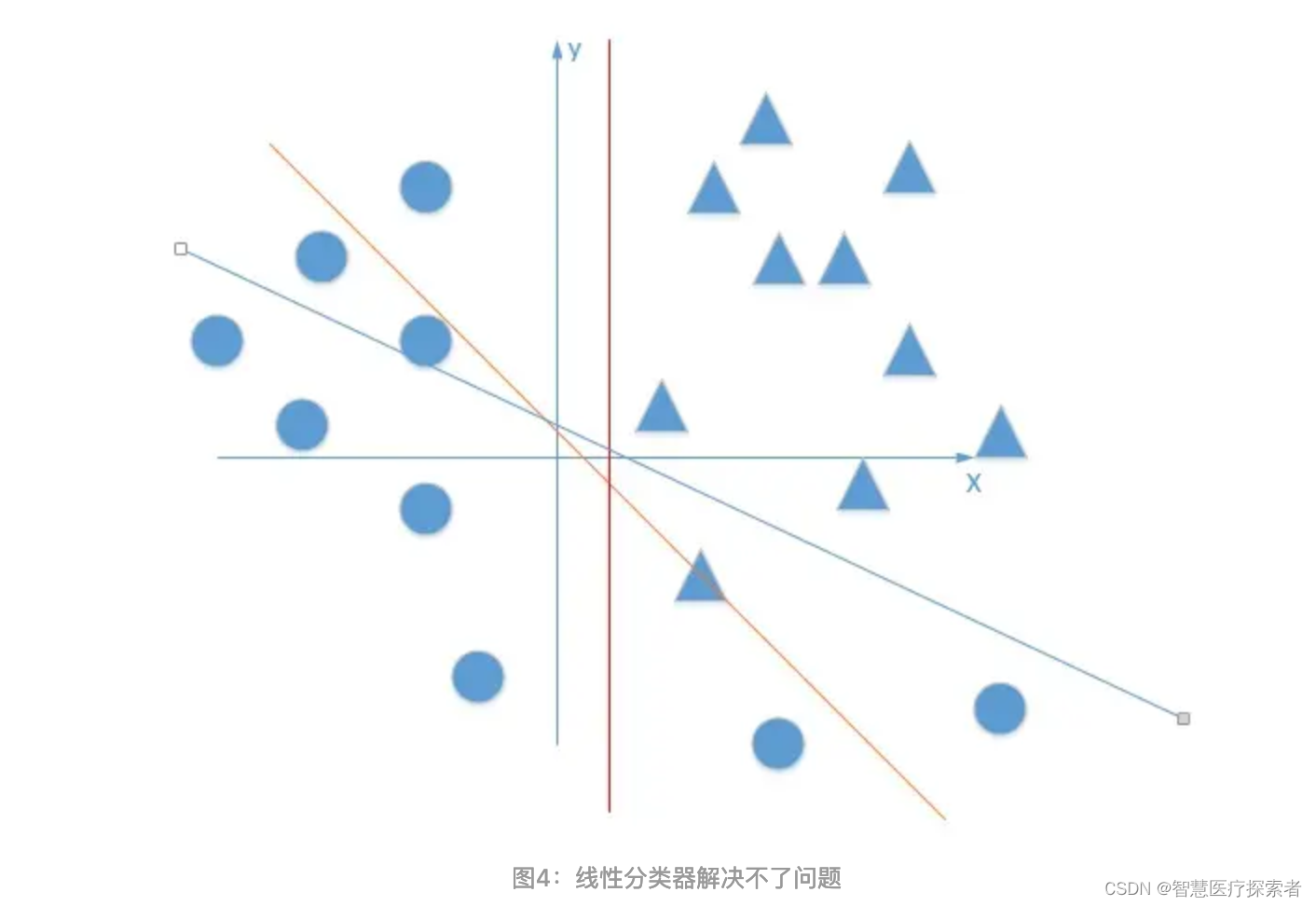
在上面的线性方程的组合过程中,我们其实类似的在做三条直线的线性组合,如图5所示。图5描述了,当我们直接用没有激活函数的分类器时,其实我们还是线性组合,最多也就是更复杂的线性组合罢了。
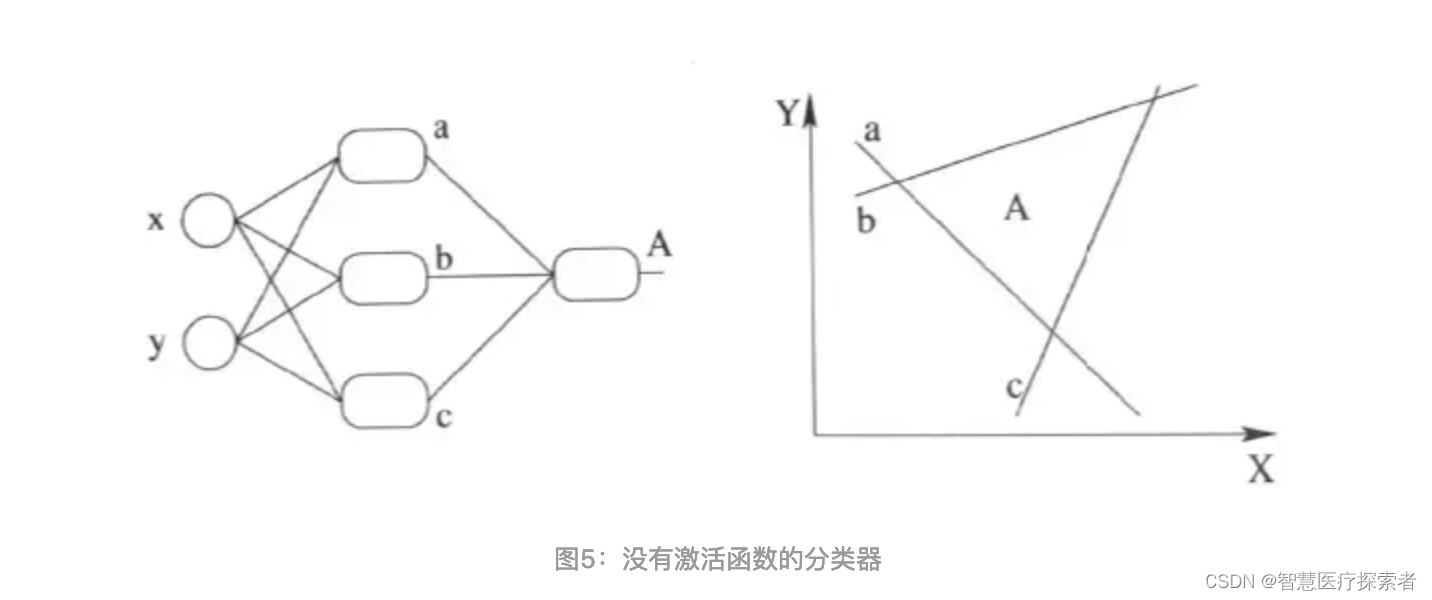
因此就需要来引入激活函数了。
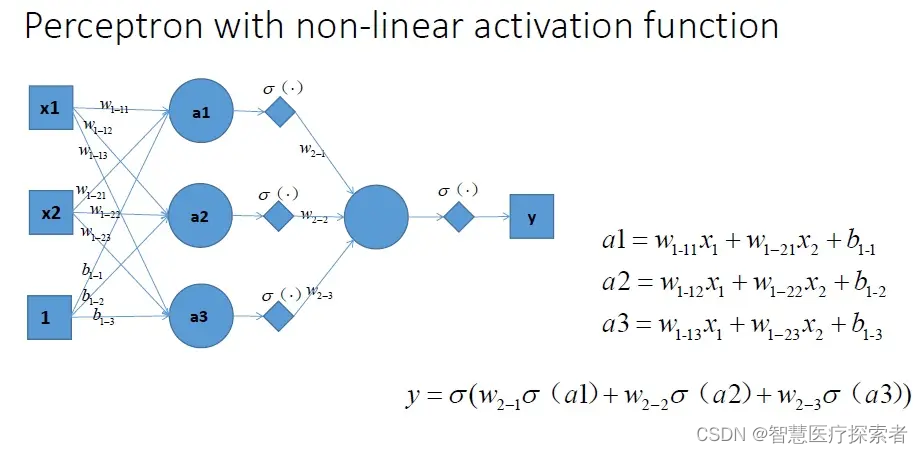
我们再设计一个神经网络,在所有的隐层和输出层加一个激活函数,这里激活函数我们就用Sigmoid函数,如下图所示,这样y出的就是一个非线性函数了,y的输出更复杂,有了这样的非线性激活函数以后,神经网络的表达能力更加强大了。能不能解决我们一开始提出的线性不可分问题呢?

我们把上图中的带有激活函数的单层感知机扩展到带有激活函数的多个神经元的情况。那么神经网络的表达能力更强,具体如下图所示。
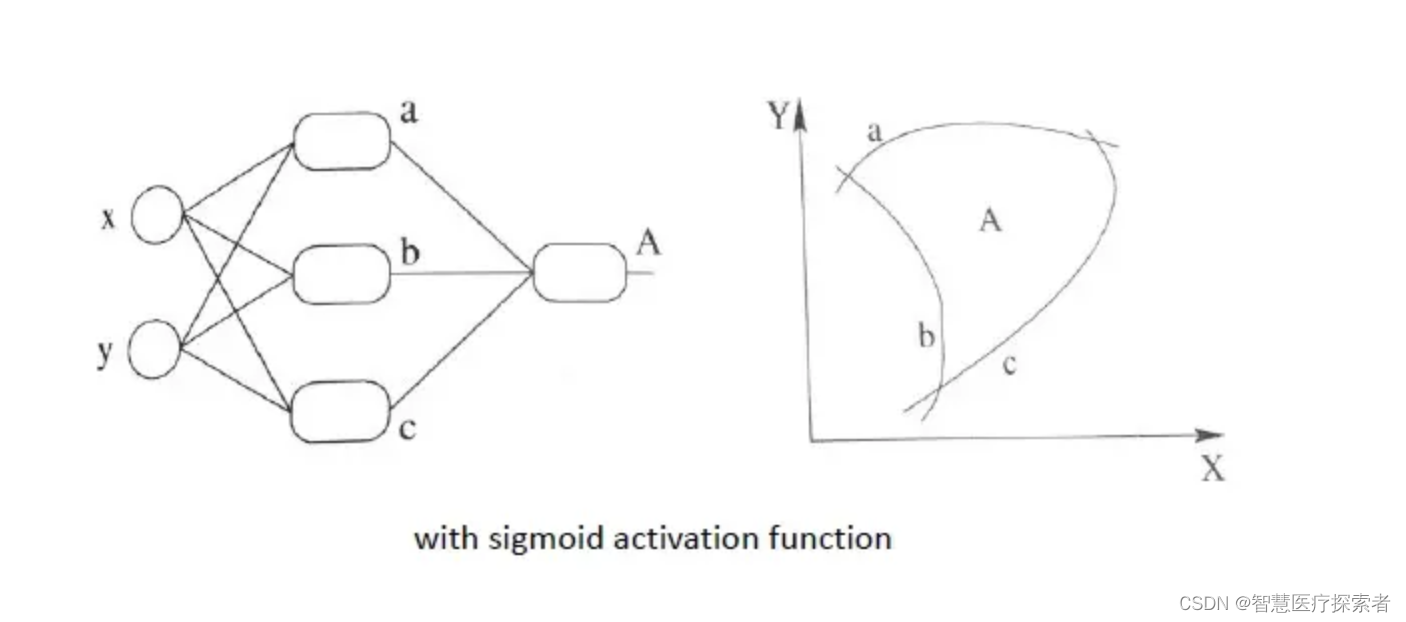
和之前相对应的非线性组合是图8所示的样子。这样看起来,似乎已经能解决我们线性不可分的问题了。最后,我们通过最优化损失函数的做法,通过不断的学习,能够学到正确分类三角形和圆点的曲线。
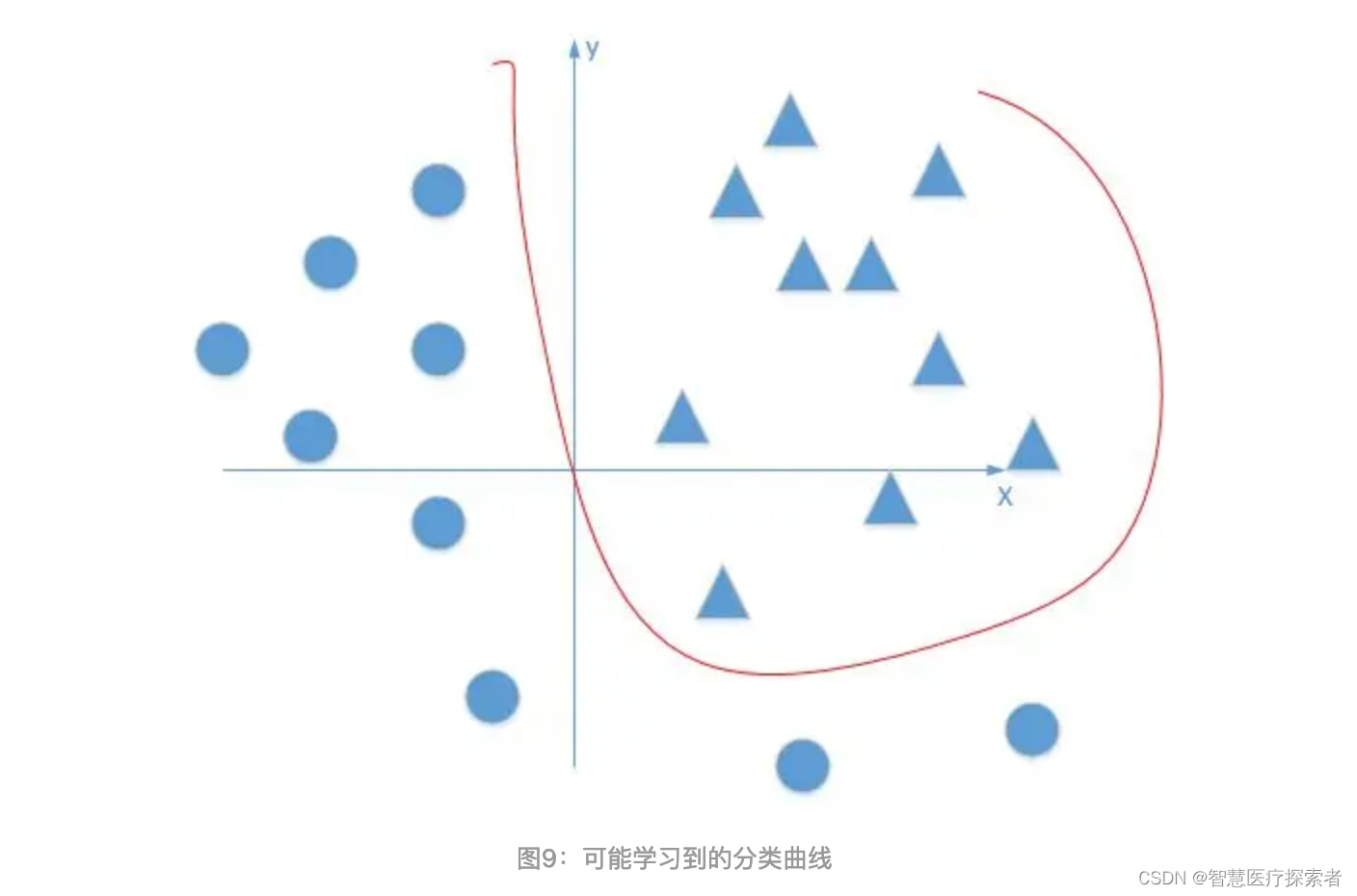
总结:激活函数是用来加入非线性因素的,提高神经网络对模型的表达能力,解决线性模型所不能解决的问题。要知道大部分问题是非线性问题,因此激活函数是必不可少的。
2 常用的激活函数
2.1 Sigmoid函数
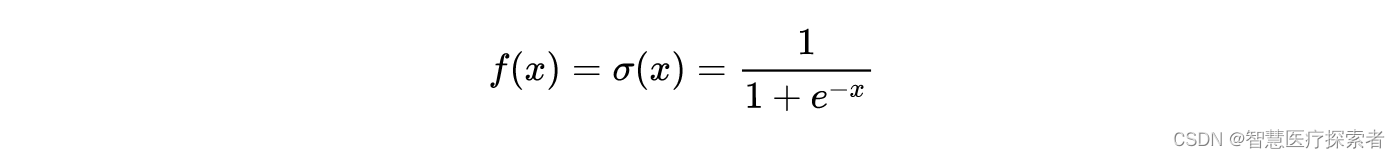
示例代码
import numpy as np
import matplotlib.pyplot as plt
sigmoid = lambda x: 1 / (1 + np.exp(-x))
x = np.linspace(-10, 10, 10)
y = np.linspace(-10, 10, 10)
fig = plt.figure()
plt.plot(y, sigmoid(y))
plt.grid(linestyle='--')
plt.xlabel('X Axis')
plt.ylabel('Y Axis')
plt.title('Sogmoid Function')
plt.xticks([-4, -3, -2, -1, 0, 1, 2, 3, 4])
plt.yticks([-2, -1, 0, 1, 2])
plt.xlim(-4,4)
plt.ylim(-2,2)
plt.show()运行代码显示
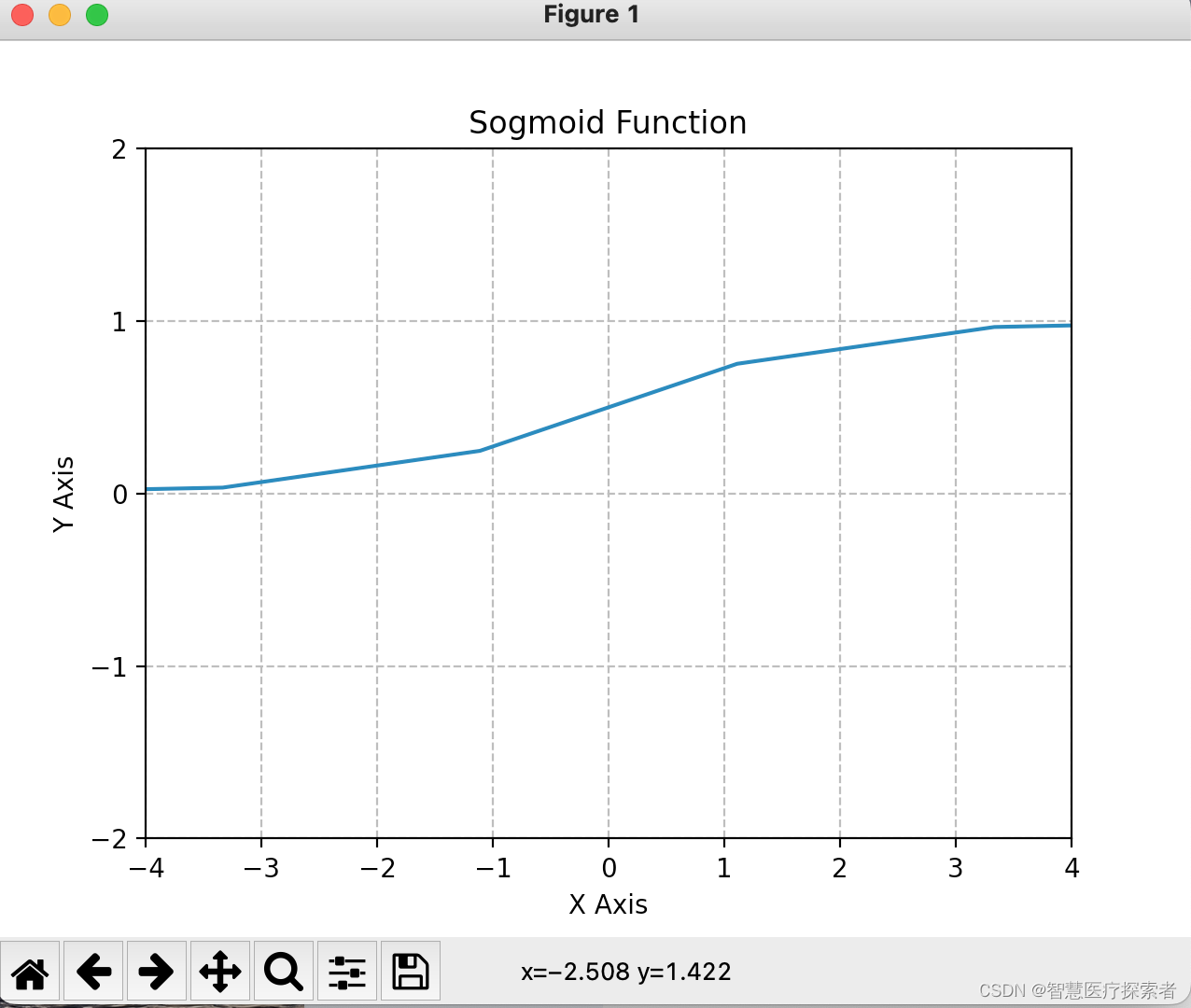
Sigmoid函数优点:
- 能够将函数压缩至区间[0, 1]之间,保证数据稳定,波动幅度小
Sigmoid函数缺点:
- 函数在两端的饱和区梯度趋近于0,当反向传播时容易出现梯度消失或梯度爆炸(不清楚为什么会梯度爆炸?)
- 输出不是0均值(zero-centered),这样会导致,如果输入为正,那么导数总为正,反向传播总往正方向更新,如果输入为负,那么导数总为负,反向传播总往负方向更新,收敛速度缓慢
- 运算量较大
2.2 tanh函数
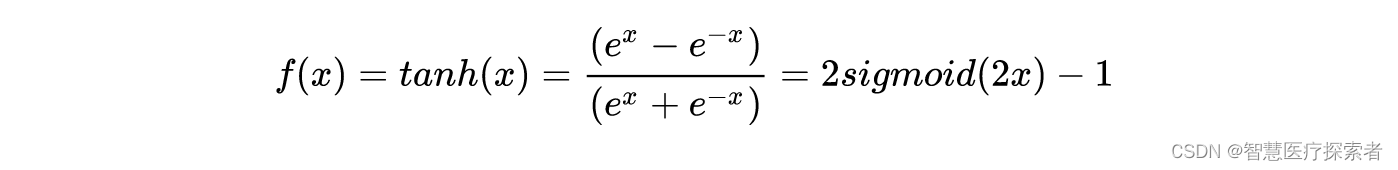
示例代码:
import numpy as np
import matplotlib.pyplot as plt
sigmoid = lambda x: 1 / (1 + np.exp(-x))
tanh = lambda x: 2*sigmoid(2*x)-1
x = np.linspace(-10, 10, 10)
y = np.linspace(-10, 10, 10)
plt.plot(y, tanh(y), 'b', label='linspace(-10, 10, 100)')
plt.grid(linestyle='--')
plt.xlabel('X Axis')
plt.ylabel('Y Axis')
plt.title('Tanh Function')
plt.xticks([-4, -3, -2, -1, 0, 1, 2, 3, 4])
plt.yticks([-4, -3, -2, -1, 0, 1, 2, 3, 4])
plt.xlim(-4,4)
plt.ylim(-4,4)
plt.show()代码运行结果:

tanh 函数优点:
- 解决了Sigmoid函数非0均值的问题,将函数压缩至区间[-1, 1]之间
pytorch中tanh函数的使用
tanh 函数缺点:
- 函数在两端的饱和区梯度趋近于0,当反向传播时容易出现梯度消失或梯度爆炸
- 运算量大
2.3 Relu函数

示例代码:
import numpy as np
import matplotlib.pyplot as plt
relu = lambda x: np.where(x>=0, x, 0)
x = np.linspace(-10, 10, 10)
y = np.linspace(-10, 10, 1000)
plt.plot(y, relu(y), 'b', label='linspace(-10, 10, 100)')
plt.grid(linestyle='--')
plt.xlabel('X Axis')
plt.ylabel('Y Axis')
plt.title('RuLU')
plt.xticks([-4, -3, -2, -1, 0, 1, 2, 3, 4])
plt.yticks([-4, -3, -2, -1, 0, 1, 2, 3, 4])
plt.xlim(-4,4)
plt.ylim(-4,4)
plt.show()代码运行结果:
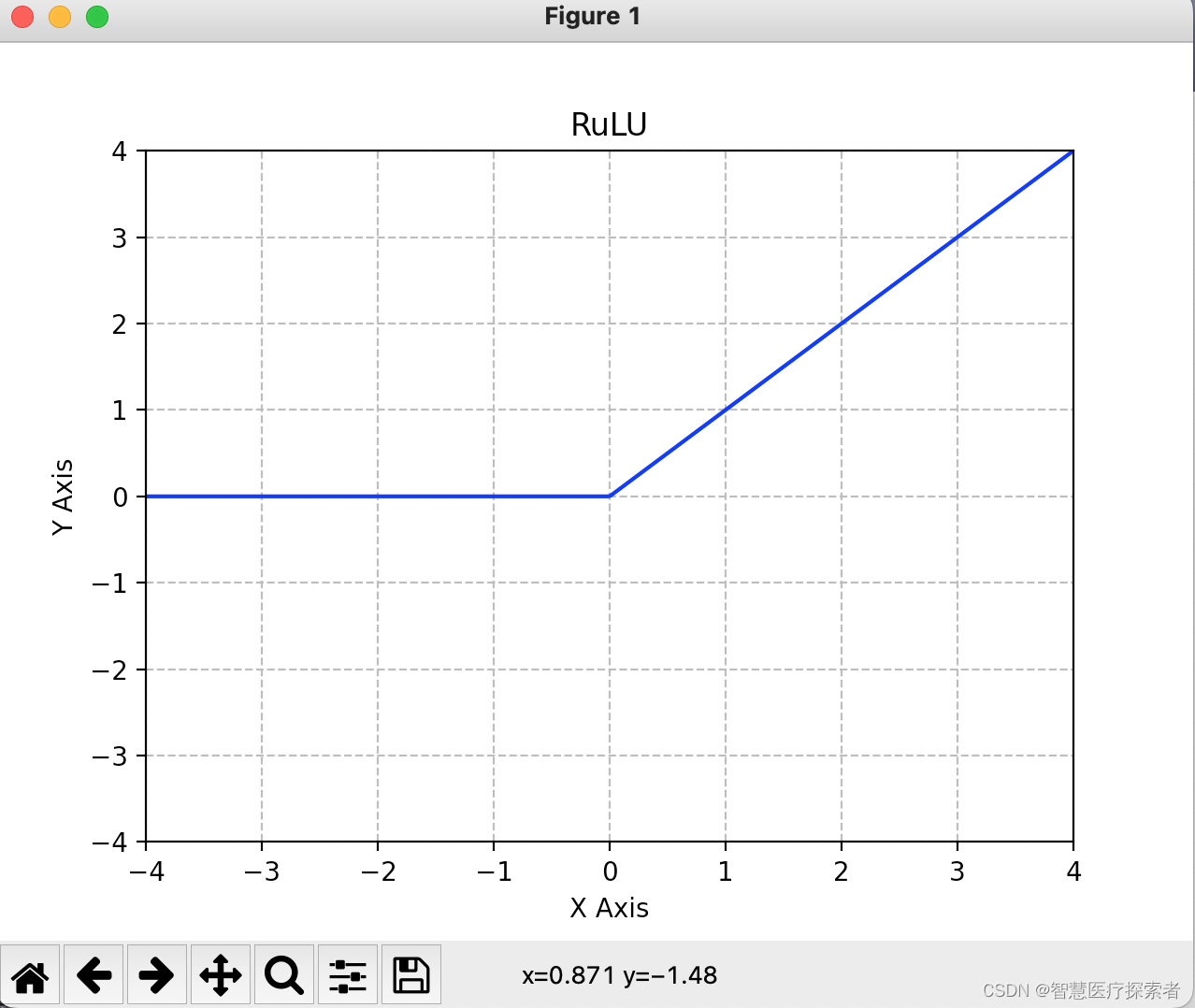
Relu优点:
- 梯度不饱和,收敛速度快
- 减轻反向传播时梯度弥散的问题
- 由于不需要进行指数运算,因此运算速度快、复杂度低
Relu缺点:
- 输出不是0均值(zero-centered)
- 对参数初始化和学习率非常敏感,设置不当容易造成神经元坏死现象,也就是有些神经元永远不会被激活(由于负部梯度永远为0造成)
2.4 leaky_relu函数

示例代码:
import numpy as np
import matplotlib.pyplot as plt
leakyrelu = lambda x: np.where(x>=0, x, 0.1*x)
x = np.linspace(-10, 10, 10)
y = np.linspace(-10, 10, 1000)
plt.plot(y, leakyrelu(y), 'b', label='linspace(-10, 10, 100)')
plt.grid(linestyle='--')
plt.xlabel('X Axis')
plt.ylabel('Y Axis')
plt.title('Leaky ReLU')
plt.xticks([-4, -3, -2, -1, 0, 1, 2, 3, 4])
plt.yticks([-4, -3, -2, -1, 0, 1, 2, 3, 4])
plt.xlim(-4, 4)
plt.ylim(-4, 4)
plt.show()代码运行结果:
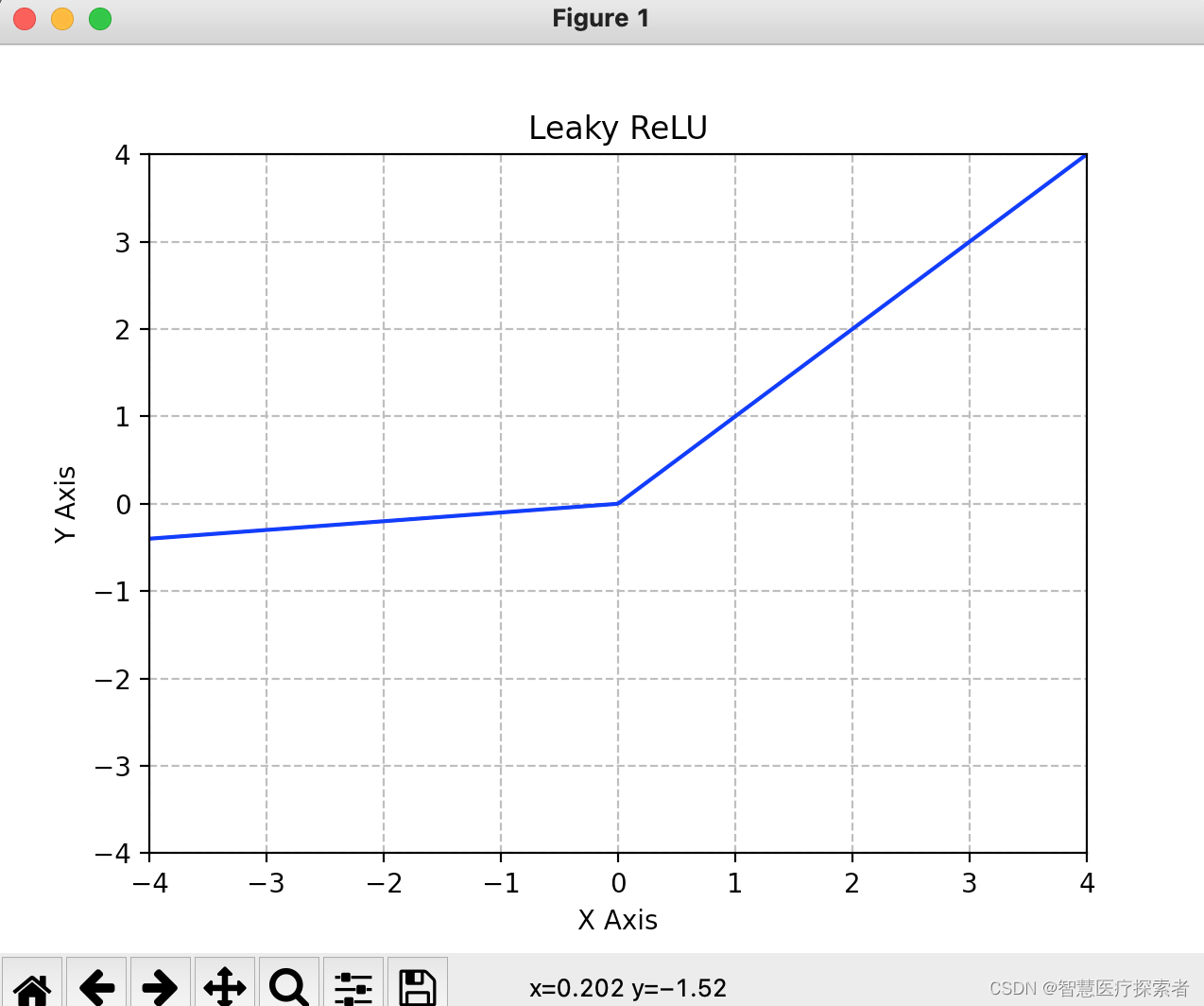
leaky_relu优点:
- Leaky Relu函数在输入为负值时,给予输入值一个很小的斜率,缓解了Dead Relu问题;
leaky_relu缺点:
- 理论上来说,该函数具有比Relu函数更好的效果,但是大量的实践证明,其效果不稳定,故实际中该函数的应用并不多。
2.5 其它激活函数
- RReLU:torch.nn.RReLU()
- PReLU:torch.nn.PReLU()
- Sofplus:torch.nn.Softplus()
- ELU:torch.nn.ELU()
- CELU:torch.nn.CELU()
- SELU:torch.nn.SELU()
- GELU:torch.nn.GELU()
- ReLU6:torch.nn.ReLU6()
- Softsign:torch.nn.Softsign()
- Hardtanh:torch.nn.Hardtanh()
- Threshold:torch.nn.Threshold()
- Tanhshrink:torch.nn.Tanhshrink()
- Softshrink:torch.nn.Softshrink()
- Hardshrink:torch.nn.Hardshrink()
- LogSigmoid:torch.nn.LogSigmoid()
- Softmin:torch.nn.Softmin()
- Softmax:torch.nn.Softmax()
- LogSoftmax:torch.nn.LogSoftmax()