引言：探索AR的神奇世界，我们将从二维码的诞生谈起。在这个科技的海洋中，二维码是如何帮助AR实现数据获取与位姿识别的呢？让我们一起揭开这层神秘的面纱！

一、二维码的由来

二维码是将数据存储在图形中的技术，在1994年由腾弘原（Masahiro Hara）发明。这里还有一个趣闻，腾弘原在发明二维码后放弃了申请专利，他说了这么一句话：“这种技术其实随便找个网络工具就能实现，所以这么简单的东西，我就不收专利费啦。”，这也是二维码得以广泛应用的原因之一。

于1999年，加藤博一等人率先将AR技术与二维码联系起来，结合二维码技术，开发了ARToolKit这一AR工具，这一工具在当今仍被广泛使用。让我们切回主题，谈一谈二维码是如何在AR中得到应用的。

二、二维码的工作原理

二维码可以为AR提供两样信息：ID和位姿，接下来让我们一一介绍

1.ID识别

首先，我们需要约定二维码的尺寸：
二维码存在 40 种尺寸，也就是二维码每行/列中的小方块的个数，在官方文档中，尺寸又被命名为 Version。尺寸与 Version 存在线性关系：Version 1 是 21×21 的矩阵，Version 2 是 25×25 的矩阵，每增加一个 Version，尺寸都会增加 4。 接下来，我们会为二维码划分区域，并编码：
 二维码的各部分都有自己的作用，基本上可被分为定位、功能数据、数据内容三部分：

1）定位区域：

定位图形：用于标记二维码矩形的大小；用三个定位图案即可标识并确定一个二维码矩形的位置和方向

定位图案分隔符：用白边框将定位图案与其他区域区分；

校正图形：只有在 Version 2 及其以上才会需要，用于矫正二维码的形变

2）功能数据：

格式信息：存在于所有尺寸中，存放格式化的数据

版本信息：用于 Version 7 以上，需要预留两块 3×6 的区域存放部分版本信息；

3）数据内容：剩余部分存储二值化的数据内容，例如黑色方块代表1，白色方块代表0，此外数据内容还包括补齐符、纠错码、结束符等

接下来是识别：

输入图像，通过相机捕获图像

图像二值化，通过图形算法将图像进行二值化处理，即将图像变为黑白两色的图像

提取具有一定面积的连续区域

提取矩形区域的轮廓

对矩形区域内部的图案进行解析，识别标识内容
由此，相机可以“认出”二维码及二维码的内容，将二维码的功能数据中的ID提取出来，这些ID可以是网站，可以是一个登录申请，也可以是激活设备某个功能的字符串

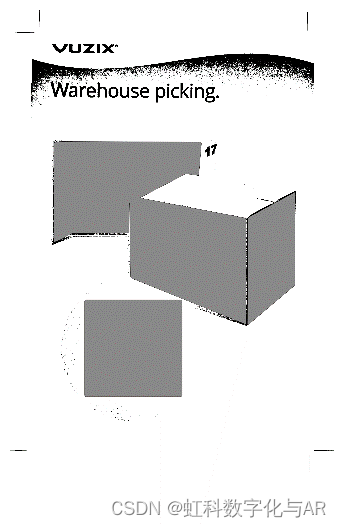
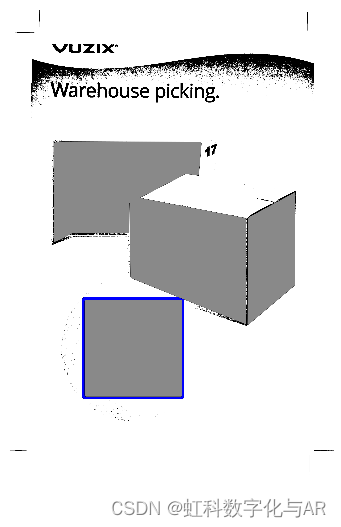
2.位姿识别

此外，二维码也可帮助AR设备进行位姿识别，什么是位姿识别呢？就是让设备知道自己和二维码之间的距离和相对的姿态关系，也即二维码离我多远？二维码是左右倾斜、还是前后俯仰？
位姿识别过程与ID识别类似，不过不同之处是，在提取各区域的轮廓后，位姿识别最需要的信息，是二维码区域4个角的顶点坐标（Xi​,Yi​）。

首先，我们用示意图表示摄像机的坐标系、图像坐标系（摄像机拍摄的平面图形的坐标系）、标识坐标系（二维码在现实中所在的坐标系）

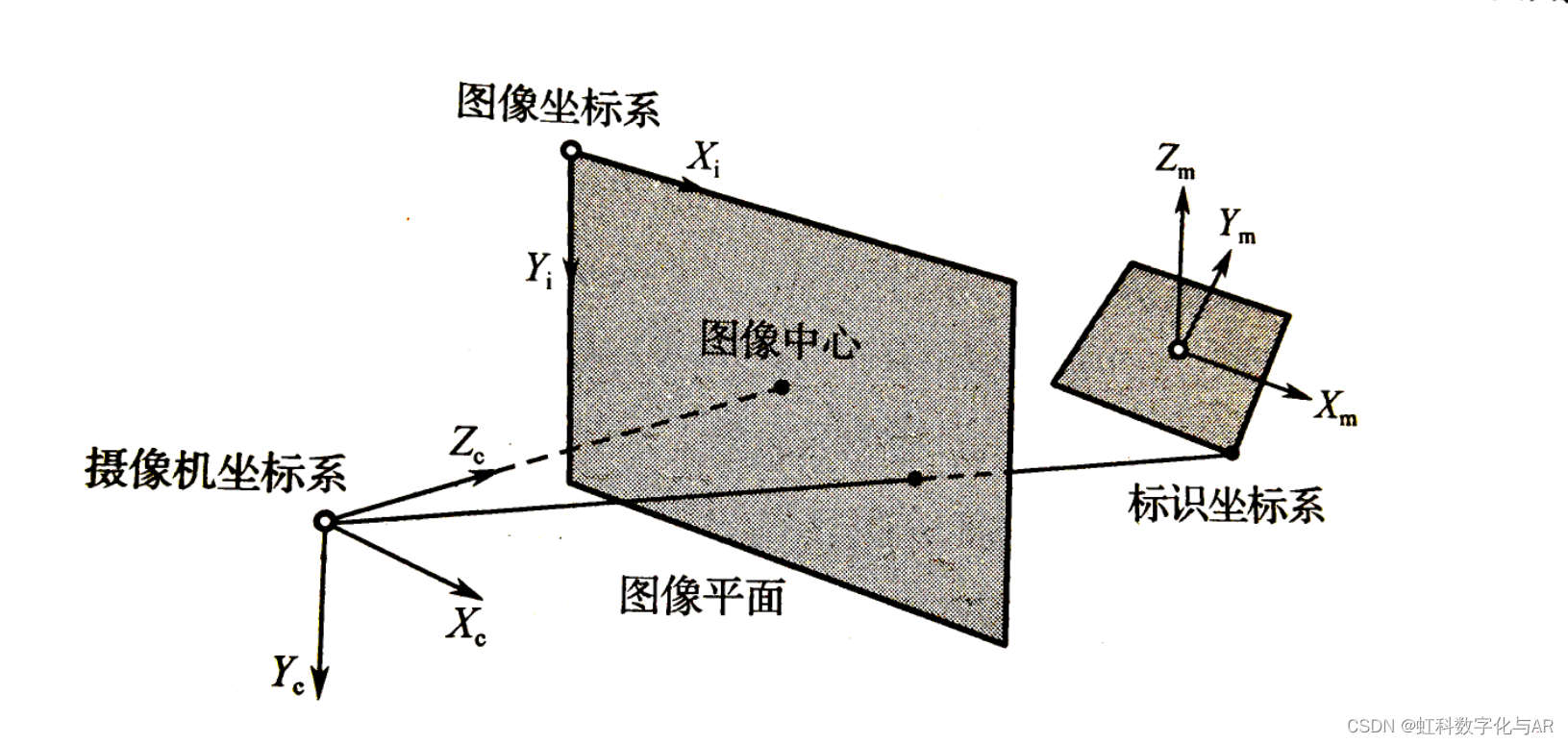我们通过相机拍摄到的图像坐标系的点（Xi​,Yi​），与相机内置的矫正矩阵K，可以求得旋转变换矩阵R与平移向量t，其中，R表示二维码相对相机发生的旋转，t表示二维码相对相机发生的平移
大致求解流程如下：

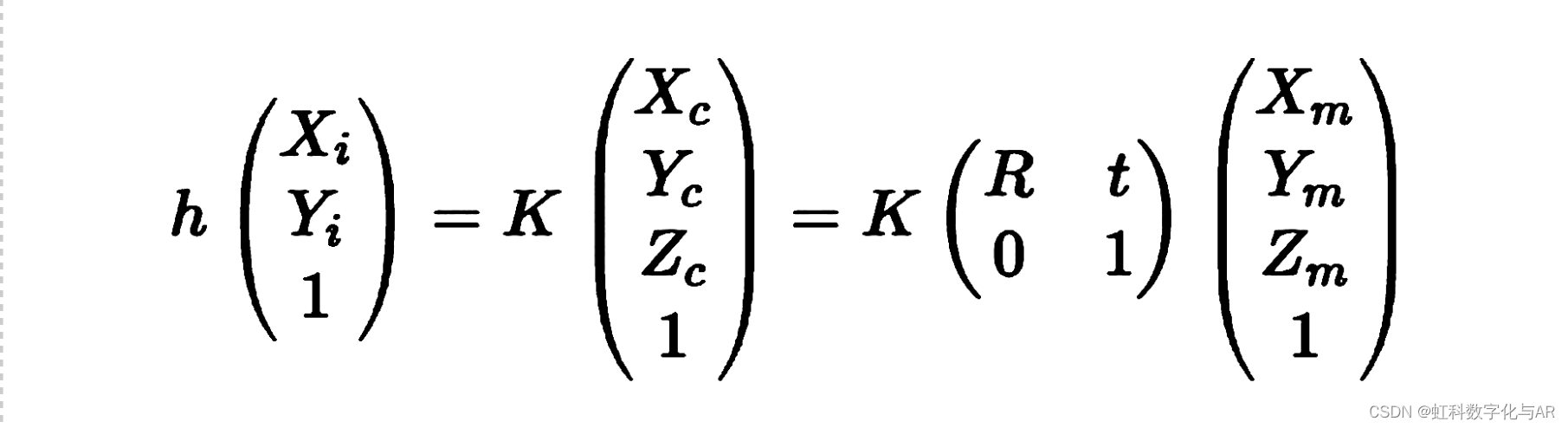结合对二维码在图像坐标系的4个顶点所得的4项公式，我们便可求得矩阵R与t，得到二维码的旋转方位与平移方位，也可由此利用二维码实现各式的AR应用。

三、各式各样的二维码

以上是对二维码工作原理的简单介绍，而在实际生活中，二维码的形态也在不断更迭，除了我们日常见到的二维码，现在已经出现了防遮挡二维码、红外隐形二维码、随机点二维码、微透镜片二维码等，这些新型二维码，也可以和AR结合，帮助我们更好地与现实世界的物体进行交互。

参考文献

[1]:版权声明：本文为CSDN博主「琦小虾」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。 原文链接：二维码生成原理及解析代码 

[2]:《增强现实（AR）技术权威指南》