【模板】KMP算法笔记

news2024/11/29 12:33:44

练习链接：【模板】KMP - 洛谷

题目：

输入
`ABABABC ABA`

输出
1 3 0 0 1

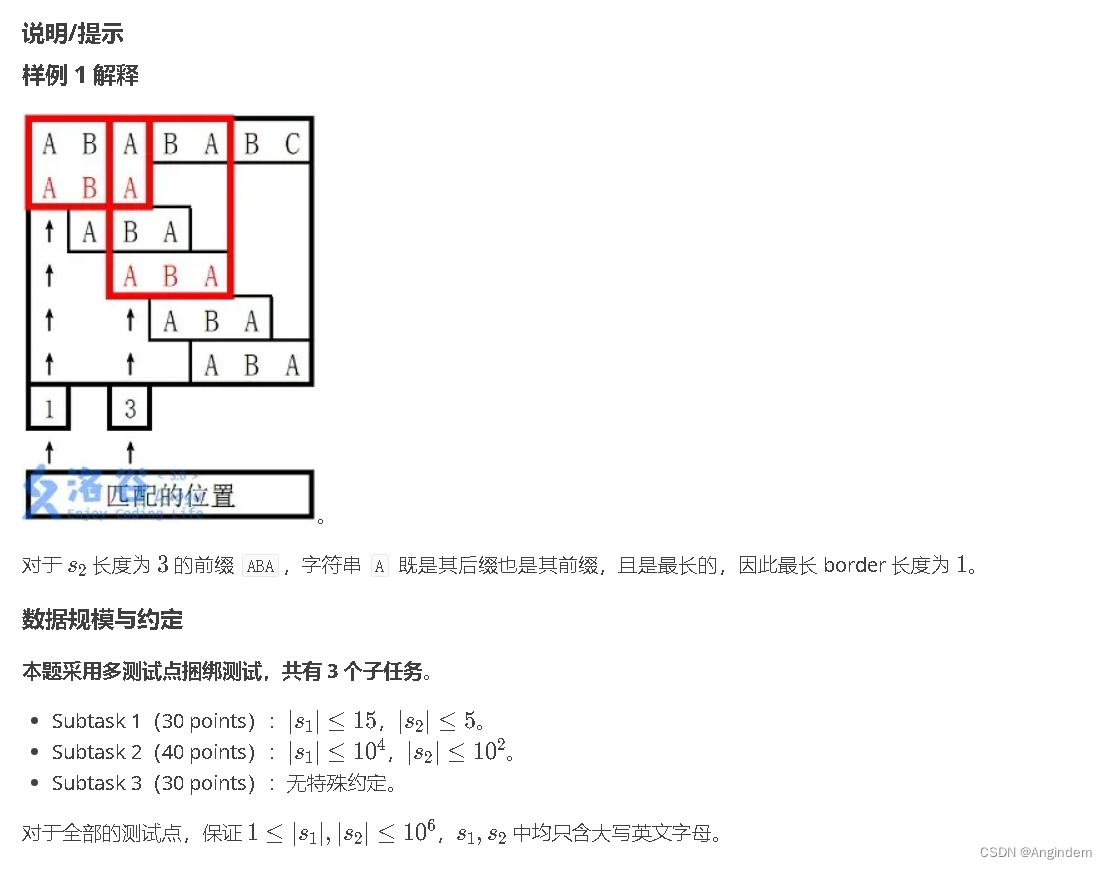
思路：

根据题意，用到的是KMP算法，KMP算法思想是通过一个一个匹配首字母的原理进行整个匹配效果，当某个首字母不匹配的时候，就跳跃相差对应的字符串长度，达到优化检索的效果。

所以 ne 数组是用来存储相应字符所对应的下标的。

注意：我们应该先预处理用于匹配的字符串 ne 数组，可以理解为先预处理短的字符串的 ne数组

代码详解如下：

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#define endl '\n'
#define YES puts("YES")
#define NO puts("NO")
#define umap unordered_map
#define All(x) x.begin(),x.end()
//#pragma GCC optimize(3,"Ofast","inline")
#define IOS std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10;
string p,t;

int ne[N],n,m;
inline void KMP()
{
	// 预处理模式串，即短的字符串
	for(int i = 2,j = 0;i <= n;++i)
	{
		// 匹配相对应的字符下标j
		while(j && p[i] != p[j + 1]) j = ne[j];
		if(p[i] == p[j + 1]) ++j;
		
		ne[i] = j;	// 更新ne数组
	}
	
	// 开始 KMP 匹配  t 字符串相应位置 与 p 字符串匹配是否一致
	for(int i = 1,j = 0;i <= m;++i)
	{
		while(j && t[i] != p[j + 1]) j = ne[j];
		if(t[i] == p[j + 1]) ++j;
		
		// 当我们的 j 下标与 模式串p 长度相同的时候，说明匹配成功
		if(j == n)
		{
			// 输出相应位置，为当前下标 - 字符串长度为  所匹配成功的相应下标
			cout << i - j + 1 << endl;
			
			j = ne[j]; 	// 更新 j 下标，获取下一个相应字符的 ne数组
		}
	}
	
}

inline void solve()
{
	cin >> t >> p;
	
	n = p.size();
	m = t.size();
	p = " " + p;
	t = " " + t;
	
	KMP();	// KMP 算法
	
	// 输出 ne 数组
	for(int i = 1;i <= n;++i)
	{
		cout << ne[i] << ' ';
	}
}

int main()
{
//	freopen("a.txt", "r", stdin);
//	IOS;
	int _t = 1;
//	cin >> _t;
	while (_t--)
	{
		solve();
	}
	return 0;
}