给你二叉树的根节点 root 和一个整数 limit ，请你同时删除树中所有 不足节点 ，并返回最终二叉树的根节点。假如通过节点 node 的每种可能的 “根-叶” 路径上值的总和全都小于给定的 limit，则该节点被称之为 不足节点 ，需要被删除。叶子节点，就是没有子节点的节点。

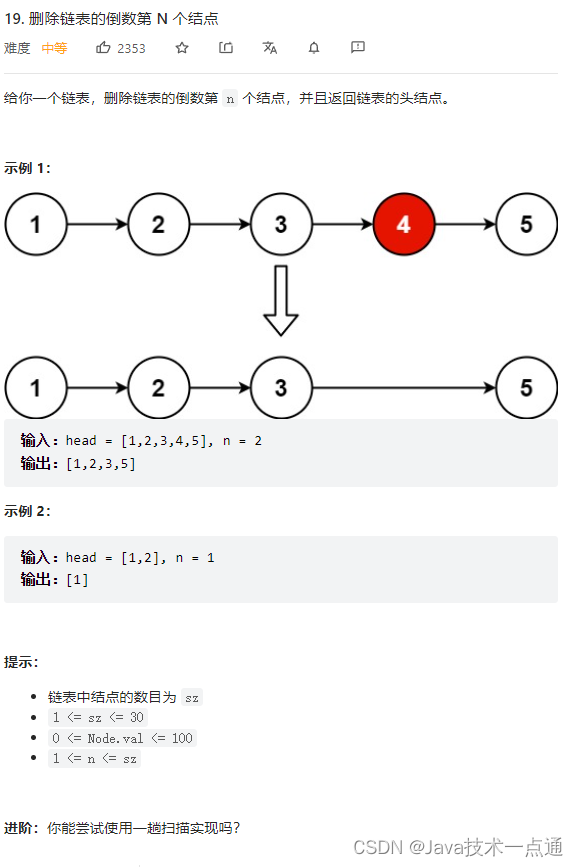
示例 1：

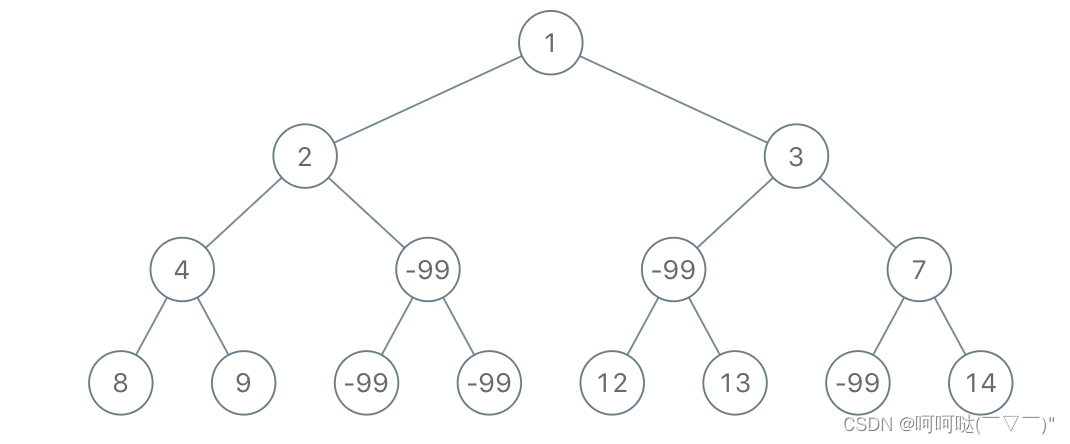
输入：root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1
输出：[1,2,3,4,null,null,7,8,9,null,14]

示例 2：

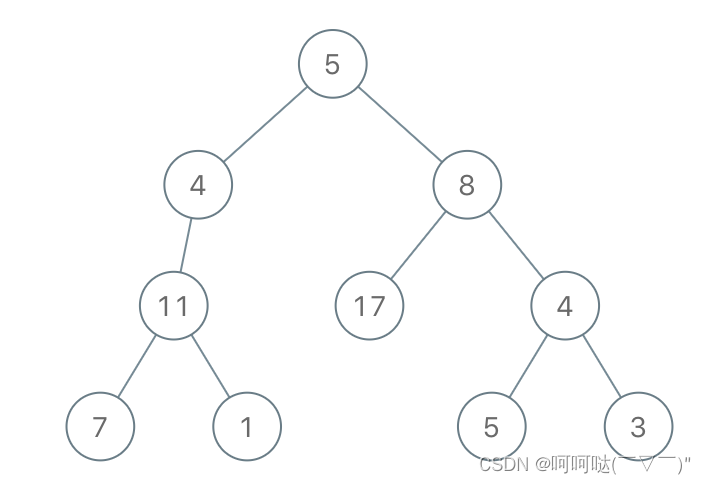
输入：root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22
输出：[5,4,8,11,null,17,4,7,null,null,null,5]

示例 3：

输入：root = [1,2,-3,-5,null,4,null], limit = -1
输出：[1,null,-3,4]

class Solution {
public:
    bool dfs(TreeNode* node,int limit,int sumPath) {
        sumPath += node->val;
        if(node->left == node->right) {
            return sumPath>=limit;
        } 
        if(node->left && dfs(node->left,limit,sumPath)==false)  { // 左
            node->left = nullptr;
        }
        if(node->right && dfs(node->right,limit,sumPath)==false)  { // 右
            node->right = nullptr;
        }
        return node->left || node->right;
    }
    TreeNode* sufficientSubset(TreeNode* root, int limit) {
        return dfs(root,limit,0) ?root:nullptr;
    }
};

class Solution {
public:
    bool dfs(TreeNode* node,int limit) {
        limit-=node->val;
        if(node->left == node->right) {
            return limit>0?false:true;
        } 
        if(node->left && dfs(node->left,limit)==false)  { // 左
            node->left = nullptr;
        }
        if(node->right && dfs(node->right,limit)==false)  { // 右
            node->right = nullptr;
        }
        return node->left || node->right;
    }
    TreeNode* sufficientSubset(TreeNode* root, int limit) {
        return dfs(root,limit) ?root:nullptr;
    }
};

class Solution {
public:
    TreeNode* sufficientSubset(TreeNode* root, int limit) {
        limit-=root->val;
        if(root->left == root->right) { // root 是叶子
            return limit > 0 ? nullptr : root;
        } 
        if(root->left)  { // 左
            root->left = sufficientSubset(root->left,limit);
        }
        if(root->right)  { // 右
            root->right = sufficientSubset(root->right,limit);
        }
        // 如果有儿子没被删除，就不删 root，否则删 root
        return root->left || root->right ?root:nullptr;
    }
};

还有详细图解待续~，尽情期待！