0.基础知识

0.1图的存储结构

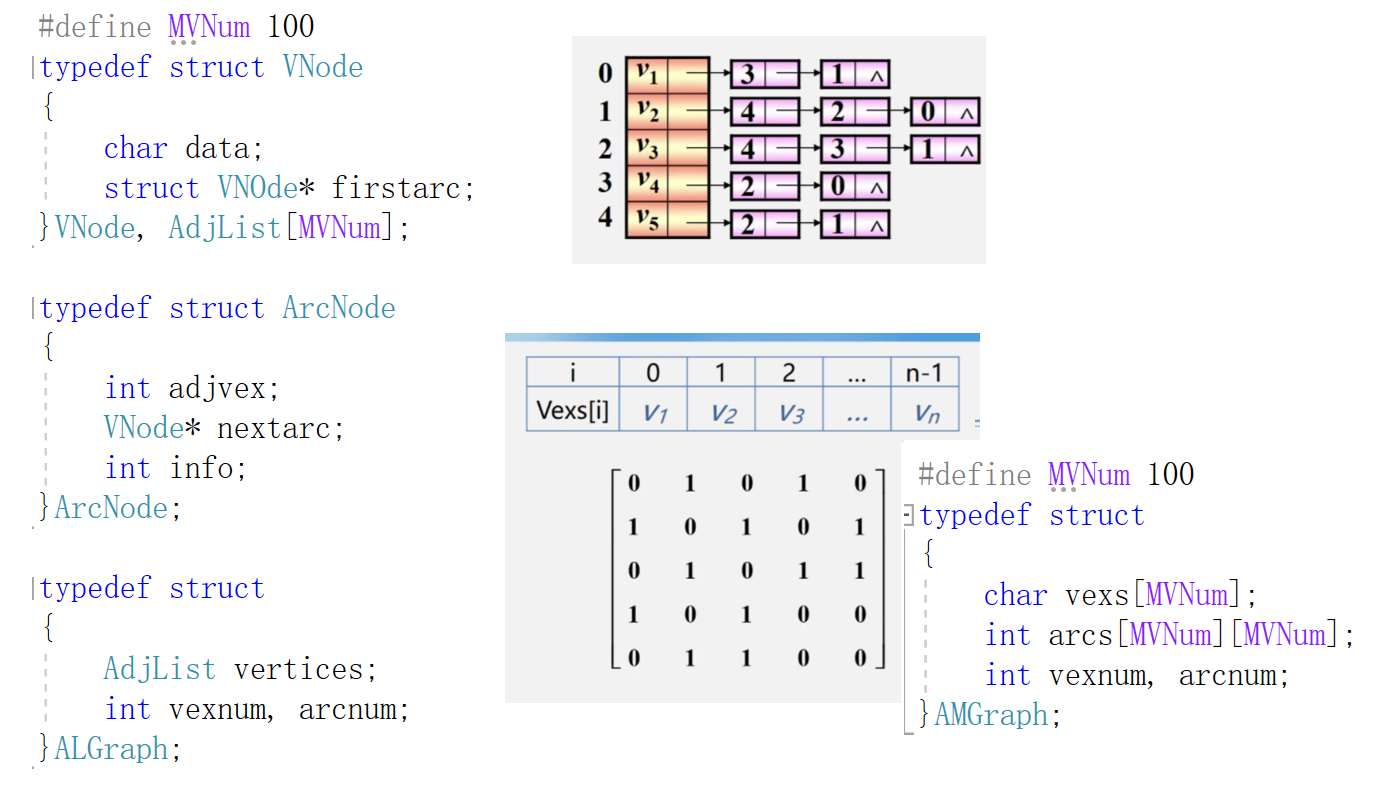
0.2算法复杂度

1.BFS和DFS

邻接矩阵表示: 时间复杂度 = O(N^2)
邻接矩阵表示: 时间复杂度 = O(N+E)
空间复杂度均为O(N)

稠密图适于在邻接矩阵上进行深度遍历
稀疏图适于在邻接表_上进行深度遍历

2.Prim和Kruskal

Prim: O(N^2) 稠密图
Kruskal: O(eloge)[边数] 稀疏图
Minimum Spanning Tree: MST

1.最小生成树

1.1Prim算法

1.算法思想

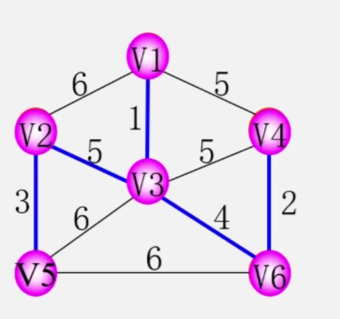
1. 所有的顶点被分为两类 被加入到MST的A类 未被加入到MST的B类
2. 从B类中任选一个顶点V 放入A类 从能跟A类连接且不在MST的这些边中选出一条权值最小的边作为MST的构成部分
3. V所连的那个顶点入MST 依次2 3直到所有顶点入MST

2.Prim代码实现

1. 搞一个结构体数组 下标i表示每个顶点的编号 左域存顶点Vx 表示Vi到Vx 右域存距离 表示Vi到Vx的距离
2. 从起始点u作为A类的第一个顶点开始 从矩阵中取出B类所有顶点到A类新增顶点(此时是u) 的距离放入对应右域 左域放B类新增顶点 此时结构体数组表示B类所有顶点到A类新增顶点的距离
3. 在当前结构体数组中取出右域值最小的下标index 表示编号为index的顶点到A类顶点距离最短 Vindex将作为下一个加入A类的顶点 此时第一条路径已求出 输出
4. Vindex顶点在结构体数组的右域值设0 表示已入A类[0: 已入A类正无穷: 不存在边 其他值: 距离长度]
5. 遍历矩阵编号为index的那一行 取出每个顶点到Vindex的距离 与 每个顶点到旧A类顶点距离比较 如果因为Vindex的新加入使得B类顶点到A类顶点出现较小值 则替换 比如:Vj到Vindex距离比Vj到旧顶点距离小 Vj在结构体数组中的左域放Vindex 对应距离也替换
6. 继续345

#include <iostream>
#define MVNum 10
#define MaxInt 32767 
using namespace std;

struct edge
{
    char adjvex;
    int lowcost;
}closedge[MVNum];

typedef struct 
{
    char vexs[MVNum];
    int arcs[MVNum][MVNum];
    int vexnum, arcnum;
}AMGraph;


int LocateVex(AMGraph G, char v)
{
    for (int i = 0; i < G.vexnum; i++)
    {
        if (G.vexs[i] == v)
            return i;
    }
    return -1;
}

int CreateUDN(AMGraph& G) 
{
    cin >> G.vexnum >> G.arcnum;
    for (int i = 0; i < G.vexnum; i++)
        cin >> G.vexs[i];
    for (int i = 0; i < G.vexnum; i++)
    {
        for (int j = 0; j < G.vexnum; j++)
            G.arcs[i][j] = MaxInt;
    }
    for (int k = 0; k < G.arcnum; k++) 
    {
        char v1, v2;
        int w;
        cin >> v1 >> v2 >> w;
        int i = LocateVex(G, v1);
        int j = LocateVex(G, v2);
        if (i != -1 && j != -1) 
            G.arcs[i][j] = G.arcs[j][i] = w;
    }
    return 0;
}


int Min(AMGraph G)
{
    int min = MaxInt;
    int min_index;
     for (int i = 0; i < G.vexnum; i++)
    {
        if (closedge[i].lowcost != 0 && closedge[i].lowcost < min)
        {
            min = closedge[i].lowcost;
            min_index = i;
        }
    }
    return min_index;
}

void Prim(AMGraph G, char u) 
{
    int index = LocateVex(G, u);
   
    for (int i = 0; i < G.vexnum; i++) 
    {
        if (i != index)
        {
            closedge[i].adjvex = u;
            closedge[i].lowcost = G.arcs[index][i];
        }
    }
    //u到u距离为0
    closedge[index].lowcost = 0;

    for (int i = 1; i < G.vexnum; i++)
    {
        index = Min(G);
        cout << closedge[index].adjvex << "->" << G.vexs[index] << endl;
        closedge[index].lowcost = 0;

        for (int j = 0; j < G.vexnum; j++) 
        {
            if (G.arcs[index][j] < closedge[j].lowcost)
            {
                closedge[j].adjvex = G.vexs[index];
                closedge[j].lowcost = G.arcs[index][j];
            }
        }
    }
}

int main()
{
    AMGraph G;
    CreateUDN(G);
    char u;
    cin >> u;
    Prim(G, u);
    return 0;
}

1.2Kruskal算法

1.算法思想

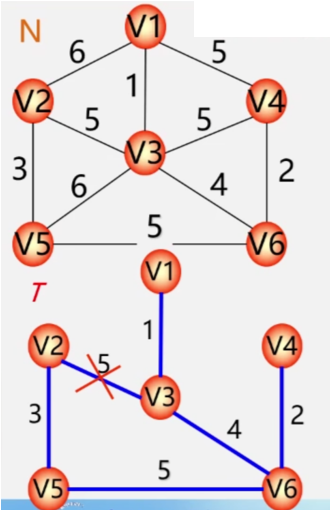
假设只有顶点没有边 从所有的边中取一条权值最小且不会形成环的边 直至构成一棵最小生成树

2.Kruskal代码实现[demo]

2.最短路径

2.1问题抽象:

在有向网中A点(源点)到达B点(终点)的多条路径中，寻找一条各边权值之和最小的路径，即最短路径。

最短路径与最小生成树不同，路径上不一定包含n个顶点,也不一定包含n- 1条边。

2.2两种常见的最短路径问题:

单源最短路径: Dijkstra (迪杰斯特拉) 算法
所有顶点间的最短路径: Floyd (弗洛伊德)算法

1.Dijkstra: 单源最短路径O(N^2)

可以求出V0到V1~V6的分别的最短路径

按路径长度递增次序产生最短路径

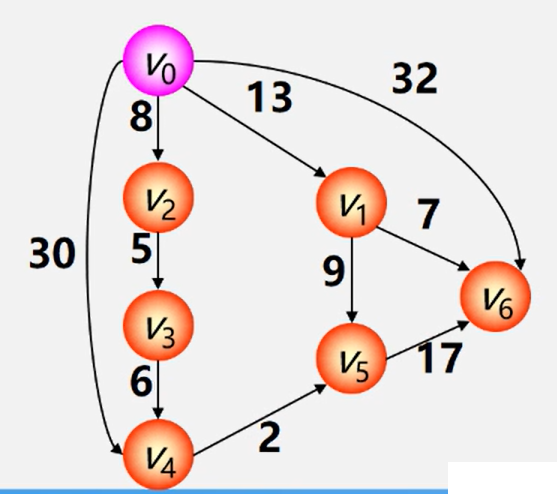
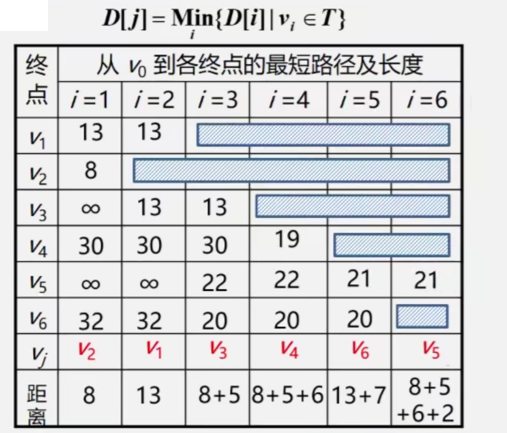
1. 将所有的顶点分为已在path的A类 和 不在path的B类 从B类中任选一个V作为初始点 V归入A类
2. 对V分别访问B类所有顶点 能直达的将距离计入数组D(下标i代表顶点编号 值代表V到D[i]的路径) 无法直达的将无穷大计入数组D
3. 对这次遍历的结果取最小值D[x]作为V到Vx的最短路径并存入数组 作为结果:第一次遍历确定了V到Vx的最短路径且值为D[x] 并将Vx归入A类 此后不再考虑Vx 因为他已进path
4. 对V分别访问B类所有顶点 如果通过Vx能到达且距离比第一次遍历结果小 将新/小距离替换旧/大距离
5. 对这次遍历的结果取最小值D[y]作为V到Vy的最短路径并存入数组 作为结果:第二次遍历确定了V到Vy的最短路径且值为D[y] 并将Vy归入A类 此后不再考虑Vy 因为他已进path
6. 依次执行2345

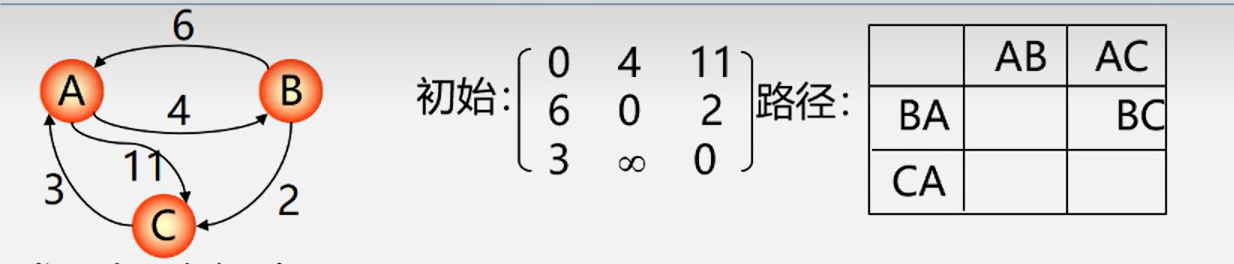
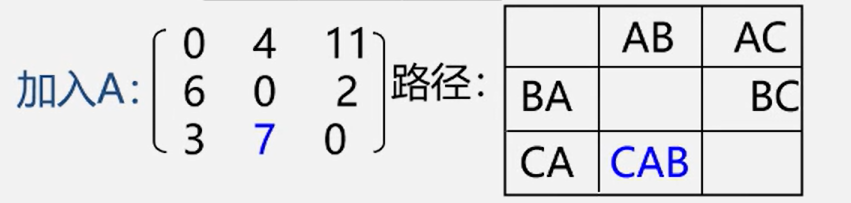
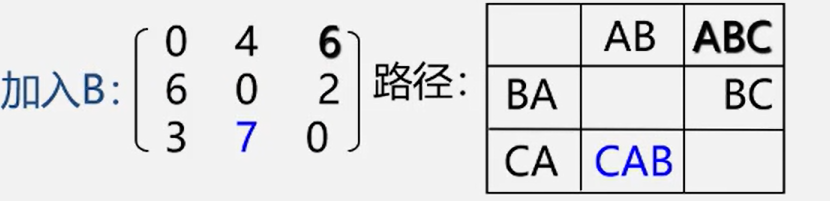
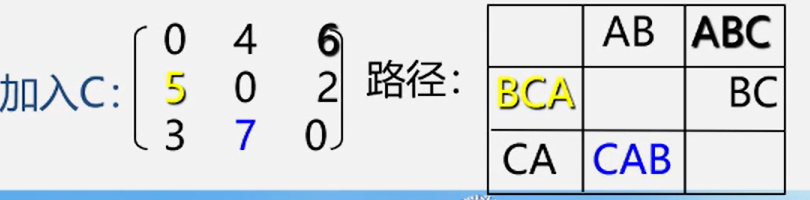
2.Floyd: 所有顶点间的最短路径

法一:Dijkstra执行n次O(N^3)

法二:Floyd (弗洛伊德)算法O(N^3)