1. 引言

  Warshall算法是一种用于求解有向图的可达矩阵的经典算法。该算法通过迭代更新图的可达矩阵，从而找到图中任意两个顶点之间的可达关系。

本文将介绍Warshall算法的实现细节，并通过一个具体的例子进行演示。

2. Warshall算法原理

  Warshall算法的核心思想是通过迭代更新矩阵，将从一个顶点到达另一个顶点的可达关系传递给整个图。算法包含两个主要步骤：

2.1 初始化可及矩阵

  遍历图的边集，根据边的关系初始化可及矩阵。如果有一条边连接顶点 Vi 和 Vj，则将可及矩阵的相应位置设为 1。

2.2 迭代更新可及矩阵

  通过三重循环嵌套，对可及矩阵进行迭代更新。如果发现存在一个顶点 Vk，使得从顶点 Vi 经过 Vk 到达顶点 Vj，则将可及矩阵中 Vi 和 Vj 之间的位置设为 1。

3. 实验内容

第一题. 实现书上 204 页的 Warshall 算法,求图 G 的可及矩阵。
（一） 输入数据
上面的邻接矩阵。
（二）输出要求

3.1 实验题目

  实现Warshall 算法, 求图的可及矩阵

（一）输入要求

{0,1,1,1,1,0,0},
{0,0,1,1,0,0,0},
{1,0,0,0,0,0,0},
{0,0,1,0,0,0,0},
{0,0,0,0,0,1,1},
{0,0,0,0,0,0,1},
{0,0,0,0,0,0,0}

（二）输出要求

1. 输出可及矩阵。
2. 输出任意两个不相邻顶点 i，j 的具体可及信息，即顶点 i，j 因为哪个顶点可及（以打印语句形式输出）。
   提示：当程序计算出某两个不相邻顶点 i，j 可及时，输出此语句，形如：“顶点 i 和顶点 j 经由顶点 v 可及。

3.2 算法实现

#include<stdio.h>
#define N 7

void Warshall(int A[][N]) {
    int B[N][N] = {0}, i, j, k, t = 0;

    // 初始化可及矩阵
    for (i = 0; i < N; i++)
        for (j = 0; j < N; j++)
            B[i][j] = (i == j) ? 1 : (A[i][j] == 1) ? 1 : 0;

    // 迭代更新可及矩阵
    for (k = 0; k < N; k++) {
        for (i = 0; i < N; i++) {
            if (B[i][k]) {
                for (j = 0; j < N; j++) {
                    t = 0;
                    if (B[i][j] == 0) t = 1;
                    B[i][j] = B[i][j] || B[k][j];
                    if (B[i][j] && t) 
                        printf("顶点%d和顶点%d经由顶点%d可及\n", i, j, k);
                }
            }
        }
    }

    // 打印可及矩阵
    printf("可及矩阵为：\n");
    for (i = 0; i < N; i++) {
        for (j = 0; j < N; j++)
            printf("%d ", B[i][j]);
        printf("\n");
    }
}

int main() {
    int A[N][N] = {
        {0, 1, 1, 1, 1, 0, 0},
        {0, 0, 1, 1, 0, 0, 0},
        {1, 0, 0, 0, 0, 0, 0},
        {0, 0, 1, 0, 0, 0, 0},
        {0, 0, 0, 0, 0, 1, 1},
        {0, 0, 0, 0, 0, 0, 1},
        {0, 0, 0, 0, 0, 0, 0}
    };
    Warshall(A);
    return 0;
}

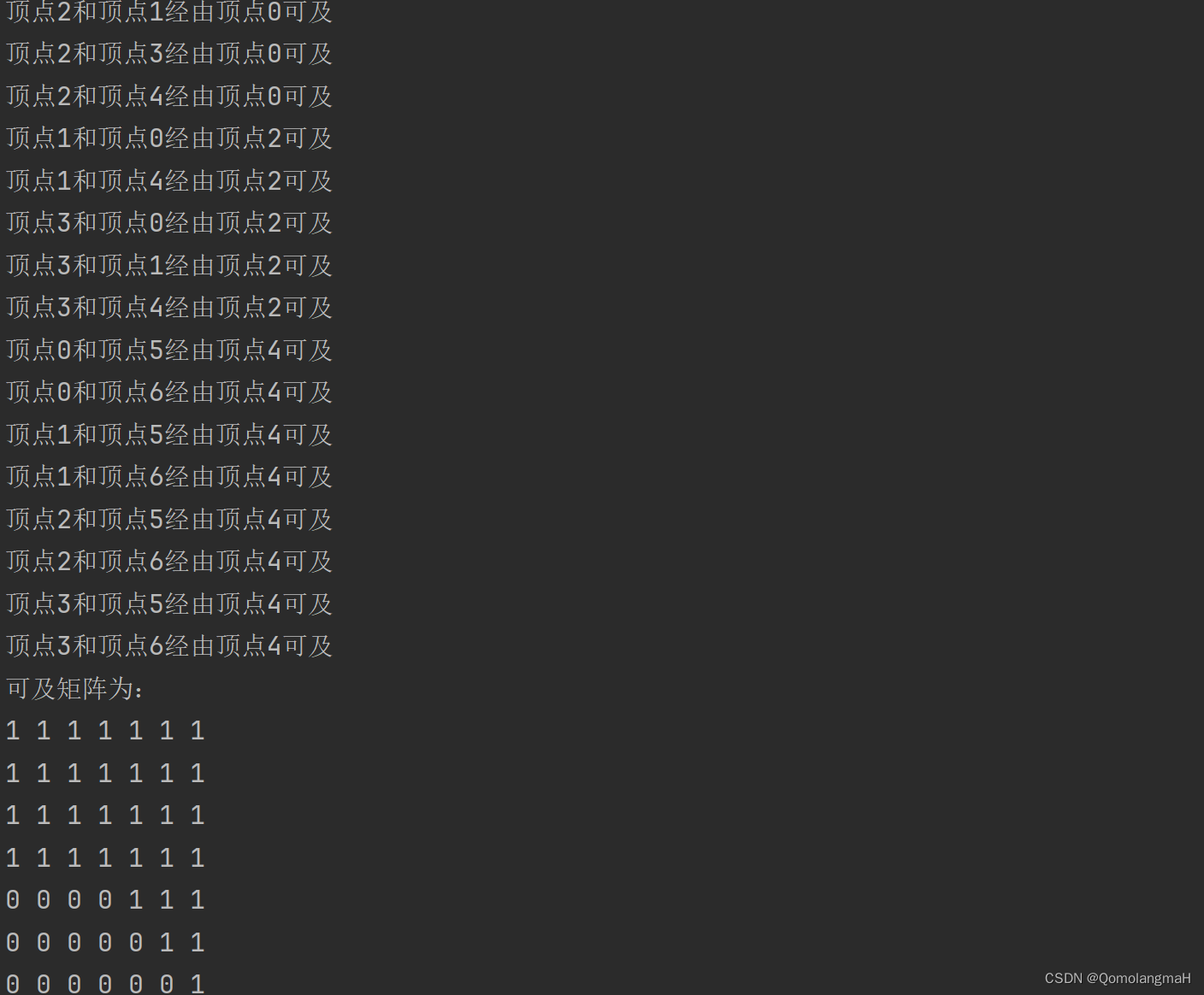
这个程序会输出可及矩阵，并在更新矩阵的过程中打印出经由哪些顶点可以到达其他顶点。

4. 实验结果