分流器
文章目录
- 分流器
- 1、概述
- 2、通用/网络配置
- 3、无功分流器
- 3.1 电阻电容分流器
- 3.2 电阻-电感分流器
- 4、总结
我们在之前关于分压器的文中已经看到,分压过程是通过在串联配置中关联相同的组件来实现的。 在本文中,我们将重点关注电流分频器执行的电流分频过程,电流分频器是组件的并行关联。
第一部分讨论了最常见的分流器类型,其最简单的形式是由两个并联的电阻器组成。
有关电阻分流器的更多配置和细节将在第二部分中讨论。
最后,以下部分介绍了部分由电抗元件制成的分流器的替代形式。
1、概述
最基本的电阻分流器配置如下图1所示:

现在我们将演示分流器公式,即 I 1 I_1 I1 和 I 2 I_2 I2 作为源 I S I_S IS 以及电阻 R 1 R_1 R1 和 R 2 R_2 R2 的函数的表达式。
首先,根据欧姆定律,我们将这两个电流表示为电压 V V V 的函数: I 1 = V / R 1 I_1=V/R_1 I1=V/R1 和 I 2 = V / R 2 I_2=V/R_2 I2=V/R2。
根据基尔霍夫电流定律,电流源可写为各支路独立电流之和: I S = I 1 + I 2 = V × ( 1 / R 1 + 1 / R 2 ) I_S=I_1+I_2=V \times (1/R_1+1/R_2) IS=I1+I2=V×(1/R1+1/R2)。
在相同分母下,该表达式变为 V = ( R 1 × R 2 / ( R 1 + R 2 ) ) × I S V=(R_1\times R_2/(R_1+R_2))×I_S V=(R1×R2/(R1+R2))×IS。 最后,我们将 I 1 I_1 I1和 I 2 I_2 I2表达式中的V代入,得到电阻分流器公式:

这些表达式中的无量纲因子范围从 0( I 1 I_1 I1 表达式中的 R 2 = 0 R_2=0 R2=0 或 I 2 I_2 I2 的 R 1 = 0 R_1=0 R1=0)到 1( I 1 I_1 I1 的 R 1 = 0 R_1=0 R1=0 和 I 2 I_2 I2 的 R 2 = 0 R_2=0 R2=0),这对于获得任何可能的输出值都很有趣 通过设置适当的电阻值,电流从 0 到 I S I_S IS。
实际上,电阻值永远不会等于 0,因为电线的电阻很小但不为零。 然而,我们仍然可以说,对于 R 1 > > R 2 R_1>>R_2 R1>>R2, I 1 = 0 I_1=0 I1=0且 I 2 = I S I_2=I_S I2=IS,对于 R 2 > > R 1 R_2>>R_1 R2>>R1, I 1 = I S I_1=I_S I1=IS且 I 2 = 0 I_2=0 I2=0。
公式1的表达式可以推广到构成分流器的任何组件,为此,我们使用阻抗形式化:

由于分流器由并联组件组成,因此通常建议使用导纳而不是阻抗以简化计算。 事实上,电阻器 R 的导纳(admittances)可写为 Y = 1 / R Y=1/R Y=1/R,在并联配置中,导纳只需相加即可: Y t o t = Y 1 + Y 2 + … Y_{tot}=Y_1+Y_2+… Ytot=Y1+Y2+…
为了说明该方法的简化改进,我们重新考虑图1中的电路,其导纳如下:

这里,等效并联导纳简单地由 Y t o t = Y 1 + Y 2 Y_{tot}=Y_1+Y_2 Ytot=Y1+Y2给出。 因此,我们有关系 V × Y t o t = I S V\times Y_{tot}=I_S V×Ytot=IS。 将式子 I 1 = V / R 1 = V × Y 1 I_1=V/R_1=V\times Y_1 I1=V/R1=V×Y1 和 I 2 = V / R 2 = V × Y 2 I_2=V/R_2=V\times Y_2 I2=V/R2=V×Y2 中的 V 代入,可得:

分流器的一个非常有用的应用是安全测量电流,同时保护测量仪器和用户。 下图 3 给出了当前测量的示例:

元件的形状决定了电阻器应采用的比例。 事实上,为了保护安培表免受高电流影响,电阻器 R2 必须高于 R1,以限制测量设备上的电流。
例如,如果源提供的电流 I S = 1 A I_S=1A IS=1A,但安培表接受的最大值为 0.05 A,我们可以选择 R 1 R_1 R1 和 R 2 R_2 R2 的值,使比率 R 1 / ( R 1 + R 2 ) R_1/(R_1+R_2) R1/(R1+R2) 等于或小于 1 /20。 例如,值 R 1 = 1 k Ω R_1=1k\Omega R1=1kΩ且 R 2 = 19 k Ω R_2=19k\Omega R2=19kΩ将满足该条件。
最后,为了向用户显示正确的值,安培表只需将测量值乘以反分数 ( R 1 + R 2 ) / R 1 (R_1+R_2)/R_1 (R1+R2)/R1。
2、通用/网络配置
通用或网络分流器配置由两个以上并联电阻器构成。 在下面的图 4 中,我们展示了具有 4 个组件的电阻网络分流器:

对于此类电路或任何由 N 个电阻组成的电流网络分压器,任何电流的通用公式由公式4 给出,其中 R e q R_{eq} Req 为并联等效电阻值。

分流器网络可用于限制输出中的电流,如图 3 中的安培表所示,此外还可以限制每个电阻器中的电流。
例如,如果我们重新考虑图 3 中给出的配置,我们可以计算每个电阻器的功耗:
- P 1 = R 1 × I 1 2 = 1000 × ( 0.95 ) 2 = 903 W P_1=R_1×I_1^2=1000×(0.95)^2=903W P1=R1×I12=1000×(0.95)2=903W
- P 2 = R 2 × I 2 2 = 1 9 × 1 0 3 × ( 0.05 ) 2 = 47 W P_2=R_2×I_2^2=1_9×10^3×(0.05)^2=47W P2=R2×I22=19×103×(0.05)2=47W
电阻器 R 1 R_1 R1 中的 900W 值显然太大,无法处理,并且会熔化电阻器结构,即使使用专门设计的高功率应用电阻器也是如此。
通过分流器网络,我们可以更均匀地分配总功率 (1000 W),并且每个电阻器的值更低。 例如,我们可以选择并联 20 个相同值 (1 kΩ) 的电阻器。 在这种情况下,每个电阻器仅吸收 0.05 A 电流并消耗 1000×(0.05)2=2.5 W 的低值,这既考虑了电阻器的条件又考虑了测量设备的保护。
3、无功分流器
考虑图2时,我们可以用电容器或电感器等电抗元件替换其中一个导纳(例如 Y 2 Y_2 Y2)。 这些可能的关联为分流器提供了交流机制中有趣的特性。
3.1 电阻电容分流器
在此配置中,电阻器与电容器并联放置,如图5所示。我们将此分流器称为 R / / C R//C R//C 关联。

可以看出,电阻器和电容器上的电流与频率相关,并且可以通过公式 5 中所示的以下关系来表示。IR 的电流表达式由广义分流器公式和 IC 的表达式通过简单地应用来获得 基尔霍夫现行定律。

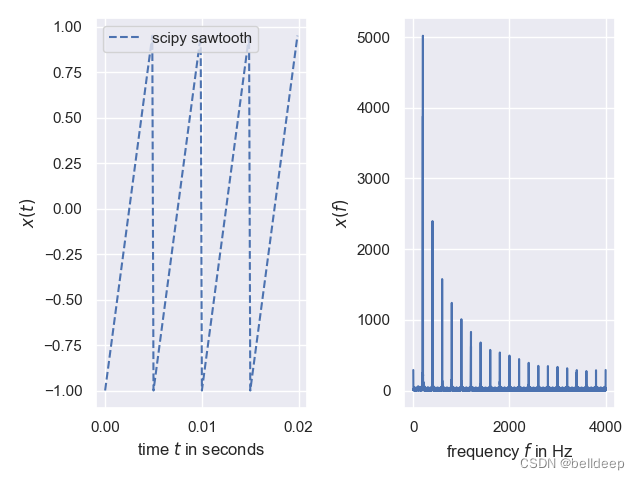
我们选择 R = 1 k Ω R=1 kΩ R=1kΩ、 C = 5 μ F C=5 μF C=5μF 和 I S = 1 A I_S=1 A IS=1A,以显示这些电流的绘图示例:

正如我们所看到的,由于电容器的电抗,电流 I C I_C IC 在低频时为零,在高频时增加直至短路。 另一方面,当源频率增加时,电阻器电流减小。 请注意, I R + I C I_R+I_C IR+IC 是常数,等于 I S = 1 A I_S=1A IS=1A。
在实践中, R / / C R//C R//C 电路用作低通滤波器,以消除输出端的高频。 此外,双极放大器中经常使用并联电容器作为耦合和去耦组件,以将不需要的高频信号缩短至接地。
3.2 电阻-电感分流器
通过并联放置的电阻器和电感器(我们称之为 R / / L R//L R//L 关联),可以制作 R / / C R//C R//C 关联的互补电路。

电流同样取决于交流电源的频率,其表达式由公式 6 给出:

我们选择 R=1 kΩ、L=5 mF 和 IS=1 A,以显示这些电流的绘图示例:

电感器的阻抗随着频率的增加而增加,因此电流IL减小。 当频率增加时,流过电阻器的电流更大。 请注意, I R + I L I_R+I_L IR+IL 是等于 I S = 1 A I_S=1A IS=1A 的常数。
实际上, R / / L R//L R//L 分流器用作高通滤波器,因为可以在电阻器支路中收集高频。 该电路是先前介绍的 R / / C R//C R//C 电路的双重电路。
4、总结
分流器是至少两个电子元件的并联组合,其将源提供的电流分成几个较小的电流。这种配置可以提供良好的电流值以匹配电路中任何级的动态。
- 在第一部分中,我们详细介绍了最常见和最简单的分流器,该分流器由两个并联电阻组成。 我们演示了电阻分流器关系并解释了电路的工作原理。 此外,还提供了另一种带有导纳的形式以及一个简单的应用示例。
- 第二部分介绍了具有两个以上电阻器的配置,这种配置有助于将电源分配到更多组件并避免发生事故。
- 最后,最后一节显示了带有无功组件的简单分流器。 由于其阻抗与频率相关,电容器和电感器可以与电阻器并联使用,以便在某些特定频率范围内分配电流。