欢迎来到Cefler的博客😁
🕌博客主页:那个传说中的man的主页
🏠个人专栏:题目解析
🌎推荐文章:题目大解析(3)

目录
- 👉🏻位图概念
- bitset
- 👉🏻位图的实现
- 将某数据在位图的某比特位置设置为1存在
- 将某数据在位图的某比特位置设置为0不存在
- 检测某某数据在位图的某比特位置是否为1
- complete code
- 👉🏻设计位图找到只出现一次的整数
- 👉🏻布隆过滤器
- 概念
- 多个哈希函数的原因:
- 布隆过滤器的查找
- 布隆过滤器删除
- 布隆过滤器优缺点
- 布隆过滤器简单实现
👉🏻位图概念
在C++中,哈希位图(Hash Bitmap)是一种数据结构,用于高效地判断一个元素是否存在于集合中。它通常用于解决查找和去重的问题。
哈希位图基于位操作实现,使用一个位数组来表示集合的元素状态。每个元素对应位数组中的一个位,如果该位被设置为1,表示该元素存在于集合中;如果该位为0,则表示该元素不存在于集合中。
哈希位图的基本思想是利用哈希函数将元素映射到位数组的索引位置。当需要插入一个元素时,先通过哈希函数计算出其对应的索引位置,在位数组中将该位设置为1。当需要查询一个元素是否存在时,同样通过哈希函数计算出索引位置,并检查位数组中对应位的值。
哈希位图的优点是占用空间较小,因为它只使用一个比特位来表示一个元素的存在与否。相比于传统的数组或链表,哈希位图在空间复杂度上更加高效。此外,哈希位图在插入、查询等操作上也具有较好的性能,时间复杂度通常为O(1)。
然而,哈希位图也存在一些限制。首先,它只适用于元素的取值范围较小且离散的情况,因为位数组的大小与元素的最大值有关。当元素取值范围较大时,位数组的空间消耗也会增加。其次,哈希函数的选择对于哈希位图的性能影响较大,一个好的哈希函数应该能够均匀地将元素分布到位数组中。
总的来说,哈希位图是一种高效的数据结构,适用于解决查找和去重问题,它在空间和时间复杂度上都具有优势。
bitset
C++ 的 <bitset> 头文件提供了 std::bitset 类,用于表示固定大小的位集合(bit set)。std::bitset 是一个固定大小的位数组,其中的每一位都可以被设置或清除,也可以进行位运算操作。以下是 bitset 头文件的主要用法:
创建和初始化 bitset:
#include <bitset>
#include <iostream>
int main() {
// 创建一个包含 8 位的位集合,所有位初始化为 0
std::bitset<8> bits1;
// 使用整数初始化位集合
std::bitset<8> bits2(255); // 255的二进制表示为 "11111111"
// 使用二进制字符串初始化位集合
std::bitset<8> bits3("10101010");
std::cout << "bits1: " << bits1 << std::endl;
std::cout << "bits2: " << bits2 << std::endl;
std::cout << "bits3: " << bits3 << std::endl;
return 0;
}
访问和修改位:
std::bitset<8> bits("11001100");
// 访问位
bool bit5 = bits[5]; // 获取第 5 位的值
// 修改位
bits.set(3, 1); // 将第 3 位设置为 1
bits.reset(2); // 将第 2 位设置为 0
bits.flip(1); // 将第 1 位取反
std::cout << "bits: " << bits << std::endl;
位运算操作:
std::bitset<4> bits1("1010");
std::bitset<4> bits2("0110");
// 位与运算
std::bitset<4> result_and = bits1 & bits2; // 结果为 "0010"
// 位或运算
std::bitset<4> result_or = bits1 | bits2; // 结果为 "1110"
// 位异或运算
std::bitset<4> result_xor = bits1 ^ bits2; // 结果为 "1100"
std::cout << "AND: " << result_and << std::endl;
std::cout << "OR: " << result_or << std::endl;
std::cout << "XOR: " << result_xor << std::endl;
其他操作:
std::bitset<8> bits("11001100");
// 统计位集合中设置为 1 的位数
std::cout << "Count of 1s: " << bits.count() << std::endl;
// 测试某一位是否为 1
bool test_result = bits.test(3); // 测试第 3 位是否为 1
// 找到第一个被设置为 1 的位的位置
size_t first_set_bit = bits._Find_first();
std::cout << "Test result: " << test_result << std::endl;
std::cout << "First set bit: " << first_set_bit << std::endl;
这只是 std::bitset 的一些基本用法,还有其他方法和操作可供使用。 bitset 是一个非常方便的工具,特别适用于需要高效表示和操作位信息的场景。
👉🏻位图的实现
将某数据在位图的某比特位置设置为1存在
void set(const int& x)
{
int i = x / 32;//在位图中的第i个整型
int j = x % 32;//bit位
_bits[i] |= (1 << j);
}
将某数据在位图的某比特位置设置为0不存在
void reset(const int& x)
{
int i = x / 32;
int j = x % 32;
_bits[i] &= ~(1 << j);
}
检测某某数据在位图的某比特位置是否为1
bool test(const int& x)
{
int i = x / 32;
int j = x % 32;
return _bits[i] & (1 << j);
}
complete code
#include<iostream>
#include<vector>
using namespace std;
namespace bit
{
template<size_t N>
class bitset
{
public:
void set(const int& x)
{
int i = x / 32;//在位图中的第i个整型
int j = x % 32;//bit位
_bits[i] |= (1 << j);
}
//将某数据在位图的某比特位置设置为0不存在
void reset(const int& x)
{
int i = x / 32;
int j = x % 32;
_bits[i] &= ~(1 << j);
}
bool test(const int& x)
{
int i = x / 32;
int j = x % 32;
return _bits[i] & (1 << j);
}
private:
vector<int> _bits;
};
}
👉🏻设计位图找到只出现一次的整数
#include<iostream>
#include<vector>
using namespace std;
namespace bit
{
template<size_t N>
class bitset
{
public:
void set(const int& x)
{
int i = x / 32;//在位图中的第i个整型
int j = x % 32;//bit位
_bits[i] |= (1 << j);
}
//将某数据在位图的某比特位置设置为0不存在
void reset(const int& x)
{
int i = x / 32;
int j = x % 32;
_bits[i] &= ~(1 << j);
}
bool test(const int& x)
{
int i = x / 32;
int j = x % 32;
return _bits[i] & (1 << j);
}
private:
vector<int> _bits;
};
template<size_t N>
class twobitset
{
public:
void set(size_t x)
{
//00->01
//01->10
//10->11
//11->不变
if (_bs1.test(x) == false && _bs2.test(x) == false)
{
_bs2.set(x);
}
else if (_bs1.test(x) == false && _bs2.test(x) == true)
{
_bs1.set(x);
_bs2.reset(x);
}
else if (_bs1.test(x) == true && _bs2.test(x) == false)
{
_bs1.set(x);
_bs2.set(x);
}
}
void Print()
{
for (size_t i = 0; i < N; i++)
{
if (_bs1.test(i) == false && _bs2.test(i) == true)
{
cout <<"1->" << i << endl;
}
else if (_bs1.test(i) == true && _bs2.test(i) == false)
{
cout <<"2->" << i << endl;
}
}
cout << endl;
}
private:
bitset<N> _bs1;
bitset<N> _bs2;
};
}
👉🏻布隆过滤器
概念
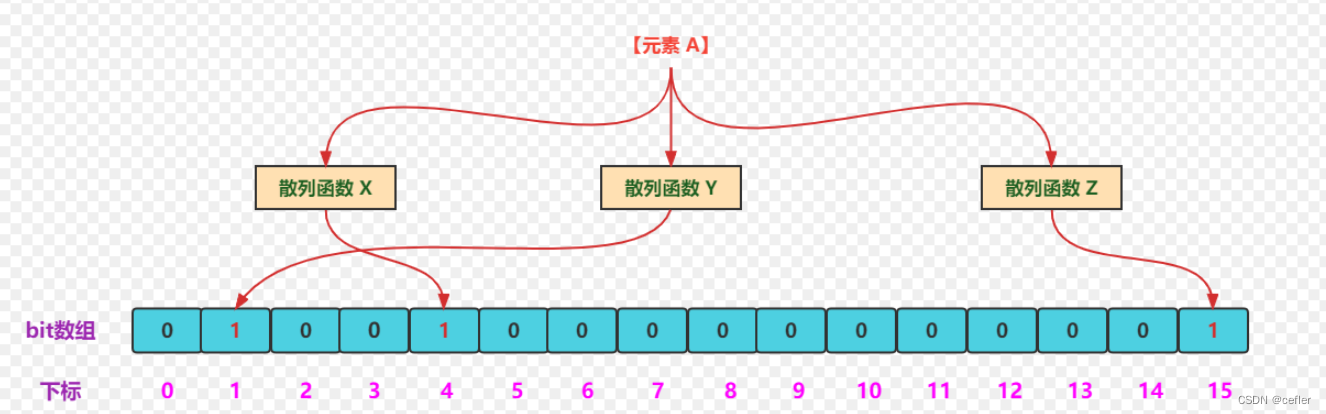
布隆过滤器是一种用于判断一个元素是否属于一个集合的概率型数据结构。它在解决大规模数据集合的查找问题上具有一些优势,但也有一些局限性。以下是布隆过滤器存在的主要意义:
意义 :
-
高效的查找操作: 布隆过滤器可以快速判断一个元素是否属于集合,而无需存储实际的元素信息。这使得在大规模数据集合中进行查找操作更为高效。
-
节省内存: 布隆过滤器相对于其他数据结构来说,具有较小的内存占用。这是因为它不需要存储实际元素,只需维护一个位数组即可。
-
快速插入和删除: 布隆过滤器的插入和删除操作是常数时间复杂度,这使得它在某些场景下比其他数据结构更为高效。
注意!
布隆过滤器,可以用来告诉你 “某样东西一定不存在或者可能存在”
多个哈希函数的原因:
-
减少碰撞(冲突)的概率: 哈希函数的目标是将元素均匀地映射到位数组的不同位置。使用多个哈希函数可以减少碰撞的概率,即不同元素映射到相同位置的可能性。
-
降低误判率: 布隆过滤器的主要缺点是可能存在误判(false positives),即判断元素存在于集合中,但实际上并不存在。使用多个哈希函数可以降低这种误判的概率,提高布隆过滤器的准确性。
-
增强抗攻击性: 多个哈希函数可以增加布隆过滤器对恶意攻击(例如故意构造冲突以使过滤器失效)的抵抗力。
虽然使用多个哈希函数能够提高布隆过滤器的性能和准确性,但也需要权衡计算成本。因为每个哈希函数都需要计算,使用太多哈希函数可能会降低性能,因此选择适量的哈希函数是一项需要仔细考虑的任务。
布隆过滤器的查找
布隆过滤器的查找操作主要用于判断一个元素是否可能存在于集合中。请注意,布隆过滤器存在一定的误判率(false positive),即它可能错误地认为元素存在于集合中,但实际上并不存在。
下面是布隆过滤器的查找过程:
-
哈希函数: 首先,将要查找的元素通过多个哈希函数映射到位数组中的多个位置。这些哈希函数应该是独立且均匀分布的,以减小碰撞的概率。
-
检查位数组: 对应于这些哈希函数映射的位数组位置上的位,如果所有的位都被设置为1,那么布隆过滤器判定元素可能存在于集合中。
-
判断结果: 如果所有对应位置的位都是1,那么布隆过滤器返回一个“可能存在”的结果,表示元素可能存在于集合中。否则,它确定元素一定不存在于集合中。
需要注意的是,如果查找结果是“可能存在”,那么还需要进一步的验证,例如在一个真正的数据存储结构(服务器)中进行实际查找,以确认元素是否确实存在。
由于布隆过滤器的误判率,它适合用于那些对于少数误判可以容忍的场景,例如缓存、防止数据库查询等。然而,在要求绝对准确性的场景下,不适合使用布隆过滤器。
布隆过滤器删除
布隆过滤器(Bloom Filter)是一种设计用来加速元素是否存在于集合中的数据结构,但它不支持直接删除元素。这是因为删除元素可能影响到其他元素的映射,从而导致不准确的结果。
具体来说,如果要删除布隆过滤器中的某个元素,会涉及将元素对应的位数组位置重置为0。然而,这会影响到其他元素,因为可能存在多个元素映射到同一个位数组位置。如果重置一个位,可能会使其他元素的对应位也被重置,从而导致误判。
布隆过滤器优缺点
布隆过滤器(Bloom Filter)是一种用于加速元素是否存在于集合中的数据结构,具有一些明显的优点和一些局限性。以下是布隆过滤器的主要优缺点:
优点:
-
快速查询: 布隆过滤器在判断元素是否存在于集合中的查询操作上非常高效,通常为常数时间复杂度。
-
节省内存: 相对于一些其他数据结构(比如哈希表),布隆过滤器使用的内存较少,因为它只需要维护一个位数组,而不需要存储实际的元素信息。
-
高效的插入和删除: 插入和删除操作都是常数时间复杂度,使得布隆过滤器在某些特定场景下比其他数据结构更高效。
缺点 :
-
误判率: 布隆过滤器存在一定的误判率,即可能会将不存在于集合中的元素错误地判断为存在。这是由于多个元素映射到同一位置可能导致的冲突。
-
不支持删除: 布隆过滤器不支持直接删除元素。删除元素可能会影响其他元素的映射,导致不准确的结果。
-
哈希函数的选择: 布隆过滤器的性能与所选择的哈希函数密切相关。选择不好的哈希函数可能会增加误判率。
-
固定大小: 布隆过滤器的大小是固定的,不能动态调整。如果元素数量超过预期,可能需要重新设计和调整布隆过滤器的大小。
-
不适用于小数据集: 在小数据集上,误判率相对较高,因此布隆过滤器可能不是最佳选择。
总体来说,布隆过滤器适用于那些对于一定的误判可以容忍的大规模数据集合查询场景,但在对精确性要求高、数据集规模较小或者需要频繁插入和删除元素的场景中可能不合适。
布隆过滤器简单实现
C++中,你可以使用标准库中的 std::bitset 或者其他哈希库来实现布隆过滤器。
以下是一个简单的C++布隆过滤器的实现示例:
#include <bitset>
#include <functional>
#include <iostream>
class BloomFilter {
public:
BloomFilter(int size)
: size(size)
{
filter.reset();
}
// 添加元素
void add(const std::string& element) {
for (auto& hashFunction : hashFunctions) {
std::size_t hash = hashFunction(element);
filter.set(hash % size, true);
}
}
// 检查元素是否存在于集合中
bool contains(const std::string& element) const {
for (auto& hashFunction : hashFunctions) {
std::size_t hash = hashFunction(element);
if (!filter.test(hash % size)) {
return false;
}
}
return true;
}
private:
int size;
std::bitset<1000> filter; // 用于存储数据的位集合,根据实际需要调整大小
std::hash<std::string> hashFunction1;
std::hash<std::string> hashFunction2;
// 可以添加更多的哈希函数
std::hash<std::string> hashFunctions[2] = {hashFunction1, hashFunction2};
};
int main() {
BloomFilter bloomFilter(1000);
bloomFilter.add("example");
bloomFilter.add("test");
std::cout << "Contains 'example': " << bloomFilter.contains("example") << std::endl; // 输出 1 (true)
std::cout << "Contains 'hello': " << bloomFilter.contains("hello") << std::endl; // 输出 0 (false)
return 0;
}
上述示例中,BloomFilter 类有一个位集合(用 std::bitset 实现),并使用两个哈希函数来将元素映射到位集合中。你可以根据需要添加更多的哈希函数。 add 方法用于添加元素,而 contains 方法用于检查元素是否可能在集合中。
如上便是本期的所有内容了,如果喜欢并觉得有帮助的话,希望可以博个点赞+收藏+关注🌹🌹🌹❤️ 🧡 💛,学海无涯苦作舟,愿与君一起共勉成长