在现代科学和工程领域,曲线拟合是一项重要的数据分析技术,它可以通过数学模型来近似描述实际数据中的复杂关系。本文将详细介绍曲线拟合的基本概念、方法和应用领域,并探究其在数据建模中的艺术与科学。
第一节:曲线拟合的基本概念和目标
曲线拟合是一种利用数学函数模拟现实世界中数据关系的方法。其基本目标是通过寻找最佳的曲线来连接已知数据点或逼近未知数据,以获取对数据背后关系的了解。曲线拟合能够使数据更加直观、可视化,并为进一步分析和预测提供基础。

第二节:常见的曲线拟合方法
1. 最小二乘法:最小二乘法是一种常用的曲线拟合方法,其原理是寻找使拟合曲线与实际数据之间误差平方和最小的参数。这种方法适用于线性和非线性模型,并且可以通过调整参数的选择,使得拟合结果更加准确。
2. 多项式拟合:多项式拟合是一种将数据拟合为多项式函数的方法。通过增加多项式的阶数,可以使拟合曲线更加复杂,更好地逼近数据。然而,高阶多项式容易发生过拟合现象,因此选择适当的多项式阶数很关键。
3. 样条插值:样条插值是一种基于数据点之间的插值方法,通过在给定数据点间插入光滑的样条曲线来拟合数据。这种方法在保持数据的光滑性和连续性方面非常有效。
第三节:曲线拟合的应用领域
1. 自然科学:在物理学、化学、生物学等领域中,曲线拟合广泛应用于分析实验数据、建立物理模型和研究物质性质。通过曲线拟合,科学家可以从有限的实验数据中提取出对问题的深刻见解。
2. 工程技术:在工程领域中,曲线拟合用于建立模型、预测趋势和控制系统。例如,曲线拟合可以帮助工程师分析传感器数据、优化生产过程,并预测设备的寿命和故障。
3. 金融与经济:曲线拟合在金融和经济学中用于优化投资组合、分析经济趋势和预测市场行为。通过曲线拟合,分析师可以找到数学模型来描述价格变化、收益率和风险关系。
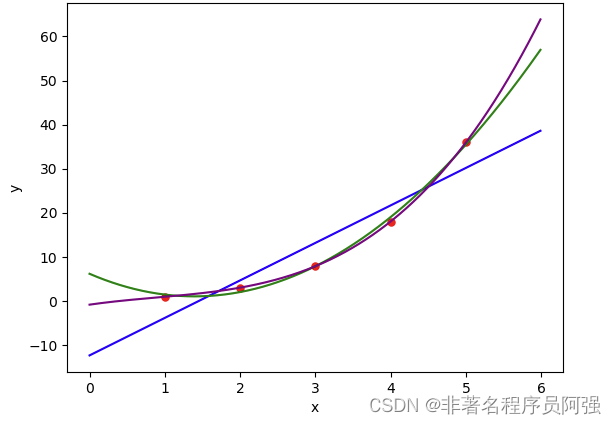
第四节:曲线拟合的艺术与科学
曲线拟合不仅仅是一项科学技术,它也融合了艺术的因素。在实际应用中,选择适当的拟合方法和合适的参数调整需要丰富的经验和直觉。同时,艺术的美感和直觉也影响着拟合结果的评估和选择,以使得曲线拟合更符合实际应用的需要。
结论:
曲线拟合作为一种重要的数据分析技术,在科学研究和实际应用中发挥着重要作用。通过曲线拟合,我们可以深入理解数据背后的关系,并通过数学模型来预测和优化系统。然而,曲线拟合既是一门科学技术,也是一门艺术,需要结合优秀的计算能力、统计知识和直觉判断。进一步研究和发展曲线拟合方法,将有助于推动数据建模领域的进步,并引领我们更深入地探索数据背后的奥秘。
人工智能的学习之路非常漫长,不少人因为学习路线不对或者学习内容不够专业而举步难行。不过别担心,我为大家整理了一份600多G的学习资源,基本上涵盖了人工智能学习的所有内容。点击下方链接,0元进群领取学习资源,让你的学习之路更加顺畅!记得点赞、关注、收藏、转发哦!扫码进群领资料