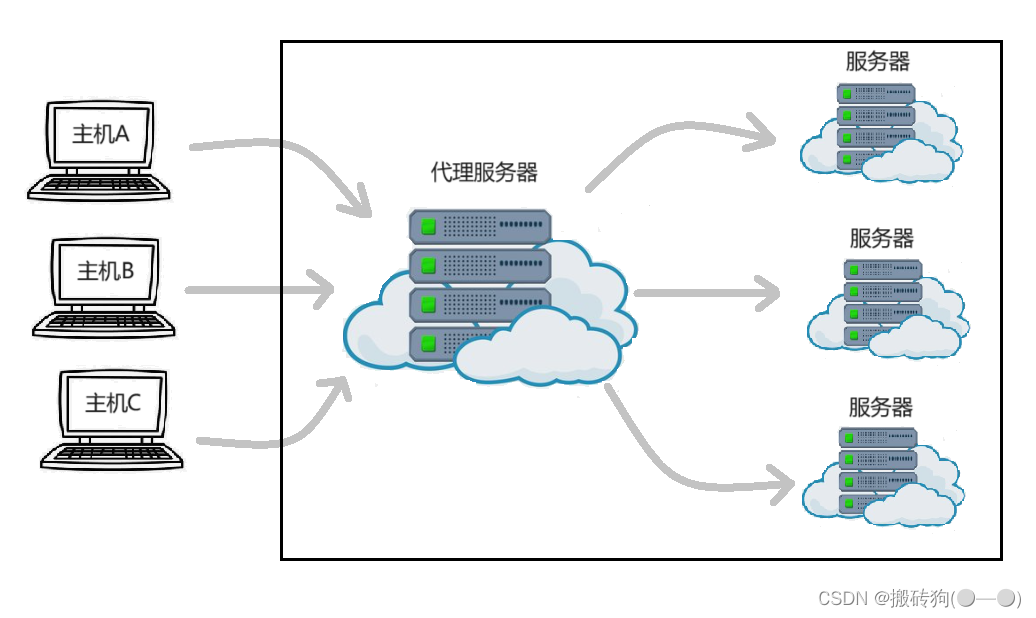
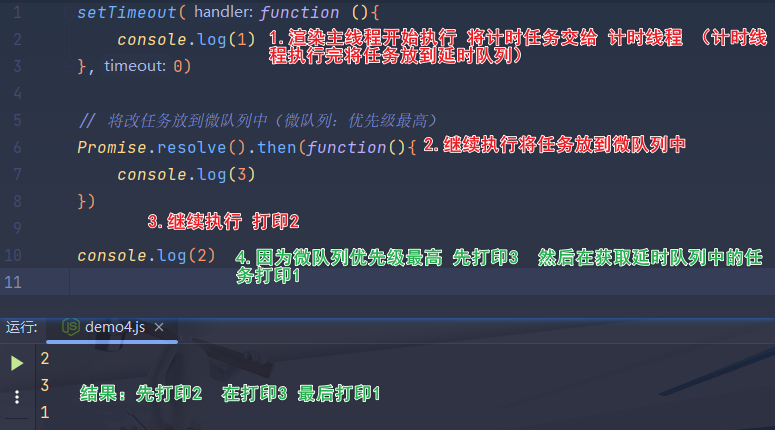
希尔伯特变换（hilbert transform）简介

在信号处理中我们常见的有傅里叶变换，用来分析频域信息，还有拉普拉斯变换和z变换，用于系统分析系统响应。短时傅里叶分析和小波分析用于时频分析。希尔伯特变换似乎听到的比较少。我因为最近在做信号幅度提取的时候看到可以用希尔伯特变换来提取包络，所以才了解到了希尔伯特变换，网上的资料很多，对它的介绍也很多，我对它的了解有限，只是知道它可以做IQ调制，也可以提取信号分包络。我觉得作为工科生，就应该本着实用主义的原则，很多公式和定理的证明是数学家的事情，我们只需要懂怎么用，把这些已有的信号处理的工具用好就行了。写这篇博客主要是为了总结、归纳和记录，如果能够恰好帮助到需要的朋友，那就更好了。
严谨一点，还是先给出公式吧。希尔伯特的数学定义如下：
设有一个实值函数$x(t)$，其希尔伯特变换记作$X(t)$
$$X(t)=H[x(t)]=\frac{1}{\pi }{\int }_{-\infty }^{\infty }\frac{x(\tau )}{t-\tau }d\tau$$
通过上面的式子可以看出来，其实希尔伯特变换就是对信号做了一下卷积，这个被卷积的信号的单位脉冲响应为：
$$h(t)=\frac{1}{\pi t}$$
我们都知道，时域做卷积，相当于对信号进行滤波，而这个滤波器的响应函数就是上面的$h(t)$。
我们对$h(t)$做傅里叶变换，可以得到：
$$H(j\omega )=-jsgn(\omega )$$
$sgn(\cdot )$函数是符号函数，也就是说这个滤波器对原始信号的正频率部分进行了$-\pi /2$的相移，而对负频率部分进行了$\pi /2$的相移。
希尔伯特变换的本质就是进行了一种特殊的卷积。

matlab希尔伯特变换函数

在matlab中，实现希尔伯特变换也是非常的简单，只需要一行代码y=hilbert(x)，我们要搞懂它的输入输出是什么，首先要知道它的输入信号必须得是实数类型的，希尔伯特变换的实部和虚部仅仅是相位差$\pi /2$，希尔伯特变换的幅度即为信号的包络，对于正弦波而言那就是一条直线，下面是一个简单的仿真：

%% 希尔伯特变换仿真
% 主要内容：点频信号生成、希尔伯特变换
% Author: huasir 2023.11.25
fs = 20e3; % 采样频率；
dt = 1/fs; %采样时间间隔
fc = 1e3; %频率
T = 10e-3;
t = 0:dt:T-dt;
x = cos(2*pi*fc*t); %生成正弦波信号
X = hilbert(x); %对x进行希尔伯特变换
%% 分别绘制正弦信号、希尔伯特变换的实部、虚部、幅度
figure;
subplot(3,1,1);
plot(t,x,t,imag(X));
legend('x','imag(X)');
xlabel('t/s');
title('原始信号和希尔伯特变换的虚部')
subplot(3,1,2);
plot(t,real(X));
legend('real(X)');
xlabel('t/s');
title('希尔伯特变换的实部')
subplot(3,1,3);
plot(t,x,t,abs(X));
legend('abs(X)');
xlabel('t/s');
title('原始信号和希尔伯特变换的幅度')

绘制出的图像如下：

图1 希尔伯特变换结果

由上图也验证了希尔伯特变换的效果，它的幅度就是信号的包络，我们可以通过这个方法进行包络提取；

下面是一个调幅信号采用希尔伯特变换进行包络提取的例子

%% 希尔伯特变换仿真
% 主要内容：调幅生成、希尔伯特变换
% Author: huasir 2023.11.25@BeiJing
fs = 100e3; % 采样频率；
dt = 1/fs; %采样时间间隔
fc = 10e3; %载波频率
f = 100; %调制信号
T = 10e-3;
t = 0:dt:T-dt;
x = cos(2*pi*fc*t).*cos(2*pi*f*t); %生成正弦波信号
X = hilbert(x); %对x进行希尔伯特变换
%% 分别绘制正弦信号、希尔伯特变换的实部、虚部、幅度
figure;
subplot(2,1,1);
plot(t,x,t,imag(X));
legend('x','imag(X)');
xlabel('t/s');
title('原始信号和希尔伯特变换的虚部')
subplot(2,1,2);
plot(t,real(X));
legend('real(X)');
xlabel('t/s');
title('希尔伯特变换的实部')
figure;
plot(t,x,t,[1;-1]*abs(X));
legend('x','abs(X)');
xlabel('t/s');
title('原始信号和包络')

输出图像入下：

图2 调幅信号希尔伯特变换的实部和虚部

图3 调幅信号采用希尔伯特变换的包络提取