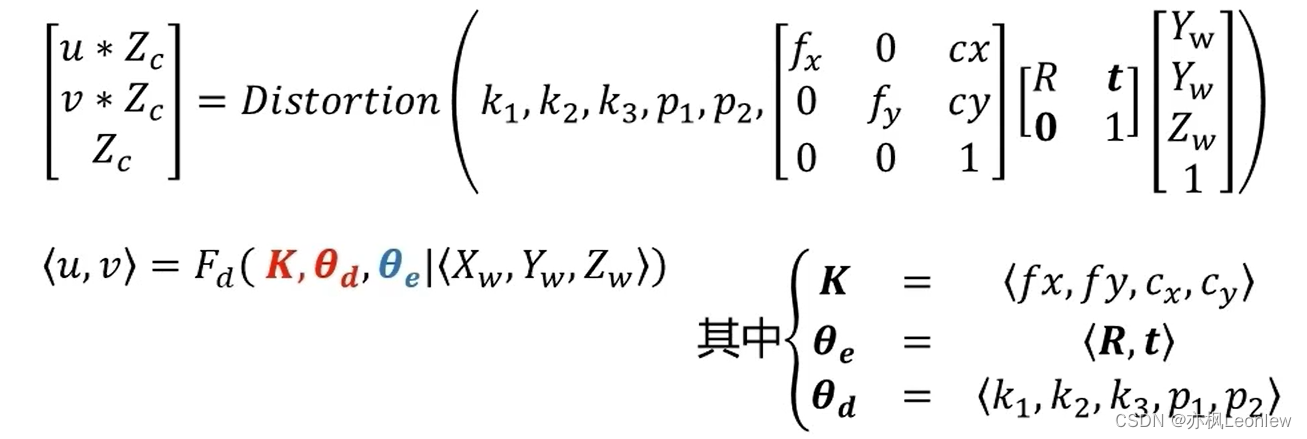什么需要相机标定
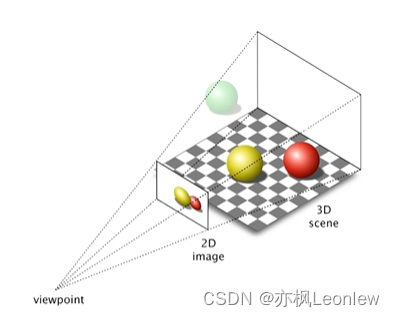
我们知道,相机的图像是三维世界到2D平面的一个投影。仅从这个2D图像来看,我们无法得知图像中的物体在真实物理世界中有多大,距离相机的距离有多远。那么我们有没有办法从这个2D的图片结合相机的参数获得这些信息呢?答案是有的,方法有很多种,比如双目视觉技术,可以用来恢复三维信息。
如何恢复精确的3D物体?图像失真(比如镜头畸变)了如何恢复?
先用数学表达式描述对相机成像过程建模,然后通过数学表达式计算恢复这些信息。
相机标定主要解决的问题
确定世界坐标系下三维空间点与像素平面像素点之间的转换关系(内参,外参)
确定相机成像过程中的畸变系数,用作图像校正
相机模型
镜头
镜头一般是由多片透镜组成,里面会有凹透镜、凸透镜等多种透镜,结构复杂。但在实际分析中,我们会将镜头做等效分析,将复杂的透镜组等效为一个凸透镜,对光线有汇聚作用。因此,先来看凸透镜的一些基本知识点。
薄凸透镜
边缘薄中间厚,对光线有汇聚作用。
主光轴: 过透镜两个表面曲率中心的直线。
光心:薄透镜的中心(厚度趋于0时,两个表面顶点重合于光心)
特点:1. 经过物点,平行于光轴的光线,经过凸透镜后,会经过焦点
2. 经过物点和光心的光线,经过凸透镜后,方向不变
3. 经过物点和物体侧焦点的光线,经过凸透镜后,平行于光轴射出
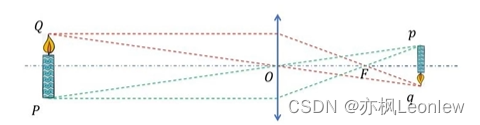
上图中,Q点和P点这两点,实际上有多条光线发出。为了简化相机成像过程,我们用通过光心的光路来代表成像光路,如下图所示:
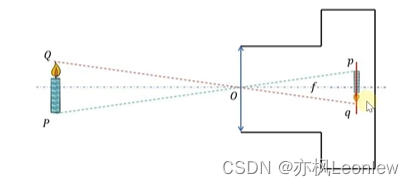
但这个简化过程需要做几个假设:
1. 假设没有像差;2. 不考虑景深(能够在成像面上清晰成像);3. 透镜为一个薄凸透镜
这种简化的相机成像模型称为针孔相机模型
成像过程中的坐标系及坐标系转换
关于本小节,在“几何角度理解相机成像过程”的笔记中已经有了描述,链接如下:
几何角度理解相机成像过程_亦枫Leonlew的博客-CSDN博客本笔记从几何角度来理解相机的成像过程,我们生活在三维世界中,相机所捕捉到的画面是2D的,3D空间中的点是如何投影到2D平面的过程是本笔记关注的。这个过程其实和3D游戏中的透视投影过程是一样的。本笔记只要知道矩阵乘法的知识就可以理解。https://blog.csdn.net/vivo01/article/details/128252788?spm=1001.2014.3001.5502
这里只复习一下几个要点。
世界坐标系:以被测物体的点作为参考定义的绝对坐标系。坐标记为(Xw,Yw,Zw)。
相机坐标系:以相机光心为坐标原点,主光轴物方交点方向为z轴,平行于(虚拟)成像平面的两条垂直边分别为x和y轴。坐标记为(Xc,Yc,Zc)。
图像坐标系:以主光轴与(虚拟)成像平面的交点为坐标原点,平行于(虚拟)成像平面的两条垂直边分别为x和y轴。坐标记为(x,y)。
像素坐标系:以(虚拟)成像平面左上角顶点为原点,u和v轴平行于图像系的x和y轴,以像素为单位。坐标记为(u,v)。
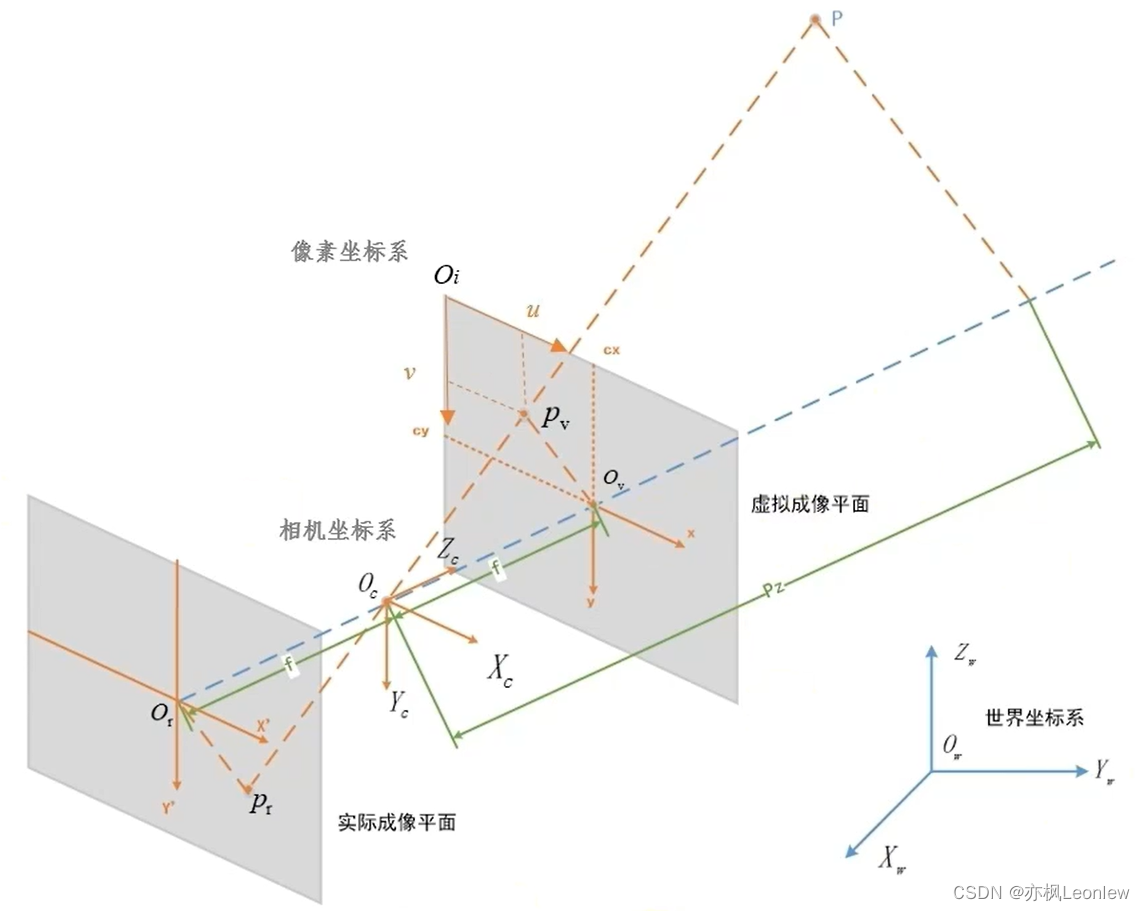
为什么引入虚拟成像面?以点P为例,其在实际成像面上的坐标和虚拟成像面的坐标是反的,虚拟成像面上的点Pv方向和世界坐标系上的方向是一致的,而实际成像面上的点Pr是倒置的。引入虚拟成像面后,在计算坐标系转换和投影时,就不用考虑符号问题了。

镜头畸变
畸变原因:理想的成像点与实际成像点并不重合,存在像差。畸变是单色光学像差中的一种,也是唯一不会改变成像清晰度的像差(球面相差就会改变图像清晰度)。
不同波长的光畸变曲线不同。透镜的畸变主要分为径向畸变和切向畸变。
径向畸变
一般分为:枕形畸变(正畸变)和桶形畸变(负畸变)
越向透镜边缘移动,径向畸变越严重,呈中心对称

这里的正和负的意思,是指理论像高和实际像高之间的差值正负,如上图所示。
切向畸变
由于透镜和sensor之间安装位置误差,导致透镜和成像平面无法严格做到平行所引发的畸变。一般是由于工艺导致。
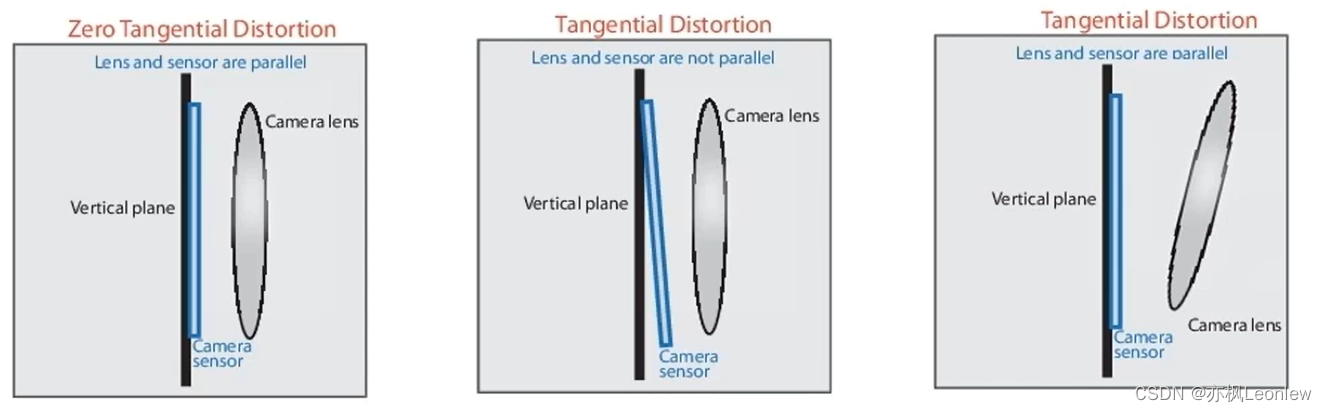
上图,从左到右分别是无切向畸变、sensor位置误差导致的切向畸变和镜头位置误差导致的切向畸变。
畸变数学模型
径向畸变模型(k3为例,opencv中会用到k6)
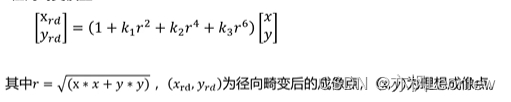
切向畸变模型

径向畸变和切向畸变模型合并
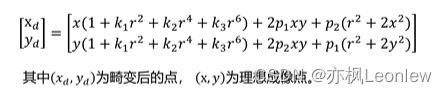
注意,为了消除畸变系数的尺度因子,坐标点和r规定是在单位焦平面上的坐标。单位焦平面是指f=1时的物方焦平面。
标定建模
数学模型
结合针孔相机模型 + 镜头畸变,相机标定模型的建立过程:
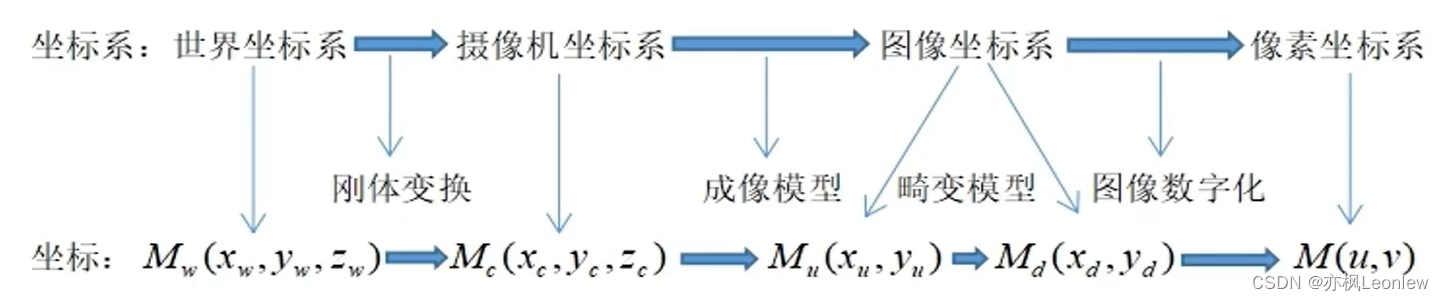
标定的数学模型