前言

随着大模型的发展，模型参数量暴涨，以Transformer的为组成成分的隐藏神经元数量增长的越来越多。因此，降低前馈层的推理成本逐渐进入视野。前段时间看到本文介绍的相关工作还是MNIST数据集上的实验，现在这个工作推进到BERT上面来了，再次引起兴趣记录一下。该工作将前馈神经基于二叉树结构进行改装，加速前向传播的速度，称为：快速前馈网络（FFF），然后应用FFF，取代BERT中的前馈网络（FF），实现12个神经元加速推理。

快速前馈网络算法概述

快速前馈网络（Fast Feedforward Network，FFF）是由两部分组成的：节点网络集合 $\mathcal{N}$ 和叶子网络集合 $\mathcal{L}$。

• 节点网络集合 $\mathcal{N}$ 包含了一组节点网络，每个节点网络都是一个 $⟨{\dim }_I,n,1⟩$-前馈网络，并在输出上增加了一个 sigmoid 激活函数。这些节点网络按照平衡的可微分二叉树的形式排列，其中 $N_{m+1,2n}$ 和 $N_{m+1,2n+1}$ 是 $N_{m,n}$ 的子节点。

• 叶子网络集合 $\mathcal{L}$ 包含了一组叶子网络，每个叶子网络都是一个 $⟨{\dim }_I,\ell ,{\dim }_O⟩$-前馈网络。叶子网络没有子节点，它们的输出直接作为 FFF 的输出。

前向传播过程由下面算法控制。

算法的输入包括一个输入样本 $\iota$ 和根节点 $N_{0,0}$，输出为该样本在 FFF 中的输出。

算法定义了两个函数：$Forwar{d}_T$ 和 ${Forward}_I$。其中，${Forward}_T$ 函数用于计算节点的输出，而 ${Forward}_I$ 函数用于计算节点的指示值（indicator value）。

• 在 ${Forward}_T$ 函数中，如果当前节点是叶子节点，则直接调用该节点的前馈传播函数 $N_{m,n}(\iota )$ 来计算输出。否则，首先计算当前节点的输出 $c_{m,n}=N_{m,n}(\iota )$，然后递归地调用 ${Forward}_T$ 函数来计算当前节点的两个子节点的输出，并将它们加权相加作为当前节点的输出。
• 在 ${Forward}_I$ 函数中，如果当前节点是叶子节点，则直接调用该节点的前馈传播函数 $N_{m,n}(\iota )$ 来计算输出。否则，首先计算当前节点的输出 $c_{m,n}=N_{m,n}(\iota )$，然后根据输出值的大小决定选择哪个子节点进行递归计算。

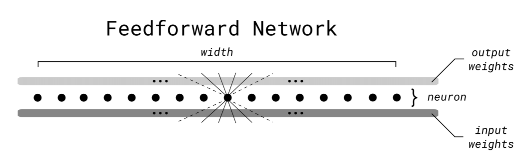
传统前馈神经网络

快速前馈神经网络

与传统的前馈神经网络算法相比，该算法的主要区别在于引入了一个计算节点的指示值。指示值表示了当前节点的输出是否大于等于阈值（这里的阈值为0.5），根据指示值的大小来确定选择哪个子节点进行计算。这种方式可以大大减少计算量，提高前向传播的效率。同时，FFF 是一种具有平衡二叉树结构的前馈神经网络，其中节点网络和叶子网络分别用于处理中间层和输出层的计算。通过利用二叉树结构和递归计算，FFF 可以实现快速的前向传播。

UltraFastBERT

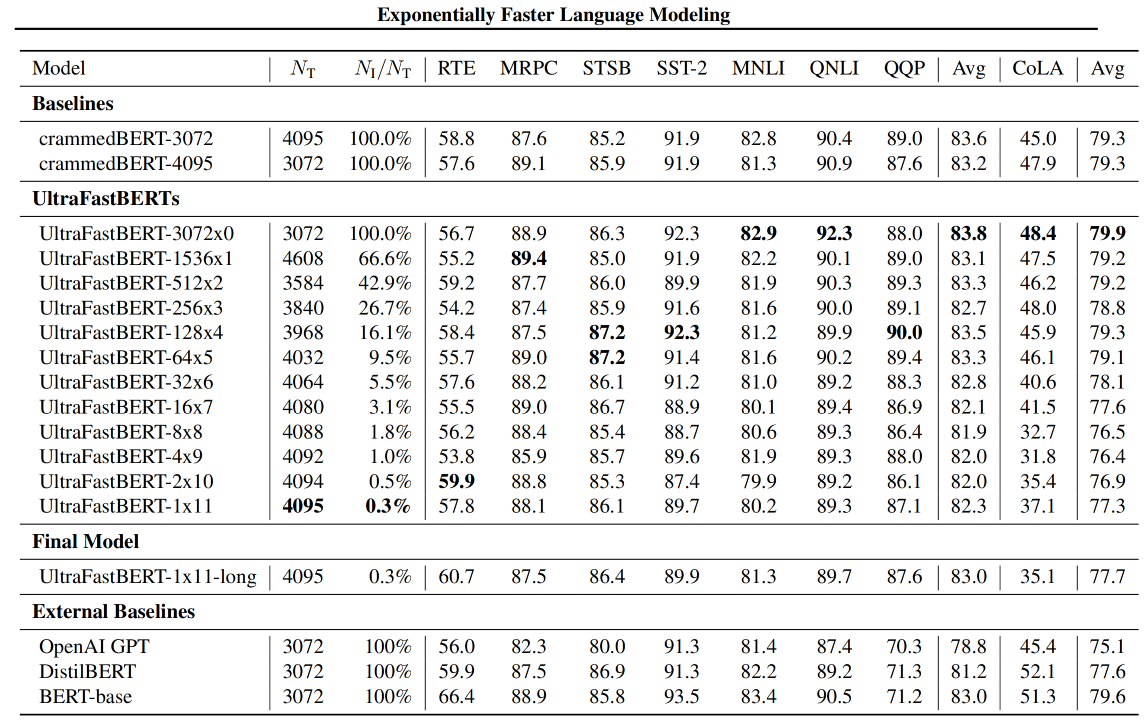
UltraFastBERT，一种BERT变体，在推理过程中使用0.3％的神经元，同时表现 与类似的BERT模型相当。UltraFastBERT选择性地使用4095个神经元中的12个（有选择的执行矩阵乘法（CMM））进行每层推理。这是通过用快速前馈网络(FFFs)取代前馈网络来实现的。

FFF_BMM代码

import torch
from torch import nn
import math

class FFF(nn.Module):
	def __init__(self, input_width: int, depth: int, output_width: int, *args, **kwargs):
		super().__init__(*args, **kwargs)

		self.input_width = input_width
		self.depth = depth
		self.output_width = output_width

		self.n_nodes = 2 ** (depth + 1) - 1
		self.initialise_weights()

	def initialise_weights(self):
		init_factor_l1 = 1.0 / math.sqrt(self.input_width)
		init_factor_l2 = 1.0 / math.sqrt(self.depth + 1)
		self.w1s = nn.Parameter(torch.empty(self.n_nodes, self.input_width).uniform_(-init_factor_l1, +init_factor_l1), requires_grad=True)
		self.w2s = nn.Parameter(torch.empty(self.n_nodes, self.output_width).uniform_(-init_factor_l2, +init_factor_l2), requires_grad=True)

	def forward(self, x):
		# the shape of x is (batch_size, input_width)
		# retrieve the indices of the relevant elements
		batch_size = x.shape[0]
		current_nodes = torch.zeros((batch_size,), dtype=torch.long, device=x.device)
		all_nodes = torch.zeros(batch_size, self.depth+1, dtype=torch.long, device=x.device)
		all_logits = torch.empty((batch_size, self.depth+1), dtype=torch.float, device=x.device)

		for i in range(self.depth+1):
			all_nodes[:, i] = current_nodes
			plane_coeffs = self.w1s.index_select(dim=0, index=current_nodes)			# (batch_size, input_width)
			plane_coeff_score = torch.bmm(x.unsqueeze(1), plane_coeffs.unsqueeze(-1))	# (batch_size, 1, 1)
			plane_score = plane_coeff_score.squeeze(-1).squeeze(-1) 					# (batch_size,)
			all_logits[:, i] = plane_score
			plane_choices = (plane_score >= 0).long()									# (batch_size,)

			current_nodes = current_nodes * 2 + plane_choices + 1						# (batch_size,)

		# get the weights
		selected_w2s = self.w2s.index_select(0, index=all_nodes.flatten()) \
			.view(batch_size, self.depth+1, self.output_width)	# (batch_size, depth+1, output_width)

		# forward pass
		mlp1 = torch.nn.functional.gelu(all_logits)				# (batch_size, depth+1)
		mlp2 = torch.bmm(mlp1.unsqueeze(1), selected_w2s) 		# (batch_size, output_width)
		
		# done
		return mlp2
	

从代码可以看出，与传统的批矩阵乘法(BMM)不同的是，在forward中，基于二叉树的结构，通过迭代计算节点的索引和权重，使用激活函数(GeLU)对结果进行处理，并最终得到输出。

结果

在推理过程中仅使用0.3％的神经元，同时表现与类似的BERT模型相当（下游任务没有降很多点）；实现78倍CPU加速，实现40倍PyTorch加速。

总结

该工作很有趣，将传统前馈神经网络定义成一棵二叉树，其叶子是小型神经网络，在每个非叶子节点处都有一个微小的神经网络（单个神经元也可以工作）来决定走哪条路径取决于在输入上。在训练期间，它们对所选路径进行加权平均值，从而得出树的所有叶子（在输入上评估为神经网络）的总加权平均值，但在推理过程中，它们可以只遵循投票最高的分支，从而得出建议的结果指数加速。并且，基于FFF的思想，将工作推到BERT这种语言模型上，初步证明了大模型的前馈层的神经元并不是都需要参与推理。

文章及公开的代码还介绍了条件矩阵乘法的详细细节，因此感兴趣可以深入研究一下。

参考文献

【1】paper：Exponentially Faster Language Modelling，https://arxiv.org/abs/2311.10770
【2】code：https://github.com/pbelcak/fastfeedforward
【3】paper：Fast Feedforward Networks，https://arxiv.org/abs/2308.14711

【4】code：https://github.com/pbelcak/UltraFastBERT
【5】model：https://huggingface.co/pbelcak/UltraFastBERT-1x11-long