代码随想录算法训练营第五十四天|392.判断子序列 115.不同的子序列

news2024/11/15 7:00:12

文档讲解：代码随想录

视频讲解：代码随想录B站账号

状态：看了视频题解和文章解析后做出来了

392.判断子序列

class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        dp = [[0] * (len(t)+1) for _ in range(len(s)+1)]

        for i in range(1, len(s) + 1):
            for j in range(1, len(t) + 1):
                if s[i-1] == t[j-1]:
                    dp[i][j] = dp[i-1][j-1] + 1
                else:
                    dp[i][j] = dp[i][j-1]
        
        return dp[len(s)][len(t)] == len(s)

时间复杂度：O(n^2)
空间复杂度：O(n)

1. 确定dp数组的含义

dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]

这里用i，j表示 i-1，j-1 是为了给初始化留一行和一列，而且递推公式也更方便。

2. 确定递推公式

第一种情况：s和j的元素相等，dp[i][j] 在 dp[i-1][j-1] 的基础上 + 1

第二种情况：s和j元素不相等，相当于要删除掉 j 的 i 位元素再去做对比，那就是 dp[i][j] = dp[i][j-1]

3. dp数组初始化

从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，所以dp[0][0]和dp[i][0]是一定要初始化的。

4. 确定遍历顺序

递推公式中的j是i和j之前的元素下标，所以从前往后递推。

5. 举例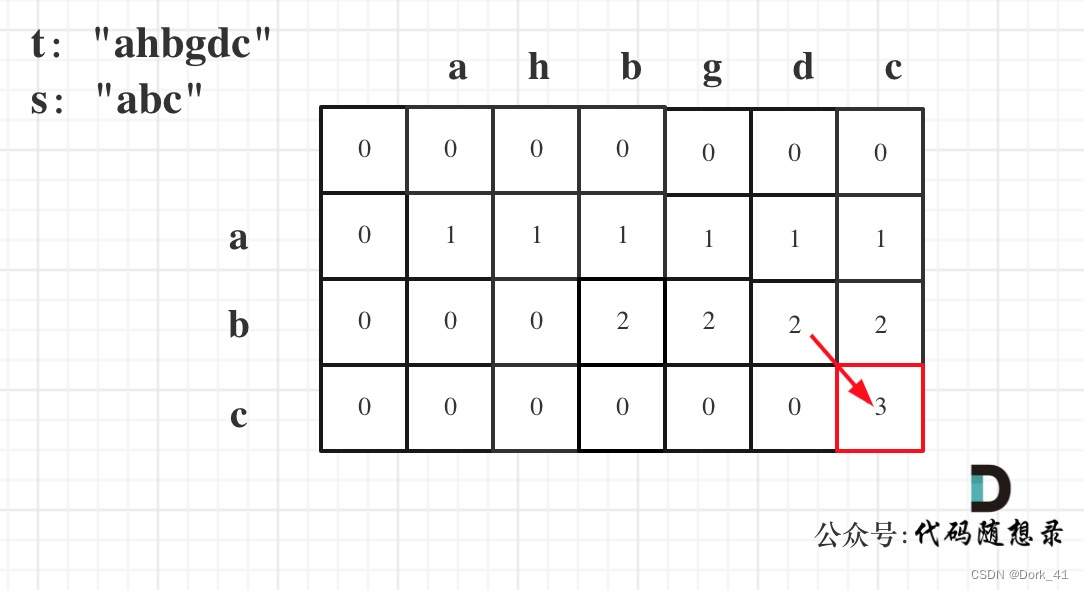

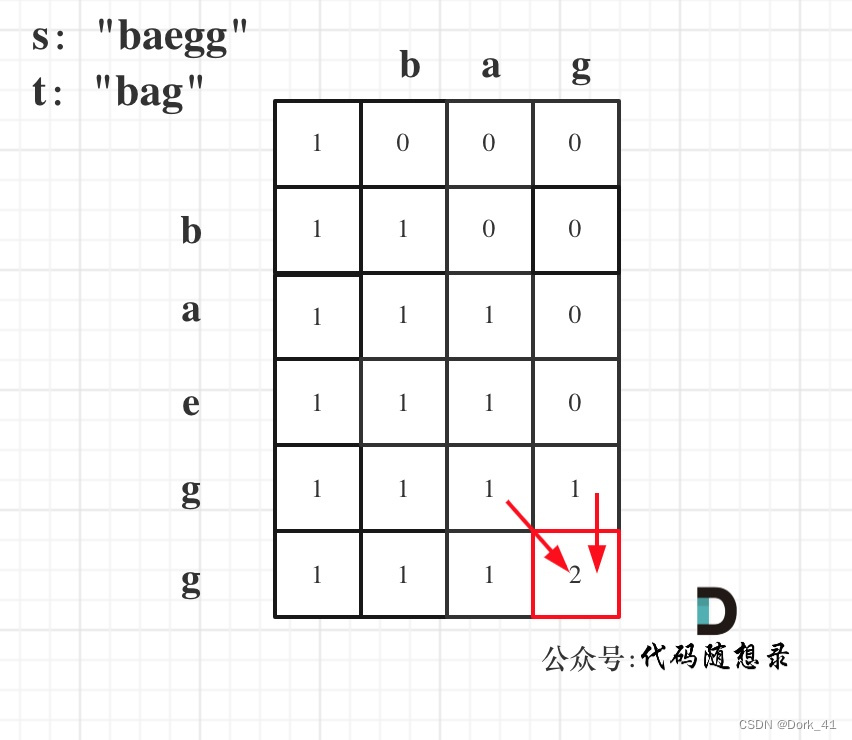
115.不同的子序列

class Solution:
    def numDistinct(self, s: str, t: str) -> int:
        dp = [[0] * (len(s) + 1) for _ in range(len(t) + 1)]

        for i in range(1, len(s) + 1):
            if t[0] == s[i-1]:
                dp[1][i] = dp[1][i-1] + 1
            else:
                dp[1][i] = dp[1][i-1]

        for i in range(2, len(t) + 1):
            for j in range(1, len(s) + 1):
                if t[i-1] == s[j-1]:
                    dp[i][j] = dp[i][j-1] + dp[i-1][j-1]
                else:
                    dp[i][j] = dp[i][j-1]

        return dp[-1][-1]